engineering-mathematics
Question 1 |

A | 19 |

Question 2 |

A | 10 |
B | 11 |
C | 9 |
D | 100 |
s(P,Q) is the sum of dot products of vectors P and Q in each dimension. The 0 dot product indicates that the vectors must be orthogonal to each other.
In a n-dimensional space, we have n axes orthogonal to each other. It is given that for every pair the dot product must be 0, then at most n vectors each mentioning each dimension can be considered. Thus for 10 dimensional space’s set of vectors ℒ , 10 mutually orthogonal vectors can be present.
Question 3 |
A | 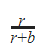 |
B |  |
C | 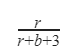 |
D | 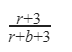 |
E |

-
There are 8 ways to get ‘red’ in the fourth attempt of drawing
i.e., _ _ _ R these three gaps can be filled with B/R in 222=8 ways
The probability for case (1),


Question 4 |
A | 59049 |

Question 5 |
A | 4 |
Question 6 |
- If the first question is answered wrong, the student gets zero marks.
- If the first question is answered correctly and the second question is not answered correctly, the student gets the marks only for the first question.
- If both the questions are answered correctly, the student gets the sum of the marks of the two questions.
| question | Probability of answering correctly | marks |
| QuesA QuesB | 0.8 0.5 | 10 20 |
A | First QuesB and then QuesA. Expected marks 22. |
B | First QuesA and then QuesB. Expected marks 16. |
C | First QuesA and then QuesB. Expected marks 14. |
D | First QuesB and then QuesA. Expected marks 14. |
There are two ways to get marks.
1. Answering first question correctly, and second one wrongly
2. Answering first question and second question correctly.
There are two ways to answer the question paper. First A or First B.
In total we get 4 ways of answering the paper to get marks.
Note: Answering each question is independent, thus P(x intersection y) = P(x)*P(y)|
P(Answering A correctly) =0.8, P( Answering A wrongly) = 1-0.8=0.2
P(Answering B correctly) =0.5, P( Answering B wrongly) = 1-0.5=0.5
|
Probability of Getting marks |
Marks |
|
|
First A correctly, B wrongly |
P(A correctly)*P(B wrongly) |
10+0 = 10 |
|
First A correctly B correctly |
P(A correctly)*P(B Correctly) |
10+20 = 30 |
|
First B correctly, A wrongly |
P(B correctly)*P(A wrongly) |
20+0=20 |
|
First B correctly then A correctly |
P(B correctly)*P(A Correctly) |
20+10=30 |
Expectation formula
E(X)=∑X*P(X)
Expectation for the order:A followed by B = 0.4*10 +0.4*30 = 16
Expectation for the order B followed by A = 0.1*20 + 0.4*30 = 14
As the target is to get maximum marks, the order A followed by B is the correct option
Question 7 |
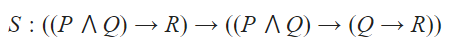
A | S is a contradiction. |
B | The anecdote of S is logically equivalent to the consequent of S. |
C | S is a tautology. |
D | S is neither a tautology nor a contradiction. |
Question 8 |

A | There exists a bijection from S1to S2. |
B | There does not exist a bijection from S1to S2. |
C | There exists a surjection from S1to S2. |
D | There does not exist an injunction from S1to S2. |
The number of functions from a set A to set B is |B|^|A|.
S2: |B|= 3, |A|= n^2-1 +1 = n^2.
we have number of functions 3^(n^2).
S1: there are n*n positions in a matrix of size nxn. Each can be filled with either 0 or 1 or 2 i,e, in 3^(n^2)
As there are equal number of elements on both sides, S1->S2 can be one one , onto as well bijection
Question 9 |
A | 15.49 |

Question 10 |
The probability that a number selected at random between 100 and 999 (both inclusive) will not contain the digit 7 is:
A | 16/25 |
B | (9/10)3 |
C | 27/75 |
D | 18/25 |
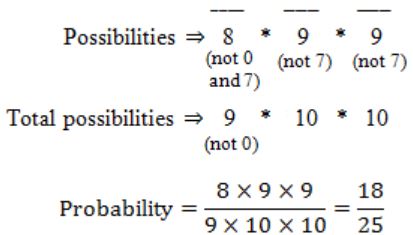
Question 11 |
Let R be a symmetric and transitive relation on a set A. Then
A | R is reflexive and hence an equivalence relation |
B | R is reflexive and hence a partial order
|
C | R is reflexive and hence not an equivalence relation |
D | None of the above |
i) Symmetric
ii) Reflexive
iii) Transitive
If a relation is said to be symmetric and transitive then we can't say the relation is reflexive and equivalence.
Question 12 |
The number of elements in he power set P (S) of the set S = {(φ), 1, (2, 3)} is:
A | 2 |
B | 4 |
C | 8 |
D | None of the above |
P(S) = {φ, {{φ}}, {1}, {{2, 3}}, {{φ}, 1}, {1, {2, 3}}, {{φ}, 1, {2, 3}}}
In P(S) it contains 8 elements.
Question 13 |
In the interval [0, π] the equation x = cos x has
A | No solution |
B | Exactly one solution |
C | Exactly two solutions |
D | An infinite number of solutions |
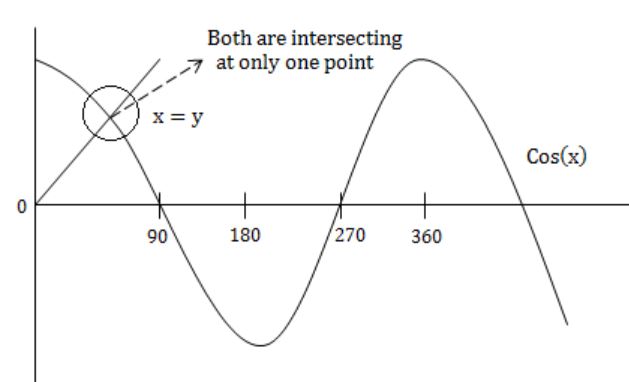
x & cos(x) are intersecting at only one point.
Question 14 |
If at every point of a certain curve, the slope of the tangent equals −2x/y the curve is
A | a straight line |
B | a parabola |
C | a circle |
D | an ellipse |
Question 15 |
The value of k for which 4x2 - 8xy + ky2 = 0 does not represent a pair of straight lines (both passing through the origin) is:
A | 0 |
B | 2 |
C | 9 |
D | 3 |
Question 16 |
The rank of the following (n + 1)×(n+1) matrix, where a is a real number is

A | 1 |
B | 2 |
C | n |
D | Depends on the value of a |

Question 17 |
The minimum number of edges in a connected cyclic graph on n vertices is:
A | n - 1 |
B | n |
C | n + 1 |
D | None of the above |
In cyclic graph:
No. of edges = No. of vertices
⇒ n = n
Question 18 |
If the cube roots of unity are 1, ω and ω2, then the roots of the following equation are (x - 1)3 + 8 = 0
A | -1, 1 + 2ω, 1 + 2ω2 |
B | 1, 1 - 2ω, 1 - 2ω2 |
C | -1, 1 - 2ω, 1 - 2ω2 |
D | -1, 1 + 2ω, -1 + 2ω2 |
Question 19 |
A language with string manipulation facilities uses the following operations
head(s): first character of a string tail(s): all but the first character of a string concat(s1,s2):s1 s2 for the string acbc what will be the output of concat(head(s), head(tail(tail(s))))
A | ac |
B | bc |
C | ab |
D | cc |
concat (a, head (tail (cbc)))
concat (a, head (bc))
concat (a, b)
ab
Question 20 |
A unit vector perpendicular to both the vectors a = 2i - 2j + k and b = 1 + j - 2k is:
A | 1/√3 (1+j+k) |
B | 1/3 (1+j-k) |
C | 1/3 (1-j-k) |
D | 1/√3 (1+j-k) |
E | None of the above. |

Question 21 |
A bag contains 10 white balls and 15 black balls. Two balls are drawn in succession. The probability that one of them is black and the other is white is:
A | 2/3 |
B | 4/5 |
C | 1/2 |
D | 2/1 |

Probability of first ball black and second one white is,
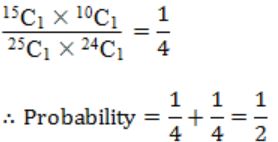
Question 22 |
The iteration formula to find the square root of a positive real number b using the Newton Raphson method is
A |  |
B | 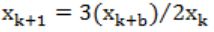 |
C | 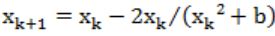 |
D | None of the above |
Question 23 |
Let A be the set of all non-singular matrices over real number and let* be the matrix multiplication operation. Then
A | A is closed under* but < A, *> is not a semigroup |
B | |
C | |
D |
Question 24 |
The solution of differential equation y'' + 3y' + 2y = 0 is of the form
A | C1ex + C2e2x |
B | C1e-x + C2e3x |
C | C1e-x + C2e-2x |
D | C1e-2x + C22-x |
Question 25 |
If the proposition ¬p ⇒ ν is true, then the truth value of the proposition ¬p ∨ (p ⇒ q), where ¬ is negation, ‘∨’ is inclusive or and ⇒ is implication, is
A | true |
B | multiple valued |
C | false |
D | cannot be determined |
So, either p or q must be True.
Now,
¬p ∨ (p → q)
= ¬p ∨ (¬p ∨ q)
= ¬p ∨ q
Since nothing c an be said about the truth values of p, it implies that ¬p ∨ q can also be True or False. Hence, the value cannot be determined.
Question 26 |
(a) Determine the number of divisors of 600.
(b) Compute without using power series expansion ![]()
A | Theory Explanation. |
Question 27 |
Obtain the principal (canonical) conjunctive normal form of the propositional formula
(p ∧ q) V (¬q ∧ r)
Where ‘∧’ is logical and, ‘v’ is inclusive or and ¬ is negation.
A | Theory Explanation. |
Question 28 |
Let G1 and G2 be subgroups of a group G.
(a) Show that G1 ∩ G2 is also a group of G.
(b) Is G1 ∪ G2 always a subgroup of G?
A | Theory Explanation. |
Question 29 |
Prove using mathematical induction for n≥5, 2n > n2
A | Theory Explanation. |
Question 30 |
Prove that in finite graph, the number of vertices of odd degree is always even.
A | Theory Explanation. |
Question 31 |
(a) Find the minimum value of 3 - 4x + 2x2.
(b) Determine the number of positive integers (≤ 720) which are not divisible by
any of numbers 2, 3, and 5.
A | Theory Explanation. |
Question 32 |
Let G be a group of 35 elements. Then the largest possible size of a subgroup of G other than G itself is ______.
A | 7 |
If ‘H” is a subgroup of finite group (G,*) then O(H) is the divisor of O(G).
Given that the order of group is 35. Its divisors are 1,5,7,35.
It is asked that the size of largest possible subgroup other than G itself will be 7.
Question 33 |
Let R be the set of all binary relations on the set {1,2,3}. Suppose a relation is chosen from R at random. The probability that the chosen relation is reflexive (round off to 3 decimal places) is _____.
A | 0.125 |
The number of reflexive relations is 2^(n^2-n).
The total number of relations on a set with n elements is 2^ (n^2).
The probability of choosing the reflexive relation out of set of relations is
= 2^(n^2-n) /2^ (n^2)
= 2^( n^2-n- n^2)
= 2^(-n)
Given n=3, the probability will be 2-n = ⅛ = 0.125
Question 34 |
Consider the functions
- I. e-x
II. x2-sin x
III. √(x3+1)
Which of the above functions is/are increasing everywhere in [0,1]?
A | II and III only |
B | III only |
C | II only |
D | I and III only |
I. e-x
II. f'(x) = -e-x
f'(x)<0 on the interval [0,1] so this is not an increasing function.
II. x2-sinx
f'(x) = 2x - cosx
at x=0, f'(0) = 2(0) - 1 = -1 < 0
f(x) = x2 - sinx is decreasing over some interval, increasing over some interval as cosx is periodic.
As the question is asked about increasing everywhere II is false.
III. √(x3+1) = (x3+1)1/2
f'(x) = 1/2(3x2/√(x3+1))>0
f(x) is increasing over [0,1].
Question 35 |
For n>2, let a ∈ {0,1}n be a non-zero vector. Suppose that x is chosen uniformly at random from {0,1}n. Then, the probability that is an odd number ![]() is _____.
is _____.
A | 0.5 |
‘x’ is a vector chosen randomly from {0,1}n
‘a’ can have 2(n-1) possibilities, x can have 2n possibilities.
∑aixi have (2n-1)(2n) possibilities, which is an even number of outcomes.
The probability of https://solutionsadda.in/wp-content/uploads/2020/02/41.jpg is odd is ½.
For example:
Take n=3
a = {001, 010, 100, 011, 101, 111}
x = {000, 001, 010, 011, 100, 101, 110, 111}
Computed as [001]×[000] = 0+0+0 = 0 Output = even
[001]×[001] = 0+0+1 = 0 Output = odd
Similarly, there could be 28 even, 28 odd outputs for the a(size=7), x(size=8) of total 56 outputs.
Question 36 |
Graph G is obtained by adding vertex s to K3,4 and making s adjacent to every vertex of K3,4. The minimum number of colours required to edge-colour G is _____.
A | 7 |
The vertex in the set of size 3 has 4 edges connected to 4 vertices on other set. So, edge color of G is max(3,4) i.e. 4.
When a vertex is added to the graph with 7 vertices ( K3x4 has 7 vertices), there would be 7 edges associated to that new vertex. As per the edge coloring “no two adjacent edges have same color).
As the new vertex with 7 edges need to be colored with 7 colors, the edge color of graph G is 7.
Question 37 |
Which one of the following predicate formulae is NOT logically valid?
Note that W is a predicate formula without any free occurrence of x.
A | ∃x(p(x) → W) ≡ ∀x p(x) → W |
B | ∀x(p(x) → W) ≡ ∀x p(x) → W
|
C | ∃x(p(x) ∧ W) ≡ ∃x p(x) ∧ W |
D | ∀x(p(x) ∨ W) ≡ ∀x p(x) ∨ W |
~p→q ≡ ~p∨q
Demorgan laws:
~(∀x(a(x)) ≡ ∃x~a(x)
~(∃x(a(x)) ≡ ∀x~a(x)
(A) ∃x(p(x)→w) ≡ ∀x p(x)→w
LHS: ∃x(p(x)→w) ≡ ∃x(~p(x)∨w)
≡ ∃x(~p(x))∨w
Demorgan’s law:
~(∀x(a(x)) = ∃x ~ a(x)
≡ ~(∀x P(x)) ∨ w
≡ (∀x) P(x) → w ≡ RHS
It’s valid.
(B) ∀x(P(x) → w) ≡ ∀x(~P(x) ∨ w)
≡ ∀x(~P(x)) ∨ w
≡ ~(∃x P(x)) ∨ w
≡ ∃x P(x) → w
This is not equal to RHS.
(C) ∃x(P(x) ∧ w) ≡ ∃x P(x) ∧ w
‘w’ is not a term which contains x.
So the quantifier does not have any impact on ‘w’.
Thus it can be written as
∃x(P(x)) ∧ w) ≡ ∃x P(x) ∧ w
(D) ∀(x)(P(x) ∨ w) ≡ ∀x P(x) ∨ w
‘w’ is not a term which contains ‘x’.
So the quantifier does not have an impact on ‘w’.
Thus ∀(x)(P(x) ∨ w) ≡ ∀x P(x) ∨ w
Question 38 |
The number of permutations of the characters in LILAC so that no character appears in its original position, if the two L’s are indistinguishable, is _______.
A | 12 |
― ― ― ― ―
Given: L I L A C
The derangement formula ⎣n!/e⎦ cannot be directly performed as there are repeated characters.
Let’s proceed in regular manner:
The L, L can be placed in other ‘3’ places as
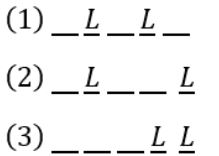
(1) Can be arranged such that A, I, C be placed in three positions excluding ‘C’ being placed at its own position, which we get only 2×2×1 = 4 ways.
Similarly (2) can be filled as A, I, C being placed such that 4th position is not filled by A, so we have 2×2×1 = 4 ways. Similarly with (3).
Totally, we get 4+4+4 = 12 ways.
Question 39 |
Let A and B be two n×n matrices over real numbers. Let rank(M) and det(M) denote the rank and determinant of a matrix M, respectively. Consider the following statements,
- I. rank(AB) = rank(A) rank(B)
II. det(AB) = det(A) det(B)
III. rank(A + B) ≤ rank(A) + rank(B)
IV. det(A + B) ≤ det(A) + det(B)
Which of the above statements are TRUE?
A | I and II only
|
B | I and IV only |
C | III and IV only |
D | II and III only
|
Rank is the number of independent rows(vectors) of a matrix. On product of two matrices, the combined rank is more than the sum of individual matrices (subtracted with the order n)
det(AB) = det(A)∙det(B) as the magnitude remains same for the matrices after multiplication.
Note: We can just take a 2x2 matrix and check the options.
Question 40 |
Let A and B be sets and let Ac and Bc denote the complements of the sets A and B. The set (A – B) ∪ (B - A) ∪ (A∩B) is equal to
A | A ∪ B |
B | Ac ∪ Bc |
C | A ∩ B |
D | Ac ∩ Bc |
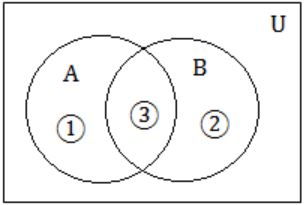
(A - B) = 1
(B - A) = 2
(A∩B) = 3
A∪B = (1∪2∪3)
(A – B) ∪ (B - A) ∪ (A∩B) = 1∪2∪3 = (A∪B)
Question 41 |
Let X = {2,3,6,12,24}, Let ≤ be the partial order defined by X ≤ Y if x divides y. Number of edge as in the Hasse diagram of (X,≤) is
A | 3 |
B | 4 |
C | 9 |
D | None of the above |
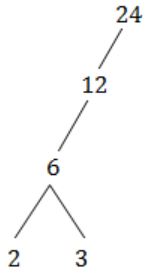
No. of edges = 4
Question 42 |
Suppose X and Y are sets and X Y and are their respective cardinalities. It is given that there are exactly 97 functions from X to Y. from this one can conclude that
A | |X| = 1, |Y| = 97 |
B | |X| = 97, |Y| = 1 |
C | |X| = 97, |Y| = 97 |
D | None of the above |
|Y||X| = 97
→ Option A only satisfies.
Question 43 |
Which of the following statements is false?
A | The set of rational numbers is an abelian group under addition. |
B | The set of integers in an abelian group under addition. |
C | The set of rational numbers form an abelian group under multiplication. |
D | The set of real numbers excluding zero in an abelian group under multiplication. |
Question 44 |
Two dice are thrown simultaneously. The probability that at least one of them will have 6 facing up is
A | 1/36 |
B | 1/3 |
C | 25/36 |
D | 11/36 |
1 - (5/6 × 5/6) = 1 - (25/36) = 11/36
Question 45 |
The formula used to compute an approximation for the second derivative of a function f at a point X0 is
A | f(x0+h) + f(x0-h)/2 |
B | f(x0+h) - f(x0-h)/2h |
C | f(x0+h) + 2f(x0) + f(x0-h)/h2 |
D | f(x0+h) - 2f(x0) + f(x0-h)/h2 |
f(x0+h) - 2f(x0) + f(x0-h)/h2
Question 46 |
Let Ax = b be a system of linear equations where A is an m × n matrix and b is a m × 1 column vector and X is a n × 1 column vector of unknowns. Which of the following is false?
A | The system has a solution if and only if, both A and the augmented matrix [A b] have the same rank.
|
B | If m < n and b is the zero vector, then the system has infinitely many solutions. |
C | If m = n and b is non-zero vector, then the system has a unique solution. |
D | The system will have only a trivial solution when m = n, b is the zero vector and rank (A) = n. |
→ Solution can be depends on rank of matrix A and matrix [A B].
→ If rank[A] = rank[A B] then it can have solution otherwise no solution.
Question 47 |
Let R denotes the set of real numbers. Let f: R×R → R×R be a bijective function defined by f(x,y) = (x+y,x-y), The inverse function of f is given by
A | 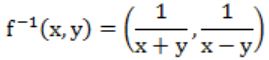 |
B | 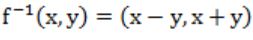 |
C | 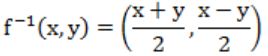 |
D | 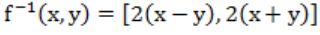 |
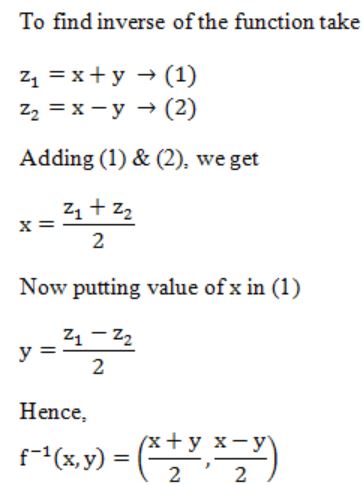
Question 48 |
Let R be a non-empty relation on a collection of sets defined by A R B if and only if A ∩ B = ф. Then, (pick the true statement)
A | R is reflexive and transitive |
B | R is symmetric and not transitive |
C | R is an equivalence relation |
D | R is not reflexive and not symmetric |
Now,
A ∩ B = ф
& B ∩ C = ф
But A ∩ B ≠ ф
So, R is not transitive.
A ∩ B = A, so R is not reflexive.
If A ∩ B = ф
then definitely B ∩ A = ф.
Hence, R is symmetric.
So, option (B) is true.
Question 49 |
Which of the following is false? Read ∧ as AND, ∨ as OR, ~ as NOT, → as one way implication and ↔ as two way implication.
A | ((x → y) ∧ x) → y |
B | ((x → y) ∧ (x ∧ y)) → x |
C | (x → (x ∨ ψ)) |
D | ((x ∨ y) ↔ (x → y) |
then option (D) will be False.
Question 50 |
Which one of the following is false?
A | The set of all bijective functions on a finite set forms a group under function composition.
|
B | The set {1, 2, ……., p–1} forms a group under multiplication mod p where p is a prime number. |
C | The set of all strings over a finite alphabet forms a group under concatenation. |
D | A subset s ≠ ф of G is a subgroup of the group |
