Graph-Theory
Question 1 |
The minimum number of edges in a connected cyclic graph on n vertices is:
n - 1 | |
n | |
n + 1 | |
None of the above |
In cyclic graph:
No. of edges = No. of vertices
⇒ n = n
Question 2 |
Prove that in finite graph, the number of vertices of odd degree is always even.
Theory Explanation. |
Question 3 |
Graph G is obtained by adding vertex s to K3,4 and making s adjacent to every vertex of K3,4. The minimum number of colours required to edge-colour G is _____.
7 |
The vertex in the set of size 3 has 4 edges connected to 4 vertices on other set. So, edge color of G is max(3,4) i.e. 4.
When a vertex is added to the graph with 7 vertices ( K3x4 has 7 vertices), there would be 7 edges associated to that new vertex. As per the edge coloring “no two adjacent edges have same color).
As the new vertex with 7 edges need to be colored with 7 colors, the edge color of graph G is 7.
Question 4 |
Let G be a graph with 100 vertices numbered 1 to 100. Two vertices i and j are adjacent if |i - j| = 8 or |i - j| = 12. The number of connected components in G is
8 | |
4 | |
12 | |
25 |
1 — 9 — 17 — ......... — 97
2 — 10 — 18 — ......... — 98
3 — 11 — 19 — ......... — 99
4 — 12 — 20 — ......... — 100
5 — 13 — 21 — ......... — 93
6 — 14 — 22 — ......... — 94
7 — 15 — 23 — ......... — 95
8 — 16 — 24 — ......... — 96
We have covered all vertices using 8 vertex sets considering only |i - j| = 8. Using |i - j| = 12 we can see the vertex 1 is connected to 13, 2 to 14, 3 to 15 and 4 to 16. So the top 4 vertex sets are infact connected to the bottom 4 sets, thus reducing the connected components to 4.
Question 5 |
The chromatic number of the following graph is _______.
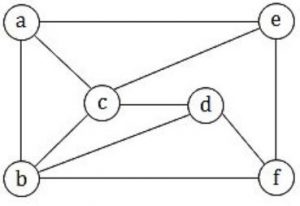
1 | |
2 | |
3 | |
4 |
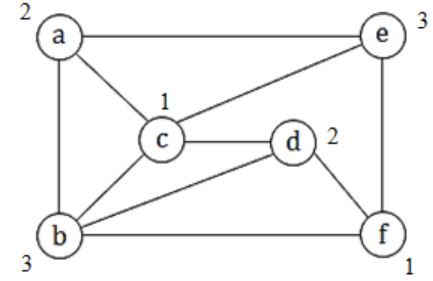
Question 6 |
Let G be a graph with 100! vertices, with each vertex labeled by a distinct permutation of the numbers 1, 2, …, 100. There is an edge between vertices u and v if and only if the label of u can be obtained by swapping two adjacent numbers in the label of v. Let y denote the degree of a vertex in G, and z denote the number of connected components in G.
Then, y + 10z = ___________.
109 | |
110 | |
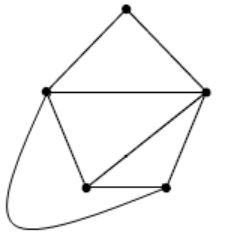
111 | |
112 |
There exists edge between two vertices iff label of ‘u’ is obtained by swapping two adjacent numbers in label of ‘v’.
Example:
12 & 21, 23 & 34
The sets of the swapping numbers be (1, 2) (2, 3) (3, 4) … (99).
The no. of such sets are 99 i.e., no. of edges = 99.
As this is regular, each vertex has ‘99’ edges correspond to it.
So degree of each vertex = 99 = y.
As the vertices are connected together, the number of components formed = 1 = z
y + 102 = 99 + 10(1) = 109
Question 7 |
(a) Prove by induction that the expression for the number of diagonals in a polygon of n sides is n(n-3)/2.
(b) Let R be a binary relation on A = {a, b, c, d, e, f, g, h} represented by following two component digraph. Find the smallest integers m and n such that mm = Rn.
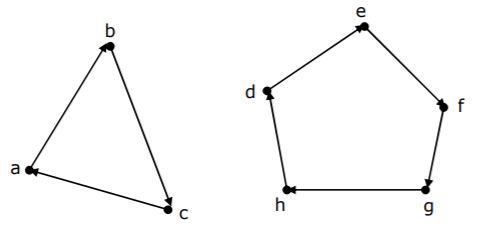
Theory Explanation. |
Question 8 |
Let (A, *) be a semi group. Furthermore, for every a and b in A, if a ≠ b, then a*b ≠ b*a.
(a) Show that for every a in A
a*a = a
(b) Show that for every a, b in A
a*b*a = a
(c) Show that for every a, b, c in A
a*b*c = a*c
Theory Explanation. |
Question 9 |
Let G be a connected, undirected graph. A cut in G is a set of edges whose removal results in 0 being broken into two or more components which are not connected with each other. The size of a cut is called its cardinality. A men-cut of G is a cut in G of minimum cardinality. Consider the following graph.

(a) Which of the following sets of edges is a cut?
(i) {(A,B), (E,F), (B,D), (A,E), (A,D)}
(ii) {(B,D), (C,F), (A,B)}
(b) What is the cardinality of a min-cut in the graph?
(c) Prove that if a connected undirected graph G with n vertices has a min-cut of cardinality K, then G has atleast (nk/2) edges.
Theory Explanation. |
Question 10 |
Let S be a set of n elements {1, 2, …., n} and G a graph with 2n vertices, each vertex corresponding to a distinct subset of S. Two vertices are adjacent iff the symmetric difference of the corresponding sets has exactly 2 elements. Note: The symmetric difference of two sets R1 and R2 is defined as (R1/R2)∪(R2/R1)
(a) Every vertex in G has the same degree. What is the degree of a vertex in G?
(b) How many connected components does G have?
Theory Explanation is given below. |
Question 11 |
How many undirected graphs (not necessarily connected) can be constructed out of a given set V = {v1, v2, ...,vn} of n vertices?
n(n-1)/2 | |
2n | |
n! | |
2n(n-1)/2 |
Each subset of these edges will be form a graph.
No. of possible undirected graphs is 2(n C 2)
⇒ 2(n(n-1)/2)
Question 12 |
The minimum number of colours required to colour the vertices of a cycle with η nodes in such a way that no two adjacent nodes have the same colour is
2 | |
3 | |
4 | |
n - 2[n/2] + 2 |
Question 13 |
Maximum number of edges in a n-node undirected graph without self loops is
n2 | |
n(n-1)/2 | |
n-1 | |
(n+1)(n)/2 |
Question 14 |
Let G be an arbitrary graph with n nodes and k components. If a vertex is removed from G, the number of components in the resultant graph must necessarily lie between
k and n | |
k – 1 and k + 1 | |
k – 1 and n – 1 | |
k + 1 and n – k |
If a vertex is removed then it results that all the components are also be disconnected. So removal can create (n-1) components.
Question 15 |
How many perfect matching are there in a complete graph of 6 vertices ?
15 | |
24 | |
30 | |
60 |
(2n)!/n!×2n
Given, 2n = 6 ⇒ n = 3
So, finally, 6!/3!×23 = 15
Question 16 |
A graph G = (V,E) satisfies |E|≤ 3|V|-6. The min-degree of G is defined as ![]() . Therefore, min-degree of G cannot be
. Therefore, min-degree of G cannot be
3 | |
4 | |
5 | |
6 |
|E| ≤ 3|v| - 6
Based on handshaking lemma, the minimum degree is (min×|v|)/2
⇒ (min×|v|)/2 ≤ 3|v| - 6
Checking the options lets take min=6
(6×|v|)/2 ≤ 3|v| - 6
0 ≤ -6 (Not satisfied)
And which is inconsistent.
Question 17 |
The minimum number of colours required to colour the following graph, such that no two adjacent vertices are assigned the same colour, is
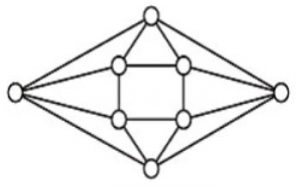
2 | |
3 | |
4 | |
5 |
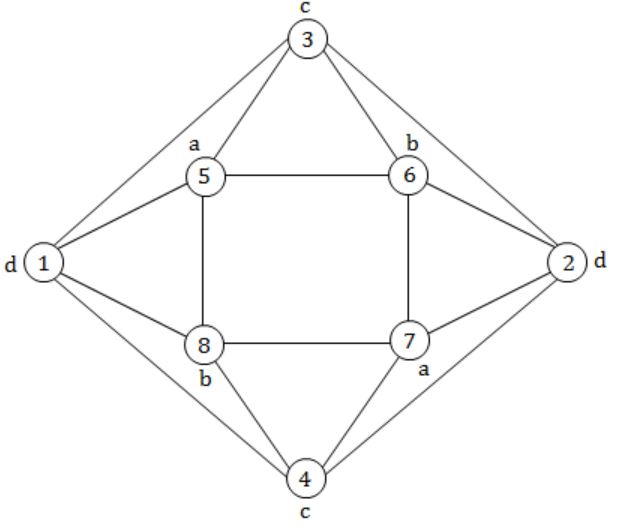
→ a, b, c, d = 4
→ The minimum no. of colours required to colour a graph = 4 (no two adjacent vertices have same colours)
Question 18 |
How many graphs on n labeled vertices exist which have at least (n2 - 3n)/2 edges?
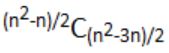 | |
 | |
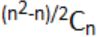 | |
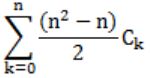 |
Maximum no. of vertices = n(n-1)/2 = v
No. of graphs with minimum b edges is
= C(v,e) + C(v,e+1) + C(v,e+2) + ... + C(v,v)
= C((v,v-e) + C(v,v-(e+1)) + C(v,v-(e+2)) + ... + C(v,0)
= C(a,n) + C(a,n-1) + C(a,n-2) + ... + C(a,0) (since a-b=n)
= C(n(n-1)/2,n) + C(n(n-1)/2,n-1) + ... + C(n(n-1)/2,0)
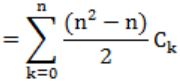
Question 19 |
Let G1 = (V,E1) and G2 = (V,E2) be connected graphs on the same vertex set V with more than two vertices. If G1 ∩ G2 = (V, E1 ∩ E2) is not a connected graph, then the graph G1 U G2 = (V, E1 U E2)
cannot have a cut vertex
| |
must have a cycle | |
must have a cut-edge (bridge)
| |
has chromatic number strictly greater than those of G1 and G2
|
(A)
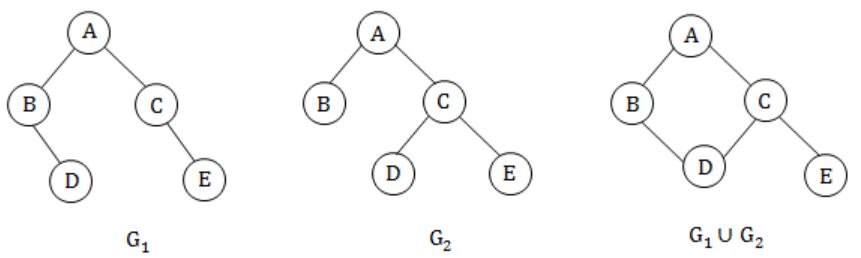
False, since in G1∪G2 'C' is a cut vertex.
(B) True, for all conditions.
(C)

False. G1∪G2 has no bridge.
D)

False. G1∪G2, G1, G2 all the three graphs have chromatic number of 2.
Question 20 |
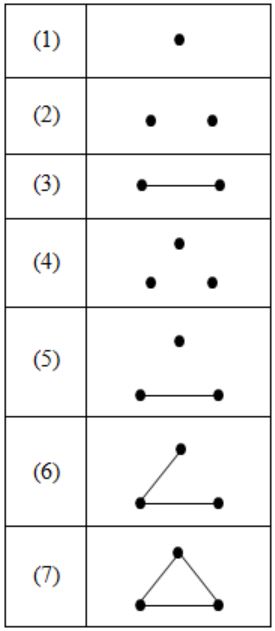
The number of distinct simple graphs with upto three nodes is
15 | |
10 | |
7 | |
9 |
Question 21 |
The number of edges in a regular graph of degree d and n vertices is _________.
d*n/2 |
d * n = 2 * |E|
∴ |E| = d*n/2
Question 22 |
Maximum number of edges in a planar graph with n vertices is ________
3n - 6 |
⇒ (3n - 2) = 3n - 6
Question 23 |
A non-planar graph with minimum number of vertices has
9 edges, 6 vertices | |
6 edges, 4 vertices | |
10 edges, 5 vertices | |
9 edges, 5 vertices |

The above graph with 5 vertices and 10 edges is non-planar.
Question 24 |
Let T be a Depth First Tree of a undirected graph G. An array P indexed by vertices of G is given. P[V] is the parent of vertex V, in T. Parent of the root is the root itself.
Give a method for finding and printing the cycle formed if the edge (u,v) of G not in T (i.e., e ∈ G − T) is now added to T.
Time taken by your method must be proportional to the length of the cycle.
Describe the algorithm in a PASCAL – like language. Assume that the variables have been suitably declared.
Theory Explanation. |
Question 25 |
(a) If G is a group of even order, then show that there exists an element a ≠ e, the identity in g, such that a2 = e
(b) Consider the set of integers {1,2,3, 4,6,8,12,24} together with the two binary operations LCM (lowest common multiple) and GCD (greatest common divisor). Which of the following algebraic structures does this represent?
(i) group (ii) ring (iii) field (iv) lattice
Theory Explanation. |
Question 26 |
36 |
Given 10 vertices,
Then we can have a complete graph with 9 vertices and one isolated verted.
Number of edges in complete graph with 9 edges is n(n-1)/2 = 9*8/2 = 36
Question 27 |
A ^3 | |
A^ 3 divided by 2 | |
A ^3 divided by 3 | |
A ^3 divided by 6 |
Question 28 |

Which of the following statements is/are TRUE?
The chromatic number of the graph is 3. | |
The graph has a Hamiltonian path | |
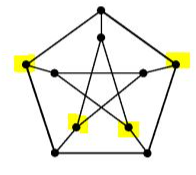
The following graph is isomorphic to the Peterson graph. 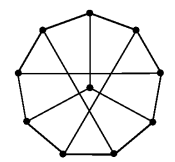 | |
The size of the largest independent set of the given graph is 3. (A subset of vertices of a graph form an independent set if no two vertices of the subset are adjacent.) |
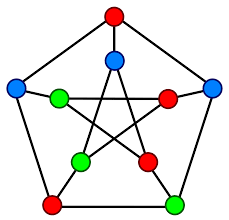
Peterson graph ihas hamiltonian path but not hamiltonian cycle
Given graph in option C is isomorphic as the given has same number of vertice, edges, degree sequence and cycles.
LArgest independent set can be more than 3
Question 29 |
The diagonal entries of A 2 are the degrees of the vertices of the graph. | |
If the graph is connected, then none of the entries of A^ n + 1 + I n can be zero. | |
If the sum of all the elements of A is at most 2( n- 1), then the graph must be acyclic. | |
If there is at least a 1 in each of A ’s rows and columns, then the graph must be Connected. |
The entries aii show the number of 2-length paths between the nodes i and j. Why this happens is easy to see: if there is an edge ij and an edge jk, then there will be a path ik through j. The entries ii are the degrees of the nodes i.
Similarly in A^3 we have the entries aii that show the number of 3-length paths between the nodes i and j.
In A^n-1 + I n, we will have at least n-1 length paths, so there is no possibility of zero entires
Question 30 |
11 |
v - e + f = 2
v is number of vertices
e is number of edges
f is number of faces including bounded and unbounded
8-e+5=2
=> 13-2 =e
The number of edges are =11
Question 31 |

Let M be the adjacency matrix of G.
Define graph G2on the same set of vertices with adjacency matrix N, where

Which one of the following statements is true?
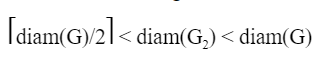 | |
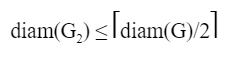 | |
 | |
 |



Question 32 |
What is the maximum number of edges in an acyclic undirected graph with n vertices?
n - 1 | |
n | |
n + 1 | |
2n - 1 |
= n - 1
Question 33 |
What is the number of vertices in an undirected connected graph with 27 edges, 6 vertices of degree 2, 3 vertices of degree 4 and remaining of degree 3?
10 | |
11 | |
18 | |
19 |
By Handshaking Lemma,
6 * 2 + 3 * 4 + (x - 9) * 3 = 27 * 2
24 + (x - 9) * 3 = 54
x = 19
Question 34 |
Let G be a weighted undirected graph and e be an edge with maximum weight in G. Suppose there is a minimum weight spanning tree in G containing the edge e. Which of the following statements is always TRUE?
There exists a cutset in G having all edges of maximum weight | |
There exists a cycle in G having all edges of maximum weight | |
Edge e cannot be contained in a cycle | |
All edges in G have the same weight |
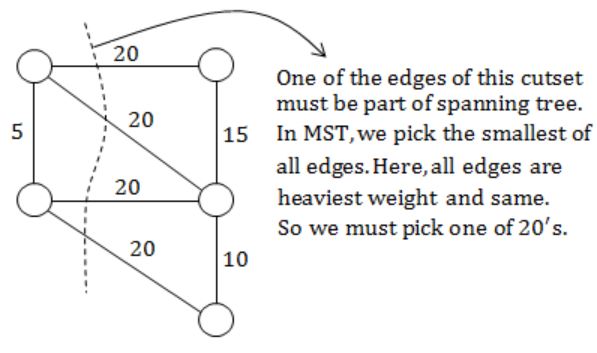
(B) False, because the cutset of heaviest edge may contain only one edge.
(C) False. The cutset may form cycle with other edge.
(D) False. Not always true.
Question 35 |
Let G be a directed graph whose vertex set is the set of numbers from 1 to 100. There is an edge from a vertex i to a vertex j iff either j = i + 1 or j = 3i. The minimum number of edges in a path in G from vertex 1 to vertex 100 is
4 | |
7 | |
23 | |
99 |
j = i +1
(or)
j = 3i
Second option will help us reach from 1 to 100 rapidly. The trick to solve this question is to think in reverse way. Instead of finding a path from 1 to 100, try to find a path from 100 to 1.
So, the edge sequence with minimum number of edges is
1 → 3 → 9 → 10 → 11 → 33 → 99 → 100
which consists of 7 edges.
Question 36 |
Consider the undirected graph G defined as follows. The vertices of G are bit strings of length n. We have an edge between vertex u and vertex v if and only if u and v differ in exactly one bit position (in other words, v can be obtained from u by flipping a single bit). The ratio of the chromatic number of G to the diameter of G is
1/(2n-1) | |
1/n | |
2/n | |
3/n |
That will give us a bipartite graph, with chromatic number = 2
Also from the same we can conclude that we need for a 'n' bit string, to traverse no more than (n-1) edges or 'n' vertices to get a path between two arbitrary points. So the ratio is (2/n).
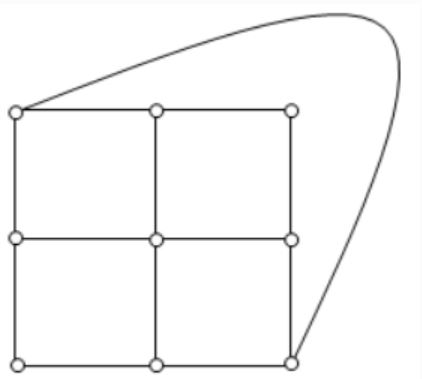
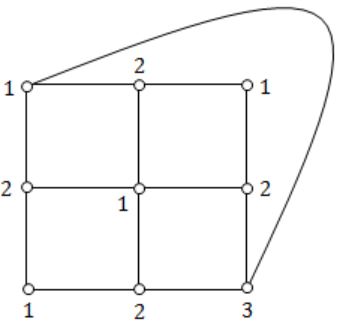
Question 37 |
What is the chromatic number of the following graph?
2 | |
3 | |
4 | |
5 |
→ Chromatic number of a graph is the smallest number of colours needed to colour the vertices so that no two adjacent vertices share the same colour.
Question 38 |
What is the size of the smallest MIS(Maximal Independent Set) of a chain of nine nodes?
5 | |
4 | |
3 | |
2 |
(2, 5, 8) is the maximal independent set for a chain of 9 nodes. If we add any start node to the set then it will not be MIS.
Independent set:
A set of vertices is called independent set such that no two vertices in the set are adjacent.
Question 39 |
G is a simple undirected graph. Some vertices of G are of odd degree. Add a node v to G and make it adjacent to each odd degree vertex of G. The resultant graph is sure to be
Regular | |
Complete | |
Hamiltonian | |
Euler |
→ In Euler graph all degrees must be even for all nodes. And number of odd degree vertices should be even.
→ So, degree of this new node will be even and as a new edge is formed between this new node and all other nodes of odd degree hence here is not a single node exists with degree odd so this is Euler graph.
Question 40 |
Which of the following graphs is/are planner?
Theory Explanation is given below. |
→ Let us assume K33is a planar graph. Then it satisfy the useful corollary. As there is no triangle in K33.
Let G be a connected planar graph with n vertices and m edges, and no triangles. Then m≤2n-4.
Where m=9, n=6
⇒ 9 ≤ 12 - 4
⇒ 9 ≤ 8, which is to be false, then K33 is non-planar graph.
(ii) G2 is a planar graph. Because it can be redrawn like as below.
(iii) Let us assume G3 be a planar graph then it also be satisfy useful corollary.
Where m=9, n=6
then 9 ≤ 12-4
9 ≤ 8 is False
So, G3 is non-planar graph.
Answer: Only G2 is planar graph.
Question 41 |
The maximum number of possible edges in an undirected graph with a vertices and k components is ________.
(n-k)(n-k+1)/2 |
To get maximum, take one vertex each for each component, except last component.
Now, k-1 components have 1 vertex each and so on edges.
The last component has (n-(k-1)) vertices. So make the last component complete, i.e., it has n-(n-1)C2
= (n-k)(n-k+1)/2
= maximum no. of edges
Question 42 |
Choose the correct alternatives (More than one may be correct).
A graph is planar if and only if,It does not contain subgraphs homeomorphic to k5 and k3,3. | |
It does not contain subgraphs isomorphic to k5 or k3,3. | |
It does not contain a subgraph isomorphic to k5 or k3,3. | |
It does not contain a subgraph homeomorphic to k5 or k3,3. |
Question 43 |
Let G be a simple connected planar graph with 13 vertices and 19 edges. Then, the number of faces in the planar embedding of the graph is:
6 | |
8 | |
9 | |
13 |
F = E - V + 2 [From Euler's formula i.e., F + V - E = 2]
F = 19 - 13 +2
F = 8
Question 44 |
Let G be a simple graph with 20 vertices and 100 edges. The size of the minimum vertex cover of G is 8. Then, the size of the maximum independent set of G is
12 | |
8 | |
Less than 8 | |
More than 12
|
Edges = 100
Minimum cover of vertex G is = 8
Maximum Independent set of G = No. of vertices - Minimum cover of vertex G
= 20 - 8
= 12
Question 45 |
Which one of the following graphs is NOT planar?
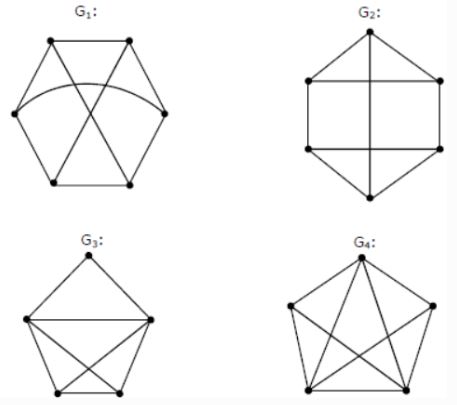
G1 | |
G2 | |
G3 | |
G4 |
which is planar
G3 can also be drawn as
which is planar
G4 can also be drawn as

which is planar
But G1 cannot be drawn as planar graph.
Hence, option (A) is the answer.
Question 46 |
G is an undirected graph with n vertices and 25 edges such that each vertex of G has degree at least 3. Then the maximum possible value of n is ___________.
16 | |
17 | |
18 | |
19 |
Degree of each vertex ≥ 3

|v| = 2|E|
The relation between max and min degree of graph are
m ≤ 2|E| / |v| ≤ M
Given minimum degree = 3
So, 3 ≤2 |E| / |v|
3|v| ≤ 2|E|
3(n) ≤ 2(25)
n ≤ 50/3
n ≤ 16.6
(n = 16)
Question 47 |
G contains a complete subgraph with k vertices
| |
G contains an independent set of size at least n/k
| |
G contains at least k(k−1)/2 edges | |
G contains a vertex of degree at least k
| |
Dense graphs with a chromatic number k are more likely to have at least k(k-1)/2 edges
Question 48 |
60 | |
Question 49 |
color(vi) ← min{j ε N : no neighbour of vi is colored j}
Which of the following statements is/are TRUE?
This procedure results in a proper vertex coloring of G. | |
The number of colors used is at most Δ(G) + 1. | |
The number of colors used is at most Δ(G). | |
The number of colors used is equal to the chromatic number of G. |
Question 50 |
In a connected graph, a bridge is an edge whose removal disconnects a graph. Which one of the following statements is true?
A tree has no bridges | |
A bridge cannot be part of a simple cycle | |
Every edge of a clique with size 3 is a bridge (A clique is any complete sub graph of a graph) | |
A graph with bridges cannot have a cycle |
∴ (A) is false
Since, every edge in a complete graph kn(n≥3) is not a bridge ⇒
(C) is false
Let us consider the following graph G:
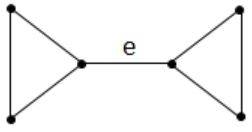
This graph has a bridge i.e., edge ‘e’ and a cycle of length ‘3’
∴ (D) is false
Since, in a cycle every edge is not a bridge
∴ (B) is true
Question 51 |
A graph is self-complementary if it is isomorphic to its complement for all self-complementary graphs on n vertices, n is
A multiple of 4 | |
Even | |
Odd | |
Congruent to 0 mod 4, or, 1 mod 4
|
Question 52 |
Let G be a connected planar graph with 10 vertices. If the number of edges on each face is three, then the number of edges in G is _______________.
24 | |
25 | |
26 | |
27 |
|V| + |R| = |E| + 2 ------(1) where |V|, |E|, |R| are respectively number of vertices, edges and faces (regions)
Given |V| = 10 ------(2) and number of edges on each face is three
∴3|R| = 2|E| ⇒ |R| = 2/3|E| ------(3)
Substituting (2), (3) in (1), we get
10 + 2/3|E| = |E| + 2 ⇒ |E|/3 = 8 ⇒ |E| = 24
Question 53 |
The minimum number of colours that is sufficient to vertex-colour any planar graph is ________.
4 | |
5 | |
6 | |
7 |
Here it is asked about the sufficient number of colors, so with the worst case of 4 colors we can color any planar graph.
Question 54 |
Let G be an undirected complete graph on n vertices, where n > 2. Then, the number of different Hamiltonian cycles in G is equal to
n! | |
1 | |
(n-1)! | |
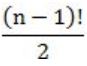 |
The total number of hamiltonian cycles in a complete graph are
(n-1)!/2, where n is number of vertices.
Question 55 |
Let G = (V,E) be a graph. Define ξ(G) = Σd id x d, where id is the number of vertices of degree d in G. If S and T are two different trees with ξ(S) = ξ(T),then
|S| = 2|T| | |
|S| = |T| - 1 | |
|S| = |T| | |
|S| = |T| + 1 |
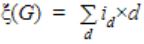
id= no. of vertices of degree ‘d’ in ‘G’
Eg:
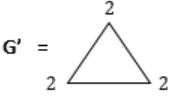
No. of vertices with degree ‘2’ = 3
ξ(G') = 3 × 2 = '6' i.e., sum of degrees
By Handshaking Theorem,
The sum of degrees would be equal to twice the no. of edges
|V| = 2|E|
It is given that ξ(G) = ξ(S) then
Sum of degrees of vertices in G is equal to sum of degrees of vertices in S
i.e., 2*(no. of edges in G) = 2*no. of edges in S no. of edges in G = no. of edges in S
Eg:
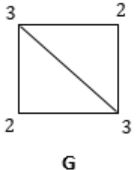
ξ(G) = (2 × 2) + (2 × 3) = 4 + 6 = 10
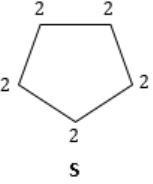
ξ(S) = 2 × 5 = 10
You can observe that, though no. of vertices are different, but still no. of edges are same.
Question 56 |
The degree sequence of a simple graph is the sequence of the degrees of the nodes in the graph in decreasing order. Which of the following sequences can not be the degree sequence of any graph?
- (I) 7, 6, 5, 4, 4, 3, 2, 1
(II) 6, 6, 6, 6, 3, 3, 2, 2
(III) 7, 6, 6, 4, 4, 3, 2, 2
(IV) 8, 7, 7, 6, 4, 2, 1, 1
I and II | |
III and IV | |
IV only | |
II and IV |
⇾ Arrange the degree of vertices in descending order
eg. d1, d2, d3... dn
⇾ Discard d1, subtrack ‘1’ from the next 'd1' degrees
eg:

⇒ 1 1 0 1
⇾ We should not get any negative value if its negative, this is not valid sequence
⇾ Repeat it till we get ‘0’ sequence
I. 7, 6, 5, 4, 4, 3, 2, 1
➡️5, 4, 3, 3, 2, 1, 0
➡️3, 2, 2, 1, 0, 0
➡️1, 1, 0, 0, 0
➡️0, 0, 0, 0
[valid]
II. 6, 6, 6, 6, 3, 3, 2, 2
➡️5, 5, 5, 2, 2, 1, 2
put them in descending order
➡️5, 5, 5, 2, 2, 2, 1
➡️4, 4, 1, 1, 1, 1
➡️3, 0, 0, 0, 1 (descending order)
➡️3, 1, 0, 0, 0
➡️0, -1, -1, 0
[This is not valid]
III. 7, 6, 6, 4, 4, 3, 2, 2
➡️5, 5, 3, 3, 2, 1, 1
➡️4, 2, 2, 1, 0, 1
➡️4, 2, 2, 1, 1, 0 (descending order)
➡️1, 1, 0, 0, 0
➡️0, 0, 0, 0
[valid]
IV. 8, 7, 7, 6, 4, 2, 1, 1
There is a degree ‘8’, but there are only ‘8’ vertices.
A vertex cannot have edge to itself in a simple graph. This is not valid sequence.
Question 57 |
Let G be the non-planar graph with the minimum possible number of edges. Then G has
9 edges and 5 vertices | |
9 edges and 6 vertices | |
10 edges and 5 vertices | |
10 edges and 6 vertices |
if n ≥ 3 then e ≤ 3n-6 (for planarity)
where n = no. of vertices
e = no. of edges
Now lets check the options.
A) e=9, n=5
9 ≤ 3(5) - 6
9 ≤ 15 - 6
9 ≤ 9
Yes, it is planar.
B) e=9, n=6
9 ≤ 3(6) - 6
9 ≤ 18 - 6 9 ≤ 12 Yes, it is planar.
iii) e=10, n=5
10 ≤ 3(5) - 6
10 ≤ 15 - 6
10 ≤ 9 No, it is not planar.
So, option C is non-planar graph.
iv) e=10, n=6
10 ≤ 3(6) - 6
10 ≤ 18 - 6
10 ≤ 12
Yes, it is planar.
Question 58 |
Which of the following graphs has an Eulerian circuit?
Any k-regular graph where k is an even number. | |
A complete graph on 90 vertices. | |
The complement of a cycle on 25 vertices.
| |
None of the above. |
→ all vertices in the graph have an "even degree".
→ And the graph must be corrected.
Now in option (C) it is saying that the complement of a cycle on 25 vertices without complement the degree of each vertex is 2.
Now since there are 25 vertices, so maximum degree of each vertex will be 24 and so in complement of cycle each vertex degree will be 24 - 2 = 22.
There is a theorem which says "G be a graph with n vertices and if every vertex has a degree of atleast n-1/2 then G is connected."
So we can say that complement of cycle with 25 vertices fulfills both the conditions, and hence is Eulerian circuit.
Question 59 |
What is the chromatic number of an n-vertex simple connected graph which does not contain any odd length cycle? Assume n ≥ 2.
2 | |
3 | |
n-1 | |
n |
Eg: Consider a square, which has 4 edges. It can be represented as bipartite ,with chromatic number 2.
Question 60 |
Which one of the following is TRUE for any simple connected undirected graph with more than 2 vertices?
No two vertices have the same degree. | |
At least two vertices have the same degree. | |
At least three vertices have the same degree. | |
All vertices have the same degree.
|
If all vertices have different degrees, then the degree sequence will be {1,2,3,....n-1}, it will not have ‘n’( A simple graph will not have edge to itself, so it can have edges with all other (n-1) vertices). Degree sequence has only (n-1) numbers, but we have ‘n’ vertices. So, by Pigeonhole principle there are two vertices which has same degree.
Method 2:
A) Consider a triangle, all vertices has same degree, so it is false
C) Consider a square with one diagonal, there are less than three vertices with same degree, so it is false
D) Consider a square with one diagonal, vertices have different degrees. So, it is false.
We can conclude that option B is correct.
Question 61 |
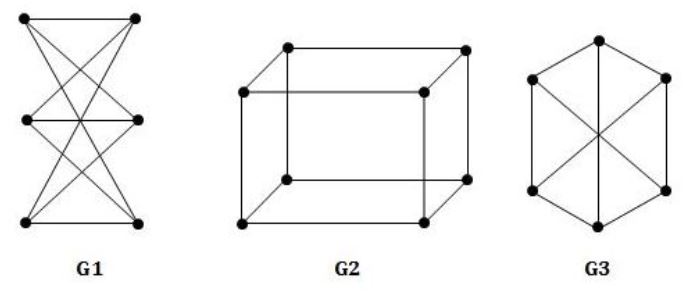
K4 and Q3 are graphs with the following structures.
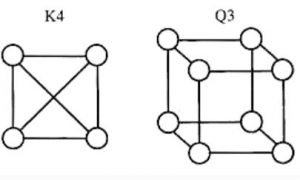
Which one of the following statement is TRUE in relation to these graphs?
K4 is planar while Q3 is not | |
Both K4 and Q3 are planar | |
Q3 is planar while K4 is not | |
Neither K4 not Q3 is planar |
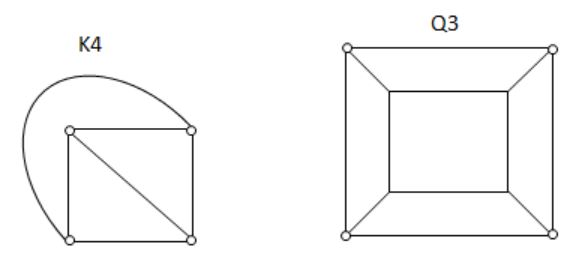
Both the above graphs are planar.
Question 62 |
Let G be a simple undirected planar graph on 10 vertices with 15 edges. If G is a connected graph, then the number of bounded faces in any embedding of G on the plane is equal to
3 | |
4 | |
5 | |
6 |
v-e+f = 2
Given 10 vertices & 15 edges
10-15+f = 2
f = 2+15-10
f = 7
There will be an unbounded face always. So, number of faces = 6.
