Linked-List
Question 1 |
#include<stdio.h>
#include<stdlib.h>
Struct Node{
int value;
struct Node *next;};
int main() {
struct Node *boxE, *head, *boxN; int index = 0;
boxE = head = (struct Node *) malloc(sizeof(struct Node));
head->value = index;
for (index = 1; index <= 3; index++) {
boxN = (struct Node *) malloc(sizeof(struct Node));
boxE->next = boxN;
boxN->value = index;
boxE = boxN; }
for (index = 0; index <= 3; index++) {
printf(“Value at index %d is %d\n”, index, head->value);
head = head->next;
printf(“Value at index %d is %d\n”, index+1, head->value); } }
Which one of the statements below is correct about the program?
Upon execution, the program creates a linked-list of five nodes. | |
It dereferences an uninitialized pointer that may result in a run-time error. | |
Upon execution, the program goes into an infinite loop. | |
It has a missing return which will be reported as an error by the compiler. |
One node is created with value 0.
Loop i runs from 1 to 3. Hence total 4 nodes will be created.
0 → 1 → 2 → 3 → NULL
When index =3, head =3
Head = Head → Next
Head → Value from printf will generate an error.
Question 2 |
What is the worst case time complexity of inserting n elements into an empty linked list, if the linked list needs to be maintained in sorted order?
θ(n log n) | |
θ(n2) | |
θ(1) | |
θ(n) |
Total number of elements inserted into an empty linked list is O(n). So, it will take O(n) time in the worst case.
After inserting elements into an empty linked list we have to perform sorting operation.
To get minimum time complexity to perform sorting order is merge sort. It will give O(nlogn) time complexity only.
Let head be the first node of the linked list to be sorted and head Reference be the pointer to head.
The head in MergeSort as the below implementation changes next links to sort the linked lists (not data at the nodes), so head node has to be changed if the data at the original head is not the smallest value in the linked list.
Note: There are other sorting methods also will give decent time complexity but quicksort will give O(n2) and heap sort will not be suitable to apply.
Question 3 |
The concatenation of two lists is to be performed in O(1) time. Which of the following implementations of a list should be used?
Singly linked list | |
Doubly linked list | |
Circular doubly linked list | |
Array implementation of list |
Question 4 |
Let p be a pointer as shown in the figure in a single linked list.

What do the following assignment statements achieve?
- q: = p → next
p → next:= q → next
q → next:=(q → next) → next
(p → next) → next:= q
(b) Compute the postfix equivalent of the following Infix expression
3 * log(x+1) - a/2
Theory Explanation. |
Question 5 |
log n | |
n/2 | |
(log2)n - 1 | |
n |
Question 6 |
Consider the function f defined below.
struct item {
int data;
struct item * next;
};
int f(struct item *p) {
return ((p == NULL) || (p->next == NULL) ||
((P->data <= p->next->data) &&
f(p->next)));
}
For a given linked list p, the function f returns 1 if and only if
the list is empty or has exactly one element | |
the elements in the list are sorted in non-decreasing order of data value
| |
the elements in the list are sorted in non-increasing order of data value
| |
not all elements in the list have the same data value |
Question 7 |
A circularly linked list is used to represent a Queue. A single variable p is used to access the Queue. To which node should p point such that both the operations enQueue and deQueue can be performed in constant time?
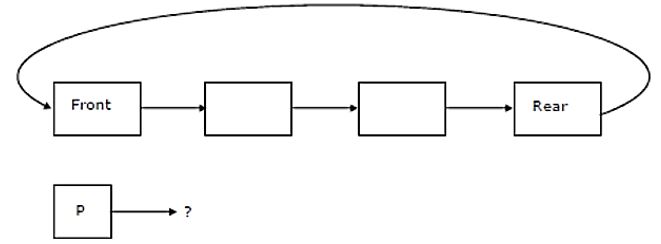
rear node | |
front node | |
not possible with a single pointer | |
node next to front |
Question 8 |
Suppose each set is represented as a linked list with elements in arbitrary order. Which of the operations among union, intersection, membership, cardinality will be the slowest?
union only | |
intersection, membership
| |
membership, cardinality | |
union, intersection |
Let no. of elements in list 2 be n2.
Union:
To union two lists, for each element in one list we will search in other list, to avoid duplicates. So, time complexity will be O(n1×n2).
Intersection:
To take intersection of two lists, for each element in one list we will search in other list if it is present or not. So time complexity will be O(n1 × n2).
Membership:
In this we search if particular element is present in the list or not. So time complexity will be O(n1 + n2).
Cardinality:
In this we find the size of set or list. So to find size of list we have to traverse each list once. So time complexity will be O(n1+n2).
Hence, Union and Intersection will be slowest.
Question 9 |
Linked lists are not suitable data structures of which one of the following problems?
Insertion sort | |
Binary search | |
Radix sort | |
Polynomial manipulation
|
Question 10 |
Consider a singly linked list having n nodes. The data items d1, d2, ...dn are stored in these n nodes. Let X be a pointer to the j-th node (1≤j≤n) in which dj is stored. A new data item d stored in node with address Y is t be inserted. Give an algorithm to insert d into the list to obtain a list having items d1, d2, ..., dj-1, dj, ..., dn in the order without using the header.
Theory Explanation. |
Question 11 |
Suggest a data structure for representing a subnet S of integers from 1 to n. Following operations on the set S are to be performed in constant time (independent of cardinality of S).
(i) MEMBER(X): Check whether X is the set S or not
(ii) FIND-ONE(S): If S is not empty, return one element of the set S
(any arbitrary element will do)
(iii) ADD(X): Add integer x to set S
(iv) DELETE(X): Delete integer x from S.
Give pictorial examples of your data structure. Give routines for these operations in an English like language. You may assume that the data structure has been suitably initialized. Clearly state your assumptions regarding initialization.
Theory Explanation. |
Question 12 |
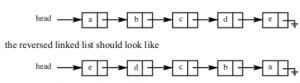 Which one of the following statements is TRUE about the time complexity of algorithms that solve the above problem in O (1) space?
Which one of the following statements is TRUE about the time complexity of algorithms that solve the above problem in O (1) space?
 | |
 | |
 | |
It is not possible to reverse a singly linked list in O (1) space. |
struct Node {
int data;
struct Node* next;
{
this->data = data;
next = NULL;
}
};
struct LinkedList {
Node* head;
LinkedList() { head = NULL; }
/* Function to reverse the linked list */
void reverse()
{
// Initialize current, previous and
// next pointers
Node* current = head;
Node *prev = NULL, *next = NULL;
while (current != NULL) {
// Store next
next = current->next;
// Reverse current node's pointer
current->next = prev;
// Move pointers one position ahead.
prev = current;
current = next;
}
head = prev;
}
For the above algorithm :
Time Complexity: O(n)
Space Complexity: O(1)
Question 13 |
Let P be a singly linked list. Let Q be the pointer to an intermediate node x in the list. What is the worst-case time complexity of the best known algorithm to delete the node x from the list?
O(n) | |
O(log2 n) | |
O(logn) | |
O(1) |
