Multiplexer
Question 1 |
Consider the circuit in below figure. f implements
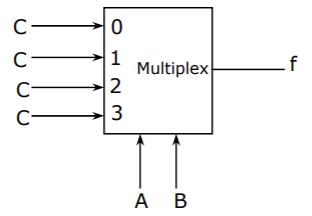
 | |
A + B + C | |
A ⊕ B ⊕ C | |
AB + BC + CA |
Question 1 Explanation:
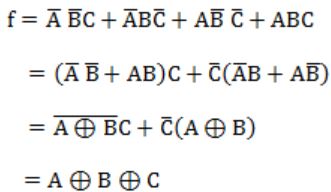
Question 2 |
A logic network has two data inputs A and B, and two control inputs C0 and C1. It implements the function F according to the following table.

Implement the circuit using one 4 to 1 Multiplexer, one 2-input Exclusive OR gate, one 2-input AND gate, one 2-input OR gate and one Inverter.
Theory Explanation. |
Question 3 |
A multiplexor with a 4 bit data select input is a
4:1 multiplexor | |
2:1 multiplexor | |
16:1 multiplexor | |
8:1 multiplexor |
Question 3 Explanation:
For 'n' bit data it selects 2n : 1 input
For 4 bit data it selects 24 : 1 = 16: 1 input
For 4 bit data it selects 24 : 1 = 16: 1 input
Question 4 |
The maximum gate delay for any output to appear in an array multiplier for multiplying two n bit number is
On2 | |
O(n) | |
O(log n) | |
O(1) |
Question 4 Explanation:
Total no. of gates being used for 'n' bit multiplication in an array multiplier (n*n) = (2n-1)
Total delay = 1 * 2n - 1 = O(2n - 1) = n
Total delay = 1 * 2n - 1 = O(2n - 1) = n
There are 4 questions to complete.
