Queues-and-Stacks
Question 1 |
Let Q denote a queue containing sixteen numbers and S be an empty stack. Head(Q) returns the element at the head of the queue Q without removing it from Q. Similarly Top(S) returns the element at the top of S without removing it from S. Consider the algorithm given below.
The maximum possible number of iterations of the while loop in the algorithm is _________.
256 | |
257 | |
258 | |
259 |
Question 1 Explanation:
The maximum possible number of iterations of the while loop in this algorithm is:
Try to solve it for 3 numbers [1. 2, 3].
Step 1: Initially Queue contains 3 elements so after 5 while loop iterations queue contains 3, 2 and stack contains 1.
Step 2: Now after 3 more while loop iterations, Queue contains 3 and stack contains 1, 2 (TOS = 2).
Step 3: After 1 more while loop iteration, push 3 onto the stack so queue is empty and stack contains 1, 2, 3 {top = 3}.
So, total number of iterations will be 5 + 3 + 1 = 9
i.e., for 3 it is 9 iterations (3*3)
for 4 it is 16 iterations (4*4)
Given: 16 numbers, so 16 * 16 = 256
Try to solve it for 3 numbers [1. 2, 3].
Step 1: Initially Queue contains 3 elements so after 5 while loop iterations queue contains 3, 2 and stack contains 1.
Step 2: Now after 3 more while loop iterations, Queue contains 3 and stack contains 1, 2 (TOS = 2).
Step 3: After 1 more while loop iteration, push 3 onto the stack so queue is empty and stack contains 1, 2, 3 {top = 3}.
So, total number of iterations will be 5 + 3 + 1 = 9
i.e., for 3 it is 9 iterations (3*3)
for 4 it is 16 iterations (4*4)
Given: 16 numbers, so 16 * 16 = 256
Question 2 |
A queue Q containing n items and an empty stack S are given. It is required to transfer all the items from the queue to the stack, so that the item at the front of queue is on the top of the stack, and the order of all other items is preserved. Show how this can be done in O(n) time using only a constant amount of additional storage. Note that the only operations which can be performed on the queue and stack are Delete, Insert, Push and Pop. Do not assume any implementation of the queue or stack.
Theory Explanation. |
Question 3 |
A stack is used to pass parameters to procedures in a procedure call.
(a) If a procedure P has two parameters as described in procedure definition:
procedure P (var x :integer; y: integer);
and if P is called by ; P(a,b)
State precisely in a sentence what is pushed on stack for parameters a and b.
(b) In the generated code for the body of procedure P, how will the addressing of formal parameters x and y differ?
Theory Explanation. |
Question 4 |
A function f defined on stacks of integers satisfies the following properties.
f(∅) = 0 and f (push (S, i)) = max (f(S), 0) + i for all stacks S and integers i.
If a stack S contains the integers 2, -3, 2, -1, 2 in order from bottom to top, what is f(S)?
6 | |
4 | |
3 | |
2 |
Question 4 Explanation:
2, -3, 2, -1, 2
f(Ø)=0 and f(push(S,i) = max(f(S),0) + i;
Initially stack is empty and for empty stack 0 is given.
f(push(0,2)) = max(f(Ø),0) + 2 = max(Ø,0) + 2 = 2
f(push(2,-3)) = max(2,0) + (-3) = 2 - 3 = -1
f(push(-1,2)) = max(-1,0) + 2 = 0 + 2 = 2
f(push(2,-1)) = max(2,0)+ (-1) = 2 - 1 = 1
f(push(1,2)) = max(1,0) + 2 = 1 + 2 = 3
So, 3 will be the answer.
∴ Option C is correct.
f(Ø)=0 and f(push(S,i) = max(f(S),0) + i;
Initially stack is empty and for empty stack 0 is given.
f(push(0,2)) = max(f(Ø),0) + 2 = max(Ø,0) + 2 = 2
f(push(2,-3)) = max(2,0) + (-3) = 2 - 3 = -1
f(push(-1,2)) = max(-1,0) + 2 = 0 + 2 = 2
f(push(2,-1)) = max(2,0)+ (-1) = 2 - 1 = 1
f(push(1,2)) = max(1,0) + 2 = 1 + 2 = 3
So, 3 will be the answer.
∴ Option C is correct.
Question 5 |
Consider the following sequence of operations on an empty stack.
push(54); push(52); pop(); push(55); push(62); s=pop();
Consider the following sequence of operations on an empty queue.
enqueue(21); enqueue(24); dequeue(); enqueue(28); enqueue(32); q = dequeue();
The value of s + q is ________
push(54); push(52); pop(); push(55); push(62); s=pop();
Consider the following sequence of operations on an empty queue.
enqueue(21); enqueue(24); dequeue(); enqueue(28); enqueue(32); q = dequeue();
The value of s + q is ________
86 |
Question 5 Explanation:
push(54) ⇒ 54
push(52)=> 54, 52(top)
pop() ⇒ 54 (top)
push(55)==> 54, 55(top)
push(62) ⇒ 54,55,62(top)
s=pop() ⇒ 62 will store into the variable s then s=62
enqueue(21) ⇒ (front) 21(rear)
enqueue(24) ⇒ (Front)21, 24(rear)
dequeue()==> (front) 24(rear)
enqueue(28) ===> (front) 24,28 (rear)
enqueue(32)====>(front) 24,28,32 (rear)
q=dequeue() ⇒ value 24 will store into the variable “q”
q=24
S+q =62+24 =86
Question 6 |
Consider a sequence a of elements a0 = 1, a1 = 5, a2 = 7, a3 = 8, a4 = 9, and a5 = 2. The following operations are performed on a stack S and a queue Q, both of which are initially empty.
I: push the elements of a from a0 to a5 in that order into S.
II: enqueue the elements of a from a0 to a5 in that order into Q.
III: pop an element from S.
IV: dequeue an element from Q.
V: pop an element from S.
VI: dequeue an element from Q.
VII: dequeue an element from Q and push the same element into S.
VIII: Repeat operation
VII three times. IX: pop an element from S. X: pop an element from S.
The top element of S after executing the above operations is _____?
I: push the elements of a from a0 to a5 in that order into S.
II: enqueue the elements of a from a0 to a5 in that order into Q.
III: pop an element from S.
IV: dequeue an element from Q.
V: pop an element from S.
VI: dequeue an element from Q.
VII: dequeue an element from Q and push the same element into S.
VIII: Repeat operation
VII three times. IX: pop an element from S. X: pop an element from S.
The top element of S after executing the above operations is _____?
8 |
Question 6 Explanation:
Given the sequence “a” of elements a0 = 1, a1 = 5, a2 = 7, a3 = 8, a4 = 9, and a5 = 2.
I: push the elements from a0 to a5 in that order into S.
II: enqueue the elements of a from a0 to a5 in that order into Q.
III: pop an element from S.
IV: dequeue an element from Q.
V: pop an element from S.
VI: dequeue an element from Q.
VII: dequeue an element from Q and push the same element into S.
Element “7” is deleted and inserted into stack “S”
VIII: Repeat operation VII three times.
After performing the VIII operation , the elements of stack are as shown below
IX: pop an element from S.
X: pop an element from S
The top element of S after executing the above operations is 8.
I: push the elements from a0 to a5 in that order into S.
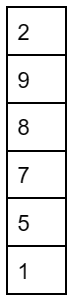
II: enqueue the elements of a from a0 to a5 in that order into Q.
III: pop an element from S.
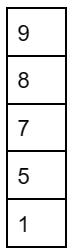
IV: dequeue an element from Q.
V: pop an element from S.
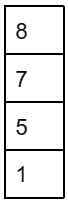
VI: dequeue an element from Q.
VII: dequeue an element from Q and push the same element into S.
Element “7” is deleted and inserted into stack “S”
VIII: Repeat operation VII three times.
After performing the VIII operation , the elements of stack are as shown below
IX: pop an element from S.
X: pop an element from S
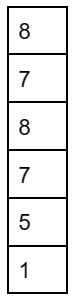
The top element of S after executing the above operations is 8.
Question 7 |
The five items: A, B, C, D, and E are pushed in a stack, one after other starting from A. The stack is popped four items and each element is inserted in a queue. The two elements are deleted from the queue and pushed back on the stack. Now one item is popped from the stack. The popped item is
A | |
B | |
C | |
D |
Question 7 Explanation:
When five items: A, B, C, D, and E are pushed in a stack: Order of stack becomes: A, B, C, D, and E (A at the bottom and E at the top.) stack is popped four items and each element is inserted in a queue: Order of queue: B, C, D, E (B at rear and E at the front) Order of stack after pop operations = A. Two elements deleted from the queue and pushed back stack: New order of stack = A, E, D(A at the bottom, D at the top) As D is on the top so when pop operation occurs D will be popped out. So, correct option is (D).
Question 8 |
The best data structure to check whether an arithmetic expression has balanced parenthesis is a
Queue | |
Stack | |
Tree | |
List |
Question 8 Explanation:
→ The stack is the best data structure to validate the arithmetic expression.
→ While evaluating when left parentheses occur then it pushes into the stack when right parentheses occur pop from the stack. While at the end there is empty in the stack.
→ While evaluating when left parentheses occur then it pushes into the stack when right parentheses occur pop from the stack. While at the end there is empty in the stack.
Question 9 |
The following postfix expression with single digit operands is evaluated using a stack:
8 2 3 ^ / 2 3 * + 5 1 * –
Note that ^ is the exponentiation operator. The top two elements of the stack after the first * is evaluated are
8 2 3 ^ / 2 3 * + 5 1 * –
Note that ^ is the exponentiation operator. The top two elements of the stack after the first * is evaluated are
6,1 | |
5,7 | |
3,2 | |
1,5 |
Question 9 Explanation:
Expression: 8 2 3 ^ / 2 3 * + 5 1 * –
Rule (1): If the element is a number, Push it into stack.
Rule (2): If the element is an operator, Pop operands from the stack. Evaluate the operator operation and Push the result back into the stack.
Rule (1): If the element is a number, Push it into stack.
Rule (2): If the element is an operator, Pop operands from the stack. Evaluate the operator operation and Push the result back into the stack.
Question 10 |
The five items: A, B, C, D, and E are pushed in a stack, one after other starting from A. The stack is popped four items and each element is inserted in a queue. The two elements are deleted from the queue and pushed back on the stack. Now one item is popped from the stack. The popped item is
A | |
B | |
C | |
D |
Question 10 Explanation:
Question 11 |
Consider a standard Circular Queue ‘q’ implementation (which has the same condition for Queue Full and Queue Empty) whose size is 11 and the elements of the queue are q[0], q[1], q[2]…..,q[10].
The front and rear pointers are initialized to point at q[2] . In which position will the ninth element be added?
q[0] | |
q[1] | |
q[9] | |
q[10] |
Question 11 Explanation:
A circular queue is a data structure that uses a single, fixed-size buffer as if it were connected end-to-end.
The front and rear pointers are initialized to point at q[2] which means third element.
First element will add at q[3] , second element will add at q[4] and so on eight element will add at q[10].
Q[10] is the end of the queue which is connected to q[0]
So ninth element can be added at q[0] pointer
The front and rear pointers are initialized to point at q[2] which means third element.
First element will add at q[3] , second element will add at q[4] and so on eight element will add at q[10].
Q[10] is the end of the queue which is connected to q[0]
So ninth element can be added at q[0] pointer
Question 12 |
The five items: A, B, C, D, and E are pushed in a stack, one after other starting from A. The stack is popped four items and each element is inserted in a queue. The two elements are deleted from the queue and pushed back on the stack. Now one item is popped from the stack. The popped item is
A | |
B | |
C | |
D |
Question 12 Explanation:
Stack representation after inserting 5 elements
Question 13 |
Which of the following is NOT represented in a subroutine activation record frame for a stack-based programming language?
Values of local variables | |
Return address | |
Heap area | |
Information needed to access non local variables |
Question 13 Explanation:
Stack is used for static memory allocation and Heap for dynamic memory allocation, both stored in the computer's RAM .
Variables allocated on the stack are stored directly to the memory and access to this memory is very fast, and it's allocation is dealt with when the program is compiled
Variables allocated on the heap have their memory allocated at run time and accessing this memory is a bit slower, but the heap size is only limited by the size of virtual memory . Element of the heap have no dependencies with each other and can always be accessed randomly at any time
Variables allocated on the stack are stored directly to the memory and access to this memory is very fast, and it's allocation is dealt with when the program is compiled
Variables allocated on the heap have their memory allocated at run time and accessing this memory is a bit slower, but the heap size is only limited by the size of virtual memory . Element of the heap have no dependencies with each other and can always be accessed randomly at any time
Question 14 |
A__ is a linear list in which insertions and deletions are made to from either end of the structure.
Circular queue | |
Priority queue | |
Stack | |
Dequeue |
Question 14 Explanation:
● A deque, also known as a double ended queue, is an ordered collection of items similar to the queue. It has two ends, a front and a rear, and the items remain positioned in the collection.
● What makes a deque different is the unrestrictive nature of adding and removing items.New items can be added at either the front or the rear.
● Likewise, existing items can be removed from either end. In a sense, this hybrid linear structure provides all the capabilities of stacks and queues in a single data structure.
● What makes a deque different is the unrestrictive nature of adding and removing items.New items can be added at either the front or the rear.
● Likewise, existing items can be removed from either end. In a sense, this hybrid linear structure provides all the capabilities of stacks and queues in a single data structure.
Question 15 |
Following is C like Pseudo code of a function that takes a number as an argument, and uses a stack S to do argument, and uses a stack S to do processing.
void fun(int n)
{
Stack s;//Say it creates an empty stack S
while(n>0)
{
// This line pushes the value of n%2 to
Stack S;
Push(&S,n%2);
n=n/2l
}
// Run while Stack S is not empty
while(!is Empty(&S)) Printf(%d",pop(&S));//pop an element from S and print it
}
What does the above function do in general order
void fun(int n)
{
Stack s;//Say it creates an empty stack S
while(n>0)
{
// This line pushes the value of n%2 to
Stack S;
Push(&S,n%2);
n=n/2l
}
// Run while Stack S is not empty
while(!is Empty(&S)) Printf(%d",pop(&S));//pop an element from S and print it
}
What does the above function do in general order
Prints binary representation of n in reverse order | |
prints binary representation of n | |
Prints the value of Logn | |
Prints the value of Logn in reverse order |
Question 15 Explanation:
For any number, we can check whether its ‘i’th bit is 0(OFF) or 1(ON) by bitwise ANDing it with “2^i” (2 raise to i).,
1) Let us take number 'NUM' and we want to check whether it's 0th bit is ON or OFF
bit = 2 ^ 0 (0th bit)
if NUM & bit == 1 means 0th bit is ON else 0th bit is OFF
2) Similarly if we want to check whether 5th bit is ON or OFF
bit = 2 ^ 5 (5th bit)
if NUM & bit == 1 means its 5th bit is ON else 5th bit is OFF.
Let us take unsigned integer (32 bit), which consist of 0-31 bits. To print binary representation of unsigned integer, start from 31th bit, check whether 31th bit is ON or OFF, if it is ON print “1” else print “0”. Now check whether 30th bit is ON or OFF, if it is ON print “1” else print “0”, do this for all bits from 31 to 0, finally we will get binary representation of number. void bin(unsigned n)
{
unsigned i;
for (i = 1 << 31; i > 0; i = i / 2)
(n & i)? printf("1"): printf("0");
}
int main(void)
{
bin(7);
printf("\n");
bin(4);
}
1) Let us take number 'NUM' and we want to check whether it's 0th bit is ON or OFF
bit = 2 ^ 0 (0th bit)
if NUM & bit == 1 means 0th bit is ON else 0th bit is OFF
2) Similarly if we want to check whether 5th bit is ON or OFF
bit = 2 ^ 5 (5th bit)
if NUM & bit == 1 means its 5th bit is ON else 5th bit is OFF.
Let us take unsigned integer (32 bit), which consist of 0-31 bits. To print binary representation of unsigned integer, start from 31th bit, check whether 31th bit is ON or OFF, if it is ON print “1” else print “0”. Now check whether 30th bit is ON or OFF, if it is ON print “1” else print “0”, do this for all bits from 31 to 0, finally we will get binary representation of number. void bin(unsigned n)
{
unsigned i;
for (i = 1 << 31; i > 0; i = i / 2)
(n & i)? printf("1"): printf("0");
}
int main(void)
{
bin(7);
printf("\n");
bin(4);
}
Question 16 |
Assume that the operators +,-,x are left associative and 6 right associative. the order of precedence(from highest to lowest) is 6,x,+,-. The postfix expression corresponding to the infix expression
a+bxc-d^e^f is
abc x+def^^- | |
abc xde^f^- | |
ab +c xd -e^f ^ | |
-+ a x bc ^^def |
Question 16 Explanation:
a+bc-d＾e＾f
⟶ left to right
Step 1: abc+
⟶ left to right
Step 1: abc+
Question 17 |
A priority queue is implemented as a Max-heap. Initially, it has 5 elements. The level-order traversal of the heap is: 10,8,5,3,2. Two new elements 1 and 7 are inserted into the heap in that order. The level-order traversal of the heap after the insertion of the elements is
10,8,7,3,2,1,5 | |
10,8,7,2,3,1,5 | |
10,8,7,1,2,3,5 | |
10,8,7,5,3,2,1 |
Question 17 Explanation:
Max-Heap has 5 elements:
The level order traversal in this max heap final is:
10, 8, 7, 3, 2, 1, 5.
The level order traversal in this max heap final is:10, 8, 7, 3, 2, 1, 5.
Question 18 |
A queue is implemented using an array such that ENQUEUE and DEQUEUE operations are performed efficiently. Which one of the following statements is CORRECT(n refers to the number of items in the QUEUE)?
Both operations can be performed in O(1) time |
Question 18 Explanation:
Since it is mentioned in the question that both of the operations are performed efficiently. Hence even the worst case time complexity will be O(1) by the use of the Circular queue there won't be any need of shifting in the array.
Question 19 |
How many PUSH and POP operations will be needed to evaluate the following expression by reverse polish notation in a stack machine (A * B) + (C * D/E) ?
4 PUSH and 3 POP instructions | |
5 PUSH and 4 POP instructions | |
6 PUSH and 2 POP instructions | |
5 PUSH and 3 POP instructions |
Question 19 Explanation:
Given infix notation, we have to change infix notation into postfix notation.
after converting postfix notation the notations are ab* cde /* +
Total 5 PUSH and 4 POP operations performed.
after converting postfix notation the notations are ab* cde /* +
Total 5 PUSH and 4 POP operations performed.
Question 20 |
Which of the following permutation can be obtained in the same order using a stack assuming that input is the sequence 5, 6, 7, 8, 9 in that order?
7, 8, 9, 5, 6 | |
5, 9, 6, 7, 8 | |
7, 8, 9, 6, 5 | |
9, 8, 7, 5, 6 |
Question 20 Explanation:
Push 5 Push 6 Push 7 Pop 7 Push 8 Pop 8 Push 9 Pop 9 Pop 6 Pop 5.
→ Remaining options are not possible.
→ Remaining options are not possible.
Question 21 |
The minimum number of stacks needed to implement a queue is
3 | |
1 | |
2 | |
4 |
Question 21 Explanation:
Minimum number of stacks of size n required to implement a queue of size n is two. With the help of two stacks we can able to implement a queue.
Question 22 |
If the sequence of operations – push (1), push (2), pop, push (1), push (2), pop, pop, pop, push (2), pop are performed on a stack, the sequence of popped out values
2,2,1,1,2 | |
2,2,1,2,2 | |
2,1,2,2,1 | |
2,1,2,2,2
|
Question 22 Explanation:
Final Pop sequence: 22112
There are 22 questions to complete.