Queues-and-Stacks
Question 1 |
Consider the following statements:
- (i) First-in-first out types of computations are efficiently supported by STACKS.
(ii) Implementing LISTS on linked lists is more efficient than implementing LISTS on an array for almost all the basic LIST operations.
(iii) Implementing QUEUES on a circular array is more efficient than implementing QUEUES on a linear array with two indices.
(iv) Last-in-first-out type of computations are efficiently supported by QUEUES.
Which of the following is correct?
(ii) and (iii) are true | |
(i) and (ii) are true | |
(iii) and (iv) are true | |
(ii) and (iv) are true |
(iv) LIFO computation efficiently supported by stacks.
Then given (i) and (iv) are false.
Answer:- A
Question 2 |
A priority queue Q is used to implement a stack that stores characters. PUSH (C) is implemented INSERT (Q, C, K) where K is an appropriate integer key chosen by the implementation. POP is implemented as DELETEMIN(Q). For a sequence of operations, the keys chosen are in
non-increasing order | |
non-decreasing order | |
strictly increasing order | |
strictly decreasing order |
Question 3 |
What is the minimum number of stacks of size n required to implement a queue of size n?
One | |
Two | |
Three | |
Four |
Question 4 |
A queue Q containing n items and an empty stack S are given. It is required to transfer all the items from the queue to the stack, so that the item at the front of queue is on the top of the stack, and the order of all other items is preserved. Show how this can be done in O(n) time using only a constant amount of additional storage. Note that the only operations which can be performed on the queue and stack are Delete, Insert, Push and Pop. Do not assume any implementation of the queue or stack.
Theory Explanation. |
Question 5 |
A stack is used to pass parameters to procedures in a procedure call.
(a) If a procedure P has two parameters as described in procedure definition:
procedure P (var x :integer; y: integer);
and if P is called by ; P(a,b)
State precisely in a sentence what is pushed on stack for parameters a and b.
(b) In the generated code for the body of procedure P, how will the addressing of formal parameters x and y differ?
Theory Explanation. |
Question 6 |
push(54); push(52); pop(); push(55); push(62); s=pop();
Consider the following sequence of operations on an empty queue.
enqueue(21); enqueue(24); dequeue(); enqueue(28); enqueue(32); q = dequeue();
The value of s + q is ________
86 |
push(54) ⇒ 54
push(52)=> 54, 52(top)
pop() ⇒ 54 (top)
push(55)==> 54, 55(top)
push(62) ⇒ 54,55,62(top)
s=pop() ⇒ 62 will store into the variable s then s=62
enqueue(21) ⇒ (front) 21(rear)
enqueue(24) ⇒ (Front)21, 24(rear)
dequeue()==> (front) 24(rear)
enqueue(28) ===> (front) 24,28 (rear)
enqueue(32)====>(front) 24,28,32 (rear)
q=dequeue() ⇒ value 24 will store into the variable “q”
q=24
S+q =62+24 =86
Question 7 |
A function f defined on stacks of integers satisfies the following properties.
f(∅) = 0 and f (push (S, i)) = max (f(S), 0) + i for all stacks S and integers i.
If a stack S contains the integers 2, -3, 2, -1, 2 in order from bottom to top, what is f(S)?
6 | |
4 | |
3 | |
2 |
f(Ø)=0 and f(push(S,i) = max(f(S),0) + i;
Initially stack is empty and for empty stack 0 is given.
f(push(0,2)) = max(f(Ø),0) + 2 = max(Ø,0) + 2 = 2
f(push(2,-3)) = max(2,0) + (-3) = 2 - 3 = -1
f(push(-1,2)) = max(-1,0) + 2 = 0 + 2 = 2
f(push(2,-1)) = max(2,0)+ (-1) = 2 - 1 = 1
f(push(1,2)) = max(1,0) + 2 = 1 + 2 = 3
So, 3 will be the answer.
∴ Option C is correct.
Question 8 |
I: push the elements of a from a0 to a5 in that order into S.
II: enqueue the elements of a from a0 to a5 in that order into Q.
III: pop an element from S.
IV: dequeue an element from Q.
V: pop an element from S.
VI: dequeue an element from Q.
VII: dequeue an element from Q and push the same element into S.
VIII: Repeat operation
VII three times. IX: pop an element from S. X: pop an element from S.
The top element of S after executing the above operations is _____?
8 |
I: push the elements from a0 to a5 in that order into S.
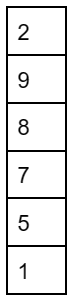
II: enqueue the elements of a from a0 to a5 in that order into Q.

III: pop an element from S.
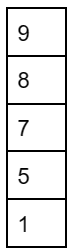
IV: dequeue an element from Q.

V: pop an element from S.
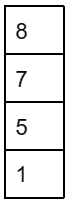
VI: dequeue an element from Q.

VII: dequeue an element from Q and push the same element into S.
Element “7” is deleted and inserted into stack “S”

VIII: Repeat operation VII three times.
After performing the VIII operation , the elements of stack are as shown below

IX: pop an element from S.

X: pop an element from S
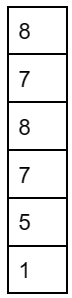
The top element of S after executing the above operations is 8.
Question 9 |
Let Q denote a queue containing sixteen numbers and S be an empty stack. Head(Q) returns the element at the head of the queue Q without removing it from Q. Similarly Top(S) returns the element at the top of S without removing it from S. Consider the algorithm given below.

The maximum possible number of iterations of the while loop in the algorithm is _________.
256 | |
257 | |
258 | |
259 |
Try to solve it for 3 numbers [1. 2, 3].
Step 1: Initially Queue contains 3 elements so after 5 while loop iterations queue contains 3, 2 and stack contains 1.
Step 2: Now after 3 more while loop iterations, Queue contains 3 and stack contains 1, 2 (TOS = 2).
Step 3: After 1 more while loop iteration, push 3 onto the stack so queue is empty and stack contains 1, 2, 3 {top = 3}.
So, total number of iterations will be 5 + 3 + 1 = 9
i.e., for 3 it is 9 iterations (3*3)
for 4 it is 16 iterations (4*4)
Given: 16 numbers, so 16 * 16 = 256
Question 10 |
An implementation of a queue Q, using two stacks S1 and S2, is given below:
void insert(Q, x) {
push (S1, x);
}
void delete(Q){
if(stack-empty(S2)) then
if(stack-empty(S1)) then {
print(“Q is empty”);
return;
}
else while (!(stack-empty(S1))){
x=pop(S1);
push(S2,x);
}
x=pop(S2);
}
Let n insert and m(<=n) delete operations be performed in an arbitrary order on an empty queue Q. Let x and y be the number of push and pop operations performed respectively in the process. Which one of the following is true for all m and n?
n+m ≤ x < 2n and 2m ≤ y ≤ n+m | |
n+m ≤ x< 2n and 2m ≤y ≤ 2n | |
2m ≤ x< 2n and 2m ≤ y ≤ n+m | |
2m ≤ x < 2n and 2m ≤ y ≤ 2n |
Best case:
First push m elements in S1 then pop m elements from S1 and push them in S2 and then pop all m elements from S2. Now push remaining (n-m) elements to S1.
So total push operation
= m + m + (n-m)
= n+m
Worst Case:
First push all n elements in S1. Then pop n elements from S1 and push them into S2. Now pop m elements from S2.
So total push operation
= n+n
= 2n
Now lets consider for pop operation, i.e., y.
For best case:
First push m elements in S1, then pop m elements and push them in S2. Now pop that m elements from S2. Now push remaining (n-m) elements in S1.
So total pop operation
= m+m
= 2m
For worst case:
First push n elements in S1, then pop them from S1 and push them into S2. Now pop m elements fro m S2.
So total pop operation
= n+m
Therefore, option A is correct answer.
Question 11 |
Double Ended Queue | |
Queue | |
Priority Queue | |
Stack |
Stack: Stack is an abstract data type that serves as a collection of elements, with two principal operations:
->push, which adds an element to the collection, and
->pop, which removes the most recently added element that was not yet removed.
Both PUSH and POP operations are done from a single end.The order in which elements come off a stack gives rise to its alternative name, LIFO (last in, first out).
Queue: a queue is a collection of entities that are maintained in a sequence and can be modified by the addition of entities at one end of the sequence and removal from the other end of the sequence. It allows addition and deletion of items from fixed different ends.
Question 12 |
3 queues | |
2 queues | |
only one queue is sufficient | |
none of the options |
Question 13 |
Doubly link list | |
Graph | |
Heap | |
Stack |
Question 14 |
operations are defined by the following code.
push(x)
A[pos] x
pos pos+1
end push
pop()
pospos+1
Return A[pos]
end pop
Which of the following will initialize an empty stack with capacity N for the above implementation?
pos ← -1 | |
pos ← 0 | |
pos ← 1 | |
pos ←N-1 |
Now if you imagine an array of length N-1, for every push the empty indices are getting decremented.
To explain in detail,
consider an empty array, so number of empty indices are N-1 ......(1)
When we push one element into it, the empty indices will reduce by 1 (i.e. decreented.)
Hence, From equation 1 we can say that pos is initialised to N-1
Question 15 |
delete a, b; and insert e,a,f; | |
insert e,a,f and delete a,b | |
insert e, delete b and insert f
| |
insert e,f, move a to place it between e and f, then delete b
|
Question 16 |
If (rear == maxsize - 1) rear=0; else rear = rear + 1; is required in
circular queue
| |
linear queue | |
stack | |
deque
|
Question 17 |
The data structure required for breadth first traversal on a graph is
queue
| |
stack
| |
array | |
tree
|
The data structure required for depth first traversal on a graph is Stack.
Question 18 |
Depth first search graph search algorithm uses ____ data structure for its implementation.
Stack
| |
Tree | |
Dequeue
| |
Queue |
Whereas Breadth first search algorithm uses queue data structure for its implementation.
Question 19 |
For implementation of recursion system uses ____ data structure.
Linked list
| |
Deque | |
Stack | |
Queue
|
Question 20 |
Queue structure is used in ____
Polynomial addition | |
Recursion
| |
Depth First search algorithm
| |
Breadth First search algorithm
|
Recursion uses stack data structure.
Depth first search algorithm uses stack data structure.
Breadth first search algorithm uses queue data structure.
Question 21 |
____ is First in last out kind of data structure.
Stack | |
Array | |
Deque
| |
Queue
|
A Queue is a linear structure which follows a particular order in which the operations are performed. The order is First In First Out (FIFO).
Question 22 |
With respect to deque which of the following is true?
Insertion is done from front end
| |
Insertion and deletion can be done at front and rear ends | |
Deletion is done from rear end
| |
Insertion is done only from rear end
|
Question 23 |
Queue | |
Stack | |
File | |
All the above |
Question 24 |
Stack | |
Binary Tree | |
Queue | |
All of the above |
