Recurrences
Question 1 |
For constants a ≥ 1 and b > 1, consider the following recurrence defined on the non-negative integers:
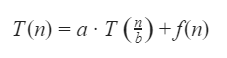
Which one of the following options is correct about the recurrence T(n)?
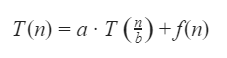
Which one of the following options is correct about the recurrence T(n)?
 | |
 | |
 | |
 |
Question 1 Explanation:

Question 2 |
For parameters a and b, both of which are ω(1), T(n) = T(n1/a)+1, and T(b)=1.
Then T(n) is
θ(loga logb n) | |
θ(logb loga n)
| |
θ(log2 log2 n)
| |
θ(logab n)
|
Question 2 Explanation:
T(n) = T(n1/a+1, T(b) = 1
T(n) = [T(n1/a2)+1] + 1
= [T(n1/a3)+1] + 2
= [T(n1/a3)] + 3
= [T(n1/ak)] + b
= logb n = ak
= log logb n = k log a
= k= loga logb n
T(n)=1+loga logb n
T(n)=O(loga logb n)
T(n) = [T(n1/a2)+1] + 1
= [T(n1/a3)+1] + 2
= [T(n1/a3)] + 3
= [T(n1/ak)] + b
= logb n = ak
= log logb n = k log a
= k= loga logb n
T(n)=1+loga logb n
T(n)=O(loga logb n)
Question 3 |
The Fibonacci sequence {f1,f2,f3,...,fn} is defined by the following recurrence:
fn+2 = fn+1 + fn, n ≥ 1; f2=1 : f1=1
Prove by induction that every third element of the sequence is even.
Theory Explanation. |
Question 4 |
The solution to the recurrence equation T(2k) = 3 T(2k-1) + 1, T(1)=1, is:
 | |
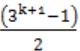 | |
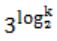 | |
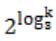 |
Question 4 Explanation:
T(2k) = 3T(2k-1) + 1
T(1)=1
k=0; T(1) = 3T(2-1)+1
k=1; T(2) = 3T(20)+1 = 3(1)+1 = 4
k=2; T(4) = 3T(21)+1 = 3(4)+1 = 13
k=3; T(8) = 3T(22)+1 = 3(13)+1 = 40
k=4; T(16) = 3T(23)+1 = 3(40)+1 = 121
Simply go through the options.
Option B:
k=4 ⇒ (34+1-1)/2
⇒ (243-1)/2
⇒ 121
T(1)=1
k=0; T(1) = 3T(2-1)+1
k=1; T(2) = 3T(20)+1 = 3(1)+1 = 4
k=2; T(4) = 3T(21)+1 = 3(4)+1 = 13
k=3; T(8) = 3T(22)+1 = 3(13)+1 = 40
k=4; T(16) = 3T(23)+1 = 3(40)+1 = 121
Simply go through the options.
Option B:
k=4 ⇒ (34+1-1)/2
⇒ (243-1)/2
⇒ 121
Question 5 |
Consider the following recurrence relation
T(1) = 1 T(n+1) = T(n) + ⌊√n+1⌋ for all n≥1
The value of T(m2) for m ≥ 1 is
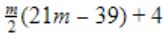 | |
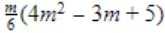 | |
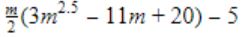 | |
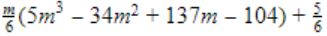 |
Question 5 Explanation:
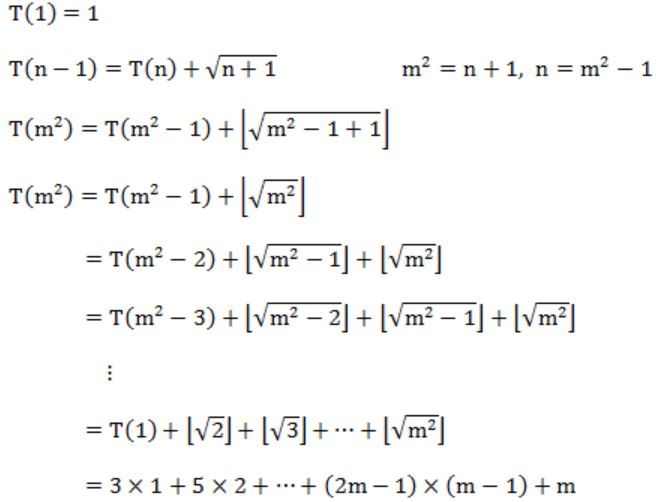
Considering floor value for square root of numbers.
Successive root number of numbers are in the series 3, 5, 7, ... like 3 numbers from 1... 4, 5 numbers 5-9 and so on.

Question 6 |
The recurrence equation
T(1) = 1 T(n) = 2T(n - 1) + n, n ≥ 2
evaluates to
2n+1 – n – 2 | |
2n – n | |
2n+1 – 2n – 2 | |
2n + n |
Question 6 Explanation:
T(1) =1
T(n) = 2T(n-1) + n
T(2) = 2T(1) + 2 = 2 + 2 = 4
T(3) = 2T(2) + n = 2(4) + 3 = 11
T(4) = 2T(3) + 4 = 22 + 4 = 26
Let check with the options:
Option A:
n=4
24+1 - 4 - 2
32 - 6
26 (✔️)
Option B:
n=4
2n-n
24-4
12(✖️)
Option C:
n=4
24+1 - 2(4) - 8
32 - 10
22(✖️)
Option D:
n=4
2n - n
24 - 4
12(✖️)
T(n) = 2T(n-1) + n
T(2) = 2T(1) + 2 = 2 + 2 = 4
T(3) = 2T(2) + n = 2(4) + 3 = 11
T(4) = 2T(3) + 4 = 22 + 4 = 26
Let check with the options:
Option A:
n=4
24+1 - 4 - 2
32 - 6
26 (✔️)
Option B:
n=4
2n-n
24-4
12(✖️)
Option C:
n=4
24+1 - 2(4) - 8
32 - 10
22(✖️)
Option D:
n=4
2n - n
24 - 4
12(✖️)
Question 7 |
(a) Use the patterns given to prove that
(You are not permitted to employ induction)

(b) Use the result obtained in (a) to prove that
Theory Explanation. |
Question 8 |
Consider the following recurrence relation:
T(n)=√nT(√n)+n for n>=1,
1 for n=1
Which one of the following options is CORRECT?
T(n)= Θ(n loglogn )
| |
T(n)=Θ(n logn) | |
T(n)=Θ(n2 logn)
| |
T(n)=Θ(n2loglogn) |
Question 9 |
The Lucas sequence Ln is defined by the recurrence relation:
Ln = Ln-1 + Ln-2 , for n >= 3,
with L1 = 1 and L2 = 3.
Which one of the options given is TRUE?
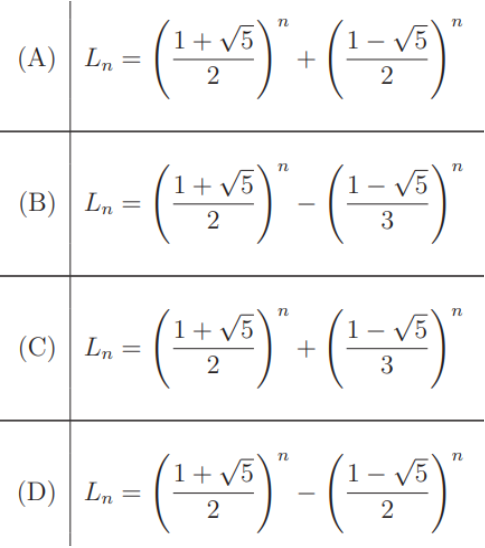
Ln = Ln-1 + Ln-2 , for n >= 3,
with L1 = 1 and L2 = 3.
Which one of the options given is TRUE?
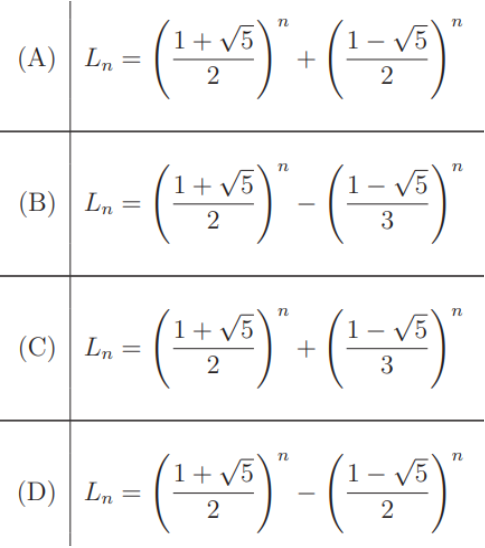
A | |
B | |
C | |
D |
Question 10 |
Let f and g be functions of natural numbers given by f(n)=n and g(n)=n2
Which of the following statements is/are TRUE?
Which of the following statements is/are TRUE?
f ∈ O(g) | |
f ∈ Ω(g) | |
f ∈ o(g) | |
f ∈ Θ(g) |
Question 11 |
Consider functions Function 1 and Function 2 expressed in pseudocode as follows:
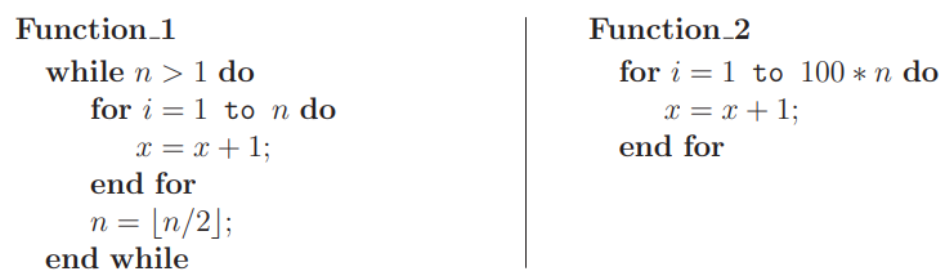
Let f1(n) and f2(n) denote the number of times the statement “x = x + 1” is executed in Function 1 and Function 2, respectively. Which of the following statements is/are TRUE?
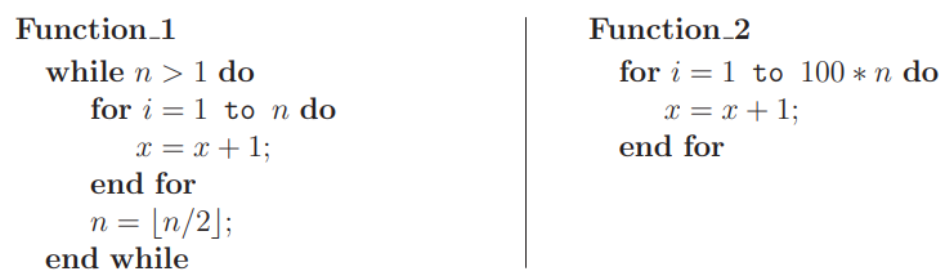
Let f1(n) and f2(n) denote the number of times the statement “x = x + 1” is executed in Function 1 and Function 2, respectively. Which of the following statements is/are TRUE?
f1(n) ε Θ(f2(n)) | |
f1(n) ε o(f2(n)) | |
f1(n) ε ω(f2(n)) | |
f1(n) ε O(n) |
Question 12 |
Let an represent the number of bit strings of length n containing two consecutive 1s. What is the recurrence relation for an?
an-2 + an-1 + 2n-2
| |
an-2 + 2an-1 + 2n-2 | |
2an-2 + an-1 + 2n-2 | |
2an-2 + 2an-1 + 2n-2 |
Question 12 Explanation:
For string of length 1, there is '0' consecutive 1's.
So, a1 = 0
For string of length 2,
a2 = 1
Similarly, a3 = 3
a4 = 8
Only (A) will satisfy the above values.
So, a1 = 0
For string of length 2,
a2 = 1
Similarly, a3 = 3
a4 = 8
Only (A) will satisfy the above values.
There are 12 questions to complete.
