Regular-Expression
Question 1 |
In some programming languages, an identifier is permitted to be a letter following by any number of letters or digits. If L and D denote the sets of letters and digits respectively, which of the following expressions defines an identifier?
(L ∪ D)+ | |
L(L ∪ D)* | |
(L⋅D)* | |
L⋅(L⋅D)* |
L(L ∪ D)*
Question 2 |
Which one of the following regular expressions represents the set of all binary strings with an odd number of 1’s?
10*(0*10*10*)*
| |
((0 + 1)*1(0 + 1)*1)*10*
| |
(0*10*10*)*10* | |
(0*10*10*)*0*1
|
The regular expression ((0+1)*1(0+1)*1)*10* generate string “11110” which is not having odd number of 1’s , hence wrong option.
The regular expression (0*10*10*)10* is not a generating string “01”. Hence this is also wrong . It seems none of them is correct.
NOTE: Option 3 is most appropriate option as it generates the max number of strings with odd 1’s.
But option 3 is not generating odd strings. So, still it is not completely correct.
The regular expression (0*10*10*)*0*1 always generates all string ends with “1” and thus does not generate string “01110” hence wrong option.
Question 3 |
Which two of the following four regular expressions are equivalent? (ε is the empty string).
- (i) (00)*(ε+0)
(ii) (00)*
(iii) 0*
(iv) 0(00)*
(i) and (ii) | |
(ii) and (iii) | |
(i) and (iii) | |
(iii) and (iv) |
In these two, we have any no. of 0's as well as null.
Question 4 |
Which one of the following regular expressions over {0,1} denotes the set of all strings not containing 100 as a substring?
0*(1+0)* | |
0*1010* | |
0*1*01 | |
0(10+1)* |
(B) generates 100 as substring.
(C) doesn't generate 1.
(D) answer.
Question 5 |
(a) An identifier in a programming language consists of upto six letters and digits of which the first character must be a letter. Derive a regular expression for the identifier.
(b) Build an LL(1) parsing table for the language defined by the LL(1) grammar with productions
Program → begin d semi X end X → d semi X | sY Y → semi s Y | ε
Theory Explanation. |
Question 6 |
The string 1101 does not belong to the set represented by
110*(0 + 1) | |
1 ( 0 + 1)* 101 | |
(10)* (01)* (00 + 11)* | |
Both C and D |
C & D are not generate string 1101.
Question 7 |
If the regular set A is represented by A = (01 + 1)* and the regular set ‘B’ is represented by B = ((01)*1*)*, which of the following is true?
A ⊂ B | |
B ⊂ A | |
A and B are incomparable | |
A = B |
Question 8 |
Let S and T be language over Σ = {a,b} represented by the regular expressions (a+b*)* and (a+b)*, respectively. Which of the following is true?
S ⊂ T | |
T ⊂ S | |
S = T | |
S ∩ T = ɸ |
Question 9 |
The regular expression 0*(10*)* denotes the same set as
(1*0)*1* | |
0+(0+10)* | |
(0+1)*10(0+1)* | |
None of the above |
Option (B) and (C) doesn't generate 11.
Question 10 |
Which of the following regular expression identifies are true?
(B) RHS generates Σ* while LHS can't generate strings where r comes after s like sr, srr, etc.
LHS ⊂ RHS.
(C) LHS generates Σ* while RHS can't generate strings where r comes after an s.
RHS ⊂ LHS.
(D) LHS contains all strings where after an s, no r comes. RHS contains all strings of either r or s but no combination of them.
So, RHS ⊂ LHS.
Question 11 |
Choose the correct alternatives (more than one may be correct) and write the corresponding letters only: Let r = 1(1+0)*, s = 11*0 and t = 1*0 be three regular expressions. Which one of the following is true?
L(s) ⊆ L(r) and L(s) ⊆ L(t) | |
L(r) ⊆ L(s) and L(s) ⊆ L(t) | |
L(s) ⊆ L(t) and L(s) ⊆ L(r) | |
L(t) ⊆ L(s) and L(s) ⊆ L(r) | |
None of the above | |
A and C |
L(s) ⊆ L(t), because 't' generates all the strings which 's' generates but 't' also generates '0' which 's' do not generates.
Question 12 |
(0+1 (01*0)*1)* | |
(0+11+10(1+00)*01)* | |
(0*(1(01*0)*1)*)* | |
(0+11+11(1+00)*00)* |
Transition table
|
0 |
1 |
|
|
->*q0 |
q0 |
q1 |
|
q1 |
q2 |
q0 |
|
q2 |
q1 |
q2 |
DFA of divisible by 3
The regular expression will be
Three paths to reach to final state from initial state
Path 1: self loop of 0 on q0
Path 2: q0->q1->q0 hence 11
Path 3: q0->q1->q2->q1->q0 hence 10(1+00)*01
So finally the regular expression will be
(0+11+10(1+00)*01)*
Other regular expression is (if we consider two paths)
Path 1: Path 1: self loop of 0 on q0
Path 2: q0->q1->q2*->q1->q0
Hence regular expression
(0+1 (01*0)*1)*
Another regular expression is (if we consider only one path and remaining part is present inside this path as cycles)
q0->q1->q2->q1->q0
Another regular expression is
(0*(1(01*0)*1)*)*
So A,B, C are correct.
Option D generates string 11100 which is not accepted by FA hence wrong.
Question 13 |
Which one of the following regular expressions is NOT equivalent to the regular expression (a + b + c)*?
(a* + b* + c*)* | |
(a*b*c*)* | |
((ab)* + c*)* | |
(a*b* + c*)* |
From option 'c' we cannot be able to create a without b. So option is not equivalent.
Question 14 |
44 | |
Question 15 |
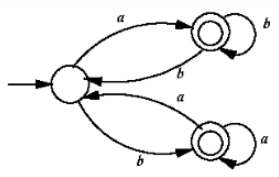
Which regular expression best describes the language accepted by the non-deterministic automaton below?
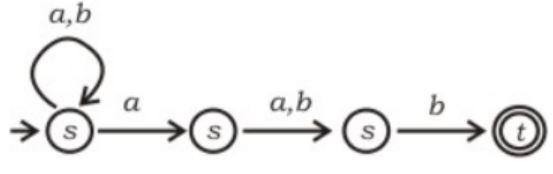
(a + b)* a(a + b)b | |
(abb)* | |
(a + b)* a(a + b)* b(a + b)* | |
(a + b)* |
Question 16 |
Consider the regular expression
R = (a + b)* (aa + bb) (a + b)*Which of the following non-deterministic finite automata recognizes the language defined by the regular expression R? Edges labeled λ denote transitions on the empty string.
 | |
 | |
 | |
 |
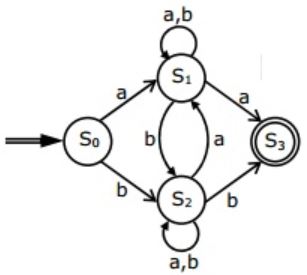But option (B), (C), (D) accepts aba, which do not contain aa or bb as substring.
Hence, (A) is correct.
Question 17 |
Consider the regular expression
R = (a + b)* (aa + bb) (a + b)*Which deterministic finite automaton accepts the language represented by the regular expression R ?
 | |
 | |
 | |
 |
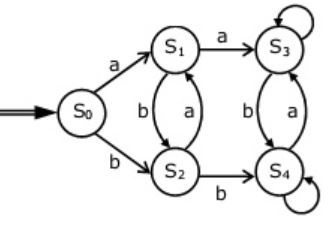(C) It is not accepting 'abb' which is in language.
(D) It is not accepting 'aa' and 'bb' which is in language.
Question 18 |
Consider the regular expression
R = (a + b)* (aa + bb) (a + b)*Which one of the regular expressions given below defines the same language as defined by the regular expression R?
(a(ba)* + b(ab)*)(a + b)+ | |
(a(ba)* + b(ab)*)*(a + b)* | |
(a(ba)* (a + bb) + b(ab)*(b + aa))(a + b)* | |
(a(ba)* (a + bb) + b(ab)*(b + aa))(a + b)+ |
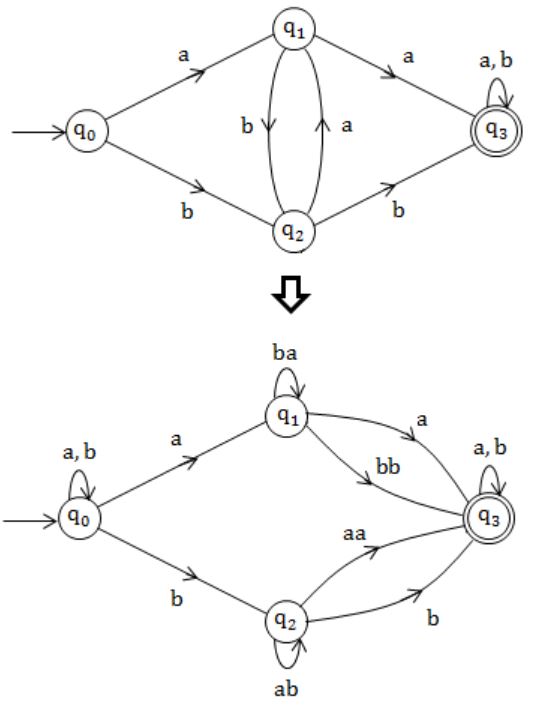
Having NFA:
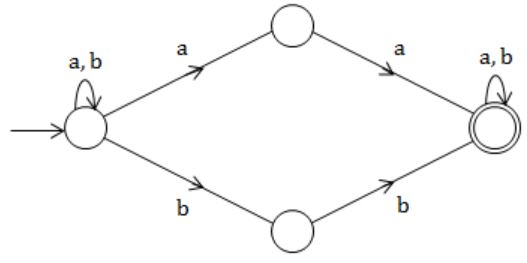
Equivalent DFA:
