Theory-of-Computation
Question 1 |
A | (0+1 (01*0)*1)* |
B | (0+11+10(1+00)*01)* |
C | (0*(1(01*0)*1)*)* |
D | (0+11+11(1+00)*00)* |
Transition table
|
0 |
1 |
|
|
->*q0 |
q0 |
q1 |
|
q1 |
q2 |
q0 |
|
q2 |
q1 |
q2 |
DFA of divisible by 3

The regular expression will be
Three paths to reach to final state from initial state
Path 1: self loop of 0 on q0
Path 2: q0->q1->q0 hence 11
Path 3: q0->q1->q2->q1->q0 hence 10(1+00)*01
So finally the regular expression will be
(0+11+10(1+00)*01)*
Other regular expression is (if we consider two paths)
Path 1: Path 1: self loop of 0 on q0
Path 2: q0->q1->q2*->q1->q0
Hence regular expression
(0+1 (01*0)*1)*
Another regular expression is (if we consider only one path and remaining part is present inside this path as cycles)
q0->q1->q2->q1->q0
Another regular expression is
(0*(1(01*0)*1)*)*
So A,B, C are correct.
Option D generates string 11100 which is not accepted by FA hence wrong.
Question 2 |
A | L={w x wR xR | w, x ∈ {0,1}* } |
B | L={w wR x xR | w, x ∈ {0,1}* } |
C | L={w x xR wR | w, x ∈ {0,1}* } |
D | L={w x wR | w, x ∈ {0,1}* } |
Option A: L={w x wR xR | w, x ∈ {0,1}* }
This is not CFL as if we push “w” then “x” then we cannot match wR with “w” as top of stack contains x.
Option B: L={w wR x xR | w, x ∈ {0,1}* }
This is CFL. We non deterministically guess the middle of the string. So we push “w” then match with wR and again push x and match with xR
Option C: L={w x xR wR | w, x ∈ {0,1}* }
This is also CFL. We non deterministically guess the middle of the string. So we push “w” then push x and then match with xR and again match with wR
Option D: L={w x wR | w, x ∈ {0,1}* }
This is a regular language (hence CFL). In this language every string start and end with same symbol (as x can expand).
Question 3 |
- Consider the following two statements about regular languages:
S1: Every infinite regular language contains an undecidable language as a subset.
S2: Every finite language is regular.
Which one of the following choices is correct.?
A | Only S2is true. |
B | Both S1and S2are true. |
C | Only S1is true. |
D | Neither S1nor S2is true. |
-
S1 is true. We can solve this intuitively.
Suppose L=(a+b)* i.e, sigma*
We know that this is a regular language and any language is subset of this language.
As we know so many undecidable languages (not recursive languages) exist, hence S1 is true.
Take another example:
L=a* which is regular and infinite.
Take its subset L1=an | n> 0 and n is a set such that it cannot be generated by any algorithm
I.e, n is a set of natural numbers which does not have any algorithm which can generate this
So L1 is a undecidable language.
L2 is true as every finite language is regular.
Question 4 |
A | L U {01} |
B | L.L |
C | {0,1}*-L |
D | L-{01} |
Question 5 |
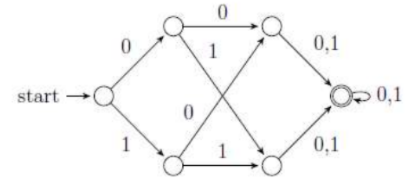
The number of strings of length 8 accepted by the above automaton is __________.
A | 256 |
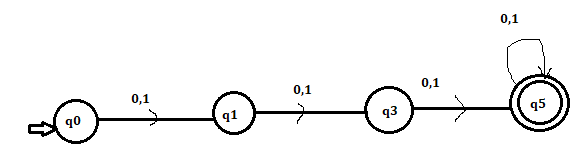
So the DFA accepts all strings of length greater than equal to 3.
For 8 length strings we have 8 positions
_ _ _ _ _ _ _ _
For each position there are two possibilities 0 or 1.
So for 8 positions we have 28 possibilities = 256
Question 6 |
A | 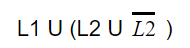 |
B | 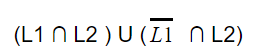 |
C | 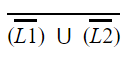 |
D | 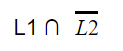 |

Question 7 |
Input sequence: 00100011000011100
Output sequence: 00000001000001100
A Mealy Machine is a state machine where both the next state and the output are functions of the present state and the current input.
The above mentioned circuit can be designed as a two-state Mealy machine. The states in the Mealy machine can be represented using Boolean values 0 and 1. We denote the current state, the next state, the next incoming bit, and the output bit of the Mealy machine by the variables s, t, b and y respectively.
What are the Boolean expressions corresponding to t and y in terms of s and b?
A | 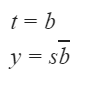 |
B | 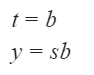 |
C | 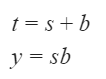 |
D | 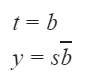 |
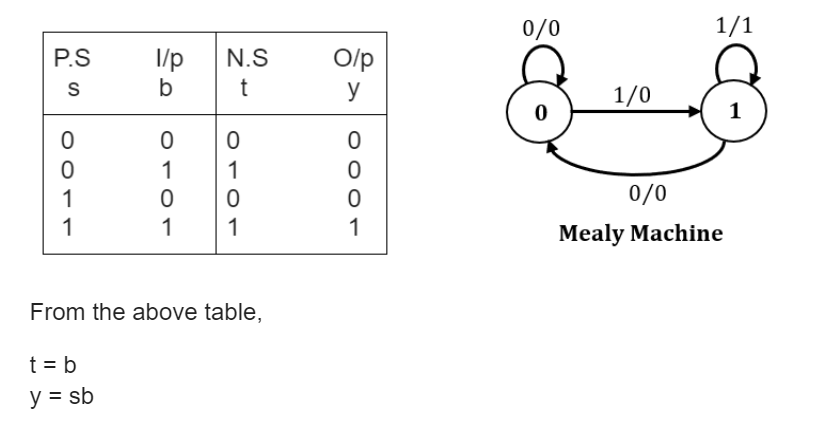
Question 8 |
In some programming languages, an identifier is permitted to be a letter following by any number of letters or digits. If L and D denote the sets of letters and digits respectively, which of the following expressions defines an identifier?
A | (L ∪ D)+ |
B | L(L ∪ D)* |
C | (L⋅D)* |
D | L⋅(L⋅D)* |
L(L ∪ D)*
Question 9 |
Consider a grammar with the following productions
S → a∝b|b∝c| aB S → ∝S|b S → ∝b b|ab S ∝ → bd b|b
The above grammar is:
A | Context free |
B | Regular |
C | Context sensitive |
D | LR(k) |
Because LHS must be single non-terminal symbol.
S ∝→ b [violates CSG]
→ Length of RHS production must be atleast same as that of LHS.
Extra information is added to the state by redefining iteams to include a terminal symbol as second component in this type of grammar.
Ex: [A → αβa]
A → αβ is a production, a is a terminal (or) right end marker $, such an object is called LR(k).
So, answer is (D) i.e., LR(k).
Question 10 |
Which of the following definitions below generates the same language as L, where L = {xnyn such that n >= 1}?
I. E → xEy|xy II. xy|(x+xyy+) III. x+y+
A | I only |
B | I and II |
C | II and III |
D | II only |
Question 11 |
A finite state machine with the following state table has a single input x and a single out z.
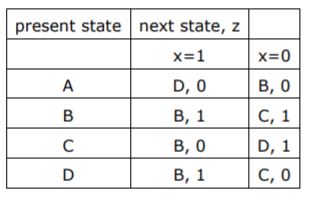
If the initial state is unknown, then the shortest input sequence to reach the final state C is:
A | 01 |
B | 10 |
C | 101 |
D | 110 |
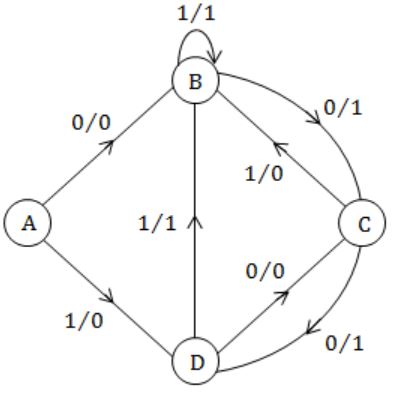
If A is the start state, shortest sequence is 10 'or' 00 to reach C.
If B is the start state, shortest sequence is 0 to reach C.
If C is the start state, shortest sequence is 10 or 00 to reach C.
If D is the start state, shortest sequence is 0 to reach C.
∴ (B) is correct.
Question 12 |
Let Σ = {0,1}, L = Σ* and R = {0n1n such that n >0} then the languages L ∪ R and R are respectively
A | regular, regular |
B | not regular, regular |
C | regular, not regular |
D | not regular, no regular |
Question 13 |
Let L be a language over ∑ i.e., *L ≤ ∑ . Suppose L satisfies the two conditions given below
(i) L is in NP and
(ii) For every n, there is exactly one string of length n that belongs to L.
Let Lc be the complement of L over ∑*. Show that Lc is also in NP.
A | Theory Explanation. |
Question 14 |
Consider the language L = {an| n≥0} ∪ {anbn| n≥0} and the following statements.
- I. L is deterministic context-free.
II. L is context-free but not deterministic context-free.
III. L is not LL(k) for any k.
Which of the above statements is/are TRUE?
A | II only |
B | III only |
C | I only |
D | I and III only |
We can make DPDA for this.

L is not LL(k) for any “k” look aheads. The reason is the language is a union of two languages which have common prefixes. For example strings {aa, aabb, aaa, aaabbb,….} present in language. Hence the LL(k) parser cannot parse it by using any lookahead “k” symbols.
Question 15 |
Consider the following statements.
- I. If L1 ∪ L2 is regular, then both L1 and L2 must be regular.
II. The class of regular languages is closed under infinite union.
Which of the above statements is/are TRUE?
A | Both I and II
|
B | II only |
C | Neither I nor II |
D | I only
|
Assume L1 = {an bn | n>0} and L2 = complement of L1
L1 and L2 both are DCFL but not regular, but L1 U L2 = (a+b)* which is regular.
Hence even though L1 U L2 is regular, L1 and L2 need not be always regular.
Statement II is wrong.
Assume the following finite (hence regular) languages.
L1 = {ab}
L2 = {aabb}
L3 = {aaabbb}
.
.
.
L100 = {a100 b100}
.
.
.
If we take infinite union of all above languages i.e,
{L1 U L2 U ……….L100 U ……}
then we will get a new language L = {an bn | n>0}, which is not regular.
Hence regular languages are not closed under infinite UNION.
Question 16 |
Which one of the following regular expressions represents the set of all binary strings with an odd number of 1’s?
A | 10*(0*10*10*)*
|
B | ((0 + 1)*1(0 + 1)*1)*10*
|
C | (0*10*10*)*10* |
D | (0*10*10*)*0*1
|
The regular expression ((0+1)*1(0+1)*1)*10* generate string “11110” which is not having odd number of 1’s , hence wrong option.
The regular expression (0*10*10*)10* is not a generating string “01”. Hence this is also wrong . It seems none of them is correct.
NOTE: Option 3 is most appropriate option as it generates the max number of strings with odd 1’s.
But option 3 is not generating odd strings. So, still it is not completely correct.
The regular expression (0*10*10*)*0*1 always generates all string ends with “1” and thus does not generate string “01110” hence wrong option.
Question 17 |
Which of the following languages are undecidable? Note that
- L1 =
L2 = {
L3 = {
L4 = {
A | L2 and L3 only
|
B | L1 and L3 only
|
C | L2, L3 and L4 only |
D | L1, L3 and L4 only |
Only L3 is decidable. We can check whether a given TM reach state q in exactly 100 steps or not. Here we have to check only upto 100 steps, so here is not any case of going to infinite loop.
Question 18 |
Consider the following language.
L = {x ∈ {a,b}* | number of a’s in x is divisible by 2 but not divisible by 3}
The minimum number of states in a DFA that accepts L is ______.
A | 6 |
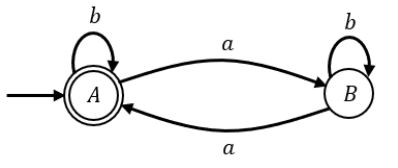
DFA 1: No. of a’s not divisible by 3
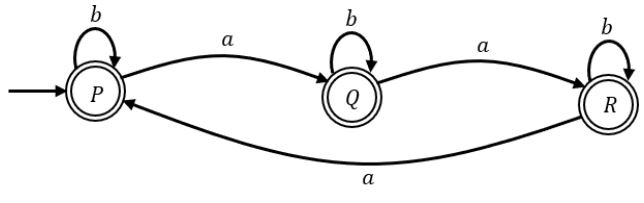
Using product automata:

Question 19 |
Consider the following languages.
- L1 = {wxyx | w,x,y ∈ (0 + 1)+}
L2 = {xy | x,y ∈ (a + b)*, |x| = |y|, x ≠ y}
Which one of the following is TRUE?
A | L1 is context-free but not regular and L2 is context-free. |
B | Neither L1 nor L2 is context-free.
|
C | L1 is regular and L2 is context-free.
|
D | L1 is context-free but L2 is not context-free. |
So it is equivalent to
(a+b)+ a (a+b)+ a + (a+b)+ b (a+b)+ b
L2 is CFL since it is equivalent to complement of L=ww.
Complement of L=ww is CFL.
Question 20 |
Which two of the following four regular expressions are equivalent? (ε is the empty string).
- (i) (00)*(ε+0)
(ii) (00)*
(iii) 0*
(iv) 0(00)*
A | (i) and (ii) |
B | (ii) and (iii) |
C | (i) and (iii) |
D | (iii) and (iv) |
In these two, we have any no. of 0's as well as null.
Question 21 |
Which of the following statements is false?
A | The Halting problem of Turing machines is undecidable. |
B | Determining whether a context-free grammar is ambiguous is undecidbale. |
C | Given two arbitrary context-free grammars G1 and G2 it is undecidable whether L(G1) = L(G2). |
D | Given two regular grammars G1 and G2 it is undecidable whether L(G1) = L(G2). |
1) Membership
2) Emtiness
3) Finiteness
4) Equivalence
5) Ambiguity
6) Regularity
7) Everything
8) Disjointness
All are decidable for Regular languages.
→ First 3 for CFL.
→ Only 1st for CSL and REC.
→ None for RE.
Question 22 |
Let L ⊆ Σ* where Σ = {a, b}. Which of the following is true?
A | L = {x|x has an equal number of a's and b's } is regular |
B | L = {anbn|n≥1} is regular |
C | L = {x|x has more a's and b's} is regular |
D | L = {ambn|m ≥ 1, n ≥ 1} is regular |
Here, m and n are independent.
So 'L' Is Regular.
Question 23 |
If L1 and L2 are context free languages and R a regular set, one of the languages below is not necessarily a context free language. Which one?
A | L1, L2 |
B | L1 ∩ L2 |
C | L1 ∩ R |
D | L1 ∪ L2 |
Question 24 |
Define for a context free language L ⊆ {0,1}*, init(L) = {u ∣ uv ∈ L for some v in {0,1}∗} (in other words, init(L) is the set of prefixes of L)
Let L = {w ∣ w is nonempty and has an equal number of 0’s and 1’s}
Then init(L) is
A | the set of all binary strings with unequal number of 0’s and 1’s |
B | the set of all binary strings including the null string |
C | the set of all binary strings with exactly one more 0’s than the number of 1’s or one more 1 than the number of 0’s |
D | None of the above |
Question 25 |
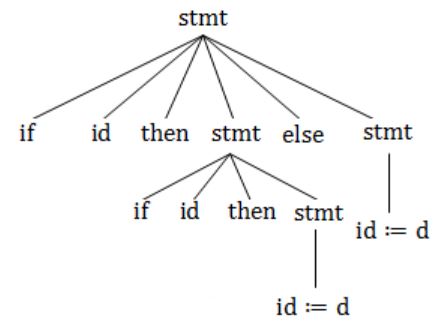
The grammar whose productions are
→ if id then → if id then else → id := id
is ambiguous because
A | the sentence if a then if b then c:=d |
B | the left most and right most derivations of the sentence if a then if b then c:=d give rise top different parse trees |
C | the sentence if a then if b then c:=d else c:=f has more than two parse trees |
D | the sentence if a then if then c:=d else c:=f has two parse trees |
"if a then if b then c:=d else c:=f".
Parse tree 1:

Parse tree 2:
Question 26 |
Consider the given figure of state table for a sequential machine. The number of states in the minimized machine will be
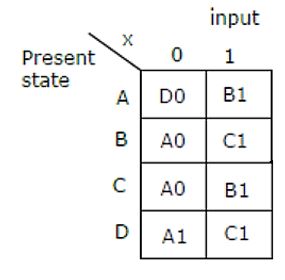
A | 4 |
B | 3 |
C | 2 |
D | 1 |
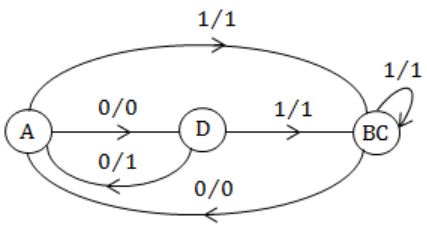
Question 27 |
Let G be a context-free grammar where G = ({S, A, B, C},{a,b,d},P,S) with the productions in P given below.
S → ABAC A → aA ∣ ε B → bB ∣ ε C → d
(ε denotes null string). Transform the grammar G to an equivalent context-free grammar G' that has no ε productions and no unit productions. (A unit production is of the form x → y, and x and y are non terminals.)
A | Theory Explanation. |
Question 28 |
Let Q = ({q1,q2}, {a,b}, {a,b,Z}, δ, Z, ϕ) be a pushdown automaton accepting by empty stack for the language which is the set of all non empty even palindromes over the set {a,b}. Below is an incomplete specification of the transitions δ. Complete the specification. The top of the stack is assumed to be at the right end of the string representing stack contents.
(1) δ(q1,a,Z) = {(q1,Za)}
(2) δ(q1,b,Z) = {(q1,Zb)}
(3) δ(q1,a,a) = {(.....,.....)}
(4) δ(q1,b,b) = {(.....,.....)}
(5) δ(q2,a,a) = {(q2,ϵ)}
(6) δ(q2,b,b) = {(q2,ϵ)}
(7) δ(q2,ϵ,Z) = {(q2,ϵ)} A | Theory Explanation. |
Question 29 |
Given Σ = {a,b}, which one of the following sets is not countable?
A | Set of all strings over Σ |
B | Set of all languages over Σ |
C | Set of all regular languages over Σ |
D | Set of all languages over Σ accepted by Turing machines |
Question 30 |
Which one of the following regular expressions over {0,1} denotes the set of all strings not containing 100 as a substring?
A | 0*(1+0)* |
B | 0*1010* |
C | 0*1*01 |
D | 0(10+1)* |
(B) generates 100 as substring.
(C) doesn't generate 1.
(D) answer.
Question 31 |
Which one of the following is not decidable?
A | Given a Turing machine M, a stings s and an integer k, M accepts s within k steps |
B | Equivalence of two given Turing machines |
C | Language accepted by a given finite state machine is not empty |
D | Language generated by a context free grammar is non empty |
In (A) the number of steps is restricted to a finite number 'k' and simulating a TM for 'k' steps is trivially decidable because we just go to step k and output the answer.
(B) Equivalence of two TM's is undecidable.
For options (C) and (D) we do have well defined algorithms making them decidable.
Question 32 |
Which of the following languages over {a,b,c} is accepted by a deterministic pushdown automata?
Note: wR is the string obtained by reversing 'w'.
A | {w⊂wR|w ∈ {a,b}*} |
B | {wwR|w ∈ {a,b,c}*} |
C | {anbncn|n ≥ 0} |
D | {w|w is a palindrome over {a,b,c}} |
(B) wwR, is realized by NPDA because we can't find deterministically the center of palindrome string.
(C) {anbncn | n ≥ 0} is CSL.
(D) {w | w is palindrome over {a,b,c}},
is realized by NPDA because we can't find deterministically the center of palindrome string.
Question 33 |
Let N be an NFA with n states. Let k be the number of states of a minimal DFA which is equivalent to N. Which one of the following is necessarily true?
A | k ≥ 2n |
B | k ≥ n |
C | k ≤ n2 |
D | k ≤ 2n
|
In other words, if number of states in NFA is “n” then the corresponding DFA have at most 2n states.
Hence k ≤ 2n is necessarily true.
Question 34 |
The set of all recursively enumerable languages is
A | closed under complementation. |
B | closed under intersection. |
C | a subset of the set of all recursive languages. |
D | an uncountable set. |
Recursive enumerable languages are not closed under Complementation.
Recursive enumerable languages are a countable set, as every recursive enumerable language has a corresponding Turing Machine and set of all Turing Machine is countable.
Recursive languages are subset of recursive enumerable languages.
Question 35 |
L0 = {ε}
Li = Li-1∙L for all i>0
The order of a language L is defined as the smallest k such that Lk = Lk+1.
Consider the language L1 (over alphabet 0) accepted by the following automaton.
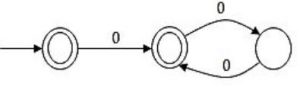
The order of L1 is ______.
A | 2 |
B | 3 |
C | 4 |
D | 5 |
Now L10 = ϵ and L11 = ϵ . (ϵ+0 (00)*) = ϵ + 0 (00)* = L1
Now L12 = L11 .
L1 = L1 .
L1 = (ϵ + 0 (00)*) (ϵ + 0 (00)*)
= (ϵ + 0 (00)* + 0(00)* + 0(00)*0(00)*)
= (ϵ + 0 (00)* + 0(00)*0(00)* ) = 0*
As it will contain epsilon + odd number of zero + even number of zero, hence it is 0*
Now L13 = L12 .
L1 = 0* (ϵ + 0 (00)*) = 0* + 0*0(00)* = 0*
Hence L12 = L13
Or L12 = L12+1 ,
hence the smallest k value is 2.
Question 36 |
I. {am bn cp dq ∣ m + p = n + q, where m, n, p, q ≥ 0}
II. {am bn cp dq ∣ m = n and p = q, where m, n, p, q ≥ 0}
III. {am bn cp dq ∣ m = n = p and p ≠ q, where m, n, p, q ≥ 0}
IV. {am bn cp dq ∣ mn = p + q, where m, n, p, q ≥ 0}
Which of the above languages are context-free?
A | I and IV only |
B | I and II only |
C | II and III only |
D | II and IV only |
m-n = q-p
First we will push a’s in the stack then we will pop a’s after watching b’s.
Then some of a’s might left in the stack.
Now we will push c’s in the stack and then pop c’s by watching d’s.
And then the remaining a’s will be popped off the stack by watching some more d’s.
And if no d’s is remaining and the stack is empty then the language is accepted by CFG.
ii) am bn cp dq | m=n, p=q
Push a’s in stack. Pop a’s watching b’s.
Now push c’s in stack.
Pop c’s watching d’s.
So it is context free language.
iii) am bn cp dq | m=n=p & p≠q
Here three variables are dependent on each other. So not context free.
iv) Not context free because comparison in stack can’t be done through multiplication operation.
Question 37 |
(I) For an unrestricted grammar G and a string w, whether w∈L(G)
(II) Given a Turing machine M, whether L(M) is regular
(III) Given two grammar G1 and G2 whether L(G1) = L(G2)
(IV) Given an NFA N, whether there is a deterministic PDA P such that N and P accept the same language
Which one of the following statement is correct?
A | Only I and II are undecidable |
B | Only III is undecidable |
C | Only II and IV are undecidable |
D | Only I, II and III are undecidable |
I, II and III is undecidable.
Question 38 |
If the regular set A is represented by A = (01 + 1)* and the regular set ‘B’ is represented by B = ((01)*1*)*, which of the following is true?
A | A ⊂ B |
B | B ⊂ A |
C | A and B are incomparable |
D | A = B |
Question 39 |
Both A and B are equal, which generates strings over {0,1}, while 0 is followed by 1.
A | The numbers 1, 2, 4, 8, ……………., 2n, ………… written in binary |
B | The numbers 1, 2, 4, ………………., 2n, …………..written in unary |
C | The set of binary string in which the number of zeros is the same as the number of ones |
D | The set {1, 101, 11011, 1110111, ………..} |
10, 100, 1000, 10000 .... = 10*
which is regular and recognized by deterministic finite automata.
Question 40 |
Regarding the power of recognition of languages, which of the following statements is false?
A | The non-deterministic finite-state automata are equivalent to deterministic finite-state automata. |
B | Non-deterministic Push-down automata are equivalent to deterministic Push- down automata. |
C | Non-deterministic Turing machines are equivalent to deterministic Push-down automata. |
D | Both B and C |
C: Power (TM) > NPDA > DPDA.
Question 41 |
The string 1101 does not belong to the set represented by
A | 110*(0 + 1) |
B | 1 ( 0 + 1)* 101 |
C | (10)* (01)* (00 + 11)* |
D | Both C and D |
C & D are not generate string 1101.
Question 42 |
How many sub strings of different lengths (non-zero) can be found formed from a character string of length n?
A | n |
B | n2 |
C | 2n |
D |  |
Possible sub-strings are = {A, P, B, AP, PB, BA, APB}
Go through the options.
Option D:
n(n+1)/2 = 3(3+1)/2 = 6
Question 43 |
Let L be the set of all binary strings whose last two symbols are the same. The number of states in the minimum state deterministic finite 0 state automaton accepting L is
A | 2 |
B | 5 |
C | 8 |
D | 3 |

Equivalent DFA:
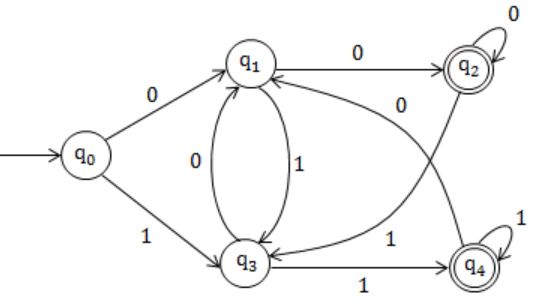
Hence, 5 states.
Question 44 |
Which of the following statements is false?
A | Every finite subset of a non-regular set is regular |
B | Every subset of a regular set is regular |
C | Every finite subset of a regular set is regular |
D | The intersection of two regular sets is regular |
Question 45 |
Design a deterministic finite state automaton (using minimum number of states) that recognizes the following language:
L = {w ∈ {0,1}* | w interpreted as a binary number (ignoring the leading zeros) is divisible by 5}
A | Theory Explanation. |
Question 46 |
Let M = ({q0, q1}, {0, 1}, {z0, x}, δ, q0, z0, ∅) be a pushdown automaton where δ is given by
- δ(q0, 1, z0) = {(q0, xz0)}
δ(q0, ε, z0) = {(q0, ε)}
δ(q0, 1, X) = {(q0, XX)}
δ(q1, 1, X) = {(q1, ε)}
δ(q0, 0, X) = {(q1, X)}
δ(q0, 0, z0) = {(q0, z0)}
(a) What is the language accepted by this PDA by empty stack?
(b) Describe informally the working of the PDA.
A | Theory Explanation. |
Question 47 |
(a) Let G1 = (N, T, P, S1) be a CFG where,
N = {S1, A, B}, T = {a,b} and
P is given by
S1 → aS1b S1 → aBb
S1 → aAb B → Bb
A → aA B → b
A → a
What is L(G1)?
(b) Use the grammar in part(a) to give a CFG
for L2 = {ai bj ak bl | i, j, k, l ≥ 1, i=j or k=l} by adding not more than 5 production rule.
(c) Is L2 inherently ambiguous?
A | Theory Explanation. |
Question 48 |
(a) An identifier in a programming language consists of upto six letters and digits of which the first character must be a letter. Derive a regular expression for the identifier.
(b) Build an LL(1) parsing table for the language defined by the LL(1) grammar with productions
Program → begin d semi X end X → d semi X | sY Y → semi s Y | ε
A | Theory Explanation. |
Question 49 |
Consider the regular expression (0 + 1) (0 + 1)…. N times. The minimum state finite automation that recognizes the language represented by this regular expression contains
A | n states |
B | n + 1 states |
C | n + 2 states |
D | None of the above |
DFA:

So, DFA requires (n+2) state.
NFA:

So, NFA requires (n+1) state.
So, final answer will be,
min(n+1, n+2)
= n+1
Question 50 |
Context-free languages are closed under:
A | Union, intersection |
B | Union, Kleene closure |
C | Intersection, complement |
D | Complement, Kleene closure |
By checking the options only option B is correct.
