Relations-and-Functions
Question 1 |

19 |

Question 2 |
Let f be a function defined by
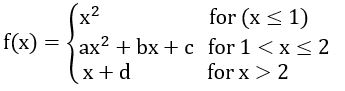
Find the values for the constants a, b, c and d so that f is continuous and differentiable every where on the real line.
Theory Explanation. |
Question 3 |
Let F be the collection of all functions f: {1,2,3} → {1,2,3}. If f and g ∈ F, define an equivalence relation ~ by f ~ g if and only if f(3) = g(3).
a) Find the number of equivalence classes defined by ~.
b) Find the number of elements in each equivalence class.
Theory Explanation. |
Question 4 |
(a) Mr. X claims the following:
If a relation R is both symmetric and transitive, then R is reflexive. For this, Mr. X offers the following proof:
"From xRy, using symmetry we get yRy. Now because R is transitive, xRy and yRy together imply xRx. Therefore, R is reflexive."
Briefly point out the flaw in Mr. X's proof.
(b) Give an example of relation R which is symmetric and transitive but not reflexive.
Theory Explanation |
Question 5 |
Every element a of some ring (R,+,0) satisfies the equation aoa = a.
Decide whether or not the ring is commutative.
Theory Explanation. |
Question 6 |
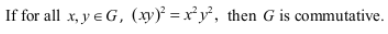 | |
 | |
If the order of G is 2 , then G is commutative. | |
If G is commutative, then a subgroup of G need not be commutative. |
(B) : False. In a multiple instance graph, a cycle always does not indicate deadlock.
(C) : False. Unsafe state may or may not lead to deadlock.
(D) : True. Since every edge is allocated, that means there are no requests. Hence, cycle is not possible.
Question 7 |
f(x) = x3 + 15x2 − 33x − 36
be a real-valued function.
Which of the following statements is/are TRUE?
f(x) does not have a local maximum | |
f(x) has a local maximum | |
f(x) does not have a local minimum | |
f(x) has a local minimum |
