Turing-machines
Question 1 |
Consider the following problem X.
Given a Turing machine M over the input alphabet Σ, any state q of M And a word w∈Σ*, does the computation of M on w visit the state q?
Which of the following statements about X is correct?
X is decidable | |
X is undecidable but partially decidable | |
X is undecidable and not even partially decidable | |
X is not a decision problem |
Question 2 |
Let a decision problem X be defined as follows:
X: Given a Turing machine M over Σ and nay word w ∈ Σ,
does M loop forever on w?
You may assume that the halting problem of Turing machine is undecidable but partially decidable.
- (a) Show that X is undecidable.
(b) Show that X is not even partially decidable.
Theory Explanation is given below. |
Question 3 |
The aim of the following question is to prove that the language {M| M is the code of a Turing Machine which, irrespective of the input, halts and outputs a 1}, is undecidable. This is to be done by reducing form the language {M',x| M' halts on x}, which is known to be undecidable. In parts (a) and (b) describe the 2 main steps in the construction of M. in part (c) describe the key property which relates the behaviour of M on its input w to the behaviour of M′ on x.
- (a) On input w, what is the first step that M must make?
(b) On input w, based on the outcome of the first step, what is the second step that M must make?
(c) What key property relates the behaviour of M on w to the behaviour of M′ on x?
Theory Explanation is given below. |
Question 4 |
(a) Show that Turing machines, which have a read only input tape and constant size work tape, recognize precisely the class or regular languages.
(b) Let L be the language of all binary strings in which the third symbol from the right is a1. Give a non-deterministic finite automaton that recognizes L. How many states does the minimized equivalent deterministic finite automaton have? Justify your answer briefly?
Theory Explanation. |
Question 5 |
Given two Turing machines M1 and M2, decide if L(M1)=L(M2). | |
Given a Turing machine M, decide if L(M) is regular. | |
Given a Turing machine M, decide if M accepts all strings. | |
Given a Turing machine M, decide if M takes more than 1073 steps on every string. |
Checking whether a Turing machine accepts a regular language is also undecidable.
Completeness problem for recursively enumerable language is undecidable thus whether a Turing Machine accepts all strings is undecidable.
Whether a Turing machine takes more than 1073 steps is decidable as we need to run the Turing Machine only for 1073 steps so no chance of going into an infinite loop hence it is decidable.
Question 6 |
A is recursive if both A and its complement are accepted by Turing machines.
True | |
False |
Question 7 |
A single tape Turing Machine M has two states q0 and q1, of which q0 is the starting state. The tape alphabet of M is {0, 1, B} and its input alphabet is {0, 1}. The symbol B is the blank symbol used to indicate end of an input string. The transition function of M is described in the following table.
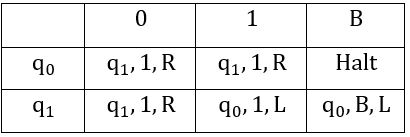
The table is interpreted as illustrated below. The entry (q1, 1, R) in row q0 and column 1 signifies that if M is in state q0 and reads 1 on the current tape square, then it writes 1 on the same tape square, moves its tape head one position to the right and transitions to state q1.
Which of the following statements is true about M?
M does not halt on any string in (0+1)+
| |
M does not halt on any string in (00+1)* | |
M halts on all strings ending in a 0 | |
M halts on all strings ending in a 1 |
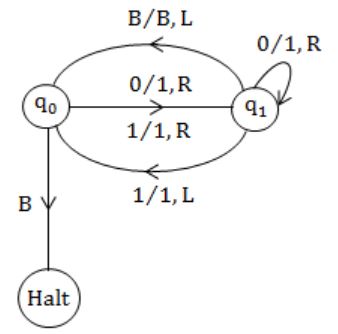
Try for any string, it will not Halt for any string other than ϵ. Hence, option (A) is correct.
