topic - solutions adda

Graphs-and-Tree

Please wait while the activity loads.
If this activity does not load, try refreshing your browser. Also, this page requires javascript. Please visit using a browser with javascript enabled.

If loading fails, click here to try again

Question 1

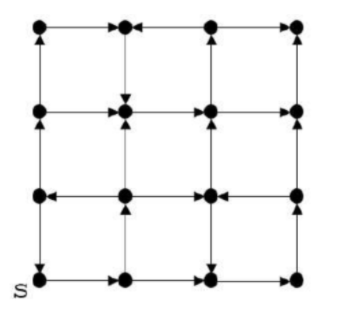
Consider the following directed graph:

Which of the following is/are correct about the graph?

A	For each pair of vertices u and v, there is a directed path from u to v.
B	The graph does not have a strongly connected component.
C	The graph does not have a topological order.
D	A depth-first traversal staring at vertex S classifies three directed edges as back edges.

Data-StructuresGraphs-and-TreeGATE 2021 CS-Set-2Video-Explanation

Question 1 Explanation:

Option-1: FALSE: There is no path from top right corner vertex to any other vertex

Option-2: FALSE: A directed graph is called strongly connected if there is a path in each direction between each pair of vertices of the graph. As there is no path from the above vertex then this statement is wrong.

Option-3: TRUE: This graph does have directed cycles, thus topological order can not be possible for according to topological definition.

Question 2

Let G = (V,E) be a directed, weighted graph with weight function w:E → R. For some function f:V → R, for each edge (u,v) ∈ E, define w'(u,v) as w(u,v) + f(u) - f(v).
Which one of the options completes the following sentence so that it is TRUE?

“The shortest paths in G under w are shortest paths under w’ too, _______”.

A	if and only if f(u) is the distance from s to u in the graph obtained by adding a new vertex s to G and edges of zero weight from s to every vertex of G
B	if and only if ∀u ∈ V, f(u) is positive
C	if and only if ∀u ∈ V, f(u) is negative
D	for every f: V→R

Data-StructuresGraphs-and-TreeGATE 2020Video-Explanation

Question 2 Explanation:

Question 3

Consider the following statements.
S₁:The sequence of procedure calls corresponds to a preorder traversal of the activation tree.
S₂:The sequence of procedure returns corresponds to a postorder traversal of the activation tree.
Which one of the following options is correct?

A	S₁is false and S₂is false
B	S₁is true and S₂is true
C	S₁is true and S₂is false
D	S₁is false and S₂is true

Data-StructuresGraphs-and-TreeGATE 2021 CS-Set-1Video-Explanation

Question 3 Explanation:

The given statements are true, they are well known facts.

The sequence of procedure calls corresponds to a preorder traversal of the activation tree.
The sequence of returns corresponds to a postorder traversal of the activation tree.

Question 4

A_____takes a directed ______ graph G and produce a linear ordering of all its vertices such that for every directed edge in G, the vertex v comes before the vertex w in the ordering.

A	Breadth first search; acyclic
B	Topological sort; acyclic
C	Breadth first search; cyclic
D	Topological sort; cyclic

Data-StructuresGraphs-and-TreeCIL Part - B

Question 4 Explanation:

Topological sorting of vertices of a Directed Acyclic Graph is an ordering of the vertices V1,v2,...vn in such a way, that if there is an edge directed towards vertex vj from vertex vi , then vi comes before vj

Question 5

Consider the following statements: A) Any tree is 2-colorable B) A graph G has no cycles of even length if it is bipartite C) A graph G is 2-colorable if is bipartite D) A graph G can be colored with d+1 colors if d is the maximum degree of any vertex in the graph G E) A graph G can be colored with O(log|v|) colors if it has O(|v|) edges. Choose the correct answer from the options given below:

A	(C) and (E) are incorrect
B	(B) and (C) are incorrect
C	(B) and (E) are incorrect
D	(A) and (D) are incorrect

Data-StructuresGraphs-and-TreeUGC NET JRF November 2020 Paper-2

Question 5 Explanation:

→ Bipartite graph: A graph is bipartite iff the vertices can be partitioned into two sets such that there is no edge between any pair of vertices in the same set.
→ An even cycle graph is always 2-colourable while an odd cycle graph is 3-colourable.
→ A cycle of odd length has chromatic number 3. The chromatic number of any graph must be at least as big as the chromatic number of any of its sub-graphs, so a graph containing an odd cycle can’t be bipartite.
→ Let G be a 2-colorable graph, which means we can color every vertex either red or blue, and no edge will have both endpoints colored the same color. Let A denote the subset of vertices colored red, and let B denote the subset of vertices colored blue. Since all vertices of A are red, there are no edges within A, and similarly for B. This implies that every edge has one endpoint in A and the other in B, which means G is bipartite.
→ Statement E is false because If a graph G has O(√|V|) edges, then we can color G with O(√|V|) colors.

Question 6

Let G be a directed graph whose vertex set is the set of numbers from 1 to 100. There is an edge from a vertex i to a vertex j if and only if either j=i+1 or j=3i. The minimum number of edges in a path in G from vertex 1 to vertex 100 is _______.

A	23
B	99
C	4
D	7

Data-StructuresGraphs-and-TreeUGC NET JRF November 2020 Paper-2

Question 6 Explanation:

Edge set consists of edges from i to j, using either
j = i +1
(or)
j = 3i
Second option will help us reach from 1 to 100 rapidly. The trick to solve this question is to think in the reverse way. Instead of finding a path from 1 to 100, try to find a path from 100 to 1.
So, the edge sequence with minimum number of edges is
1 → 3 → 9 → 10 → 11 → 33 → 99 → 100
which consists of 7 edges.

Question 7

Which of the following is not true for tree and graph?

A	A tree is a graph
B	A graph is a tree
C	Tree can have a cycle
D	Tree is a DAG

Data-StructuresGraphs-and-TreeNIC-NIELIT STA 2020Video-Explanation

Question 7 Explanation:

All are correct except Tree can have a cycle

There are 7 questions to complete.

Access quiz wise question and answers by becoming as a solutions adda PRO SUBSCRIBER with Ad-Free content

If you have registered and made your payment please contact solutionsadda.in@gmail.com to get access