Greedy-approach
Question 1 |
An independent set in a graph is a subset of vertices such that no two vertices in the subset are connected by an edge. An incomplete scheme for a greedy algorithm to find a maximum independent set in a tree is given below:
V: Set of all vertices in the tree; I:=φ;
While V ≠ φdo
begin
select a vertex u; ∈ V such that
V:= V – {u};
if u is such that
then 1:= I ∪ {u}
end;
output(I);
(a) Complete the algorithm by specifying the property of vertex u in each case
(b) What is the time complexity of the algorithm.
Theory Explanation. |
Question 2 |
Consider the undirected graph below:
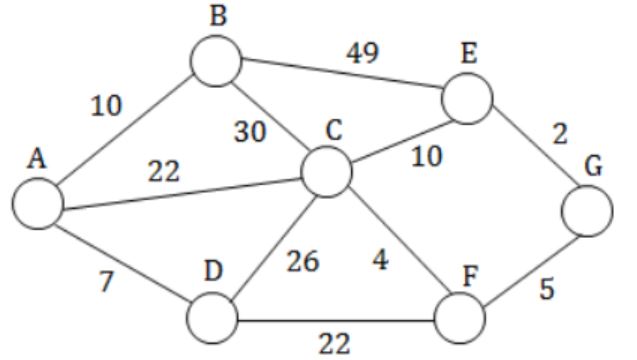
Using Prim's algorithm to construct a minimum spanning tree starting with node A, which one of the following sequences of edges represents a possible order in which the edges would be added to construct the minimum spanning tree?
(E, G), (C, F), (F, G), (A, D), (A, B), (A, C) | |
(A, D), (A, B), (A, C), (C, F), (G, E), (F, G) | |
(A, B), (A, D), (D, F), (F, G), (G, E), (F, C) | |
(A, D), (A, B), (D, F), (F, C), (F, G), (G, E)
|
Question 2 Explanation:
(A) and (B) produce disconnected components with the given order in options which is never allowed by Prim's algorithm.
(C) produces connected component every instead a new edge is added but when first vertex is chosen (first vertex is chosen randomly) first edge must be minimum weight edge that is chosen. Therefore, (A, D) must be chosen before (A, B). Therefore (C) is false.
(C) produces connected component every instead a new edge is added but when first vertex is chosen (first vertex is chosen randomly) first edge must be minimum weight edge that is chosen. Therefore, (A, D) must be chosen before (A, B). Therefore (C) is false.
Question 3 |
Which of the following problem cannot be solved using greedy approach?
0-1 knapsack | |
Job scheduling | |
Minimum spanning tree | |
Huffman code |
Question 3 Explanation:
Greedy Problems:
1. Job scheduling
2. Minimum spanning tree
3. Huffman code
Dynamic Programming:
1. O/1 knapsack
2. Optimal Binary search tree
3. Matrix chain multiplication
1. Job scheduling
2. Minimum spanning tree
3. Huffman code
Dynamic Programming:
1. O/1 knapsack
2. Optimal Binary search tree
3. Matrix chain multiplication
Question 4 |
Consider the following Adjacency matrix corresonding to some weighted Graph ‘G’.
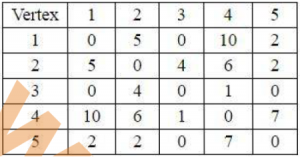
What is the weight of the minimum spanning tree for the graph ‘G’?
11 | |
9 | |
10 | |
8 |
Question 4 Explanation:

Question 5 |
Consider the characters and their frequency counts given in the following table.

Using the Huffman coding technique, which of the following is the valid code for character ‘c’?

Using the Huffman coding technique, which of the following is the valid code for character ‘c’?
11111 | |
1110 | |
11110 | |
110 |
Question 5 Explanation:
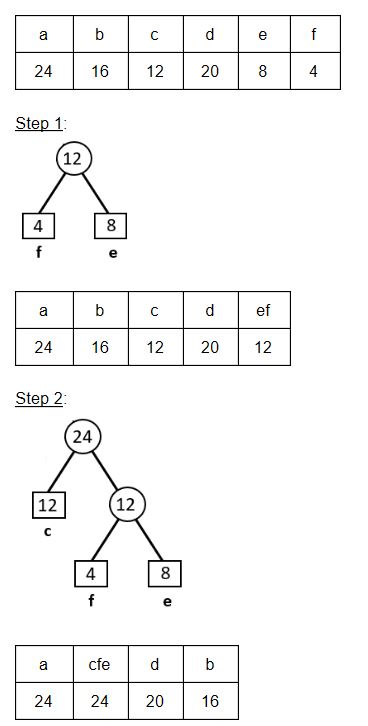
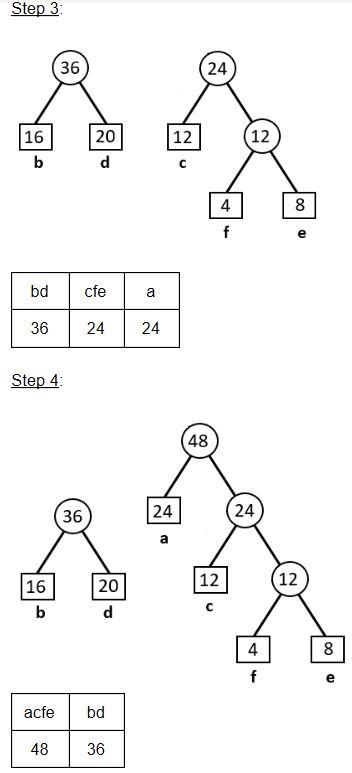

Question 6 |
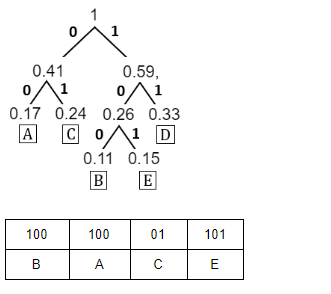
Huffman tree is constructed for the following data: { A, B, C, D, E} with frequency {0.17, 0.11, 0.24, 0.33 and 0.15} respectively. 100 00 01 101 is decoded as
BACE | |
CAD | |
BAD | |
CADD |
Question 6 Explanation:

Question 7 |
Which of the following algorithms is fastest to find shortest path from a source node to a destination node in an un-weighted connected graph?
Warshall’s algorithm | |
Floyd’s algorithm | |
Breadth First Traversal | |
Depth First Traversal |
Question 7 Explanation:
warshall algorithm will take O(n^3) time.
Floyd’s algorithm will take O(n^3) time.
Breadth First traversal will take O(m+n) time.
Depth first traversal will work only if the graph is tree.
Hence among the given options Breadth first traversal is best.
Floyd’s algorithm will take O(n^3) time.
Breadth First traversal will take O(m+n) time.
Depth first traversal will work only if the graph is tree.
Hence among the given options Breadth first traversal is best.
Question 8 |
Which of the following statement is false about Prim's algorithm?
Initially the roots key and nodes are initialized to zero
| |
It may use binomial max heap to represent the primary queue
| |
The complexity is O(E log V) using binary heap
| |
The time complexity is O(E + V log V) using Fibonacci Heap
|
Question 8 Explanation:
S1 is false because only the root key is initialized to zero so that it can be picked first and the rest nodes are initialized to infinity.
The time complexity of Prim's algorithm using binary heap is O( E log V).
And the time complexity of prim's algorithm using Fibonacci heap is O(E + V log V) because the decrease key operation takes O(1) time in Fibonacci heap whereas using binary heap it takes O(log n) time.
The time complexity of Prim's algorithm using binary heap is O( E log V).
And the time complexity of prim's algorithm using Fibonacci heap is O(E + V log V) because the decrease key operation takes O(1) time in Fibonacci heap whereas using binary heap it takes O(log n) time.
There are 8 questions to complete.
