Hashing
Question 1 |
Consider a double hashing scheme in which the primary hash function is h1(k) = k mod 23, and the secondary hash function is h2(k) = 1 + (k mod 19). Assume that the table size is 23. Then the address returned by probe 1 in the probe sequence (assume that the probe sequence begins at probe 0) for key value k=90 is _______.
13 |
• K=90
• h1(k) = k mod 23 = 90 mod 23 = 21
• In case of collision, we need to use secondary hash function.
• h2(k) = 1 + (k mod19) = 1 + 90mod19 = 1+14 = 15
• Now (21+15) mod 23 = 36 mod 23 = 13
• So the address is 13.
Question 2 |
An advantage of chained hash table (external hashing) over the open addressing scheme is
Worst case complexity of search operations is less? | |
Space used is less | |
Deletion is easier | |
None of the above |
Question 3 |
Insert the characters of the string K R P C S N Y T J M into a hash table of size 10.
Use the hash function
h(x) = (ord(x) – ord("a") + 1) mod10
and linear probing to resolve collisions.
(a) Which insertions cause collisions?
(b) Display the final hash table.
Theory Explanation. |
Question 4 |
Given the following input (4322, 1334, 1471, 9679, 1989, 6171, 6173, 4199) and the hash function x mod 10, which of the following statements are true?
-
i) 9679, 1989, 4199 hash to the same value
ii) 1471, 6171 hash to the same value
iii) All elements hash to the same value
iv) Each element hashes to a different value
i only | |
ii only | |
i and ii only | |
iii or iv |
Hash function = x mod 10
Hash values = (2, 4, 1, 9, 9, 1, 3, 9)
9679, 1989, 4199 have same hash values
&
1471, 6171 have same hash values.
Question 5 |
m/n | |
n/m | |
2n/m | |
n/2m |
How?
For 1st element the probability of key1 ends up in slot 1 is 1/m.
For 2nd element the probability of key2 ends up in slot 2 is 1/m
..
..
For nth element the probability of keyn ends up in slot n is 1/m
Hence expected number of elements in a slot is:
1/m+1/m+... (n times)= n/m
In the given question h1 is for elements at even sequence position and h2 is for odd number of sequence positions. This will not affect the overall probability.
Hence here also it is n/m
Question 6 |
- There is a main hash table of size 4.
- The 2 least significant bits of a key is used to index into the main hash table.
- Initially, the main hash table entries are empty.
- Thereafter, when more keys are hashed into it, to resolve collisions, the set of all keys corresponding to a main hash table entry is organized as a binary tree that grows on demand.
- First, the 3rd least significant bit is used to divide the keys into left and right subtrees.
- To resolve more collisions, each node of the binary tree is further sub-divided into left and right subtrees based on the 4th least significant bit.
- A split is done only if it is needed, i.e., only when there is a collison.
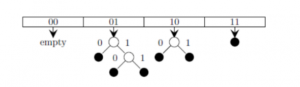
Which of the following sequences of key insertions can cause the above state of the hash table (assume the keys are in decimal notation)?
10, 9, 6, 7, 5, 13 | |
9, 5, 13, 6, 10, 14 | |
9, 5, 10, 6, 7, 1 | |
5, 9, 4, 13, 10, 7 |
The keys are inserted into the main hash table based on their 2 least significant bits.
→ The keys 5, 9, 13 will be inserted in the table with entry “01”.
→ The keys 6 and 10 will be inserted in the table with entry “10”
→ The keys 7 will be inserted in the table with entry “11”
→ Now the entry index 01 has collisions. Check the 3rd least significant bit of the keys 9,5,13. The 3rd least significant bit of the key is 0. Hence, key “9” placed as the left child of “01”. There will be collisions again in between the keys 5 and 13 which need to splitted.
Now check the 4th least significant bit of keys 5 and 13. The key 5 is placed as a left child because the 4th least significant is “0” and the key “13” is placed as right child because its 4th least significant is 1.
→ Now the entry index 10 has a collision. Check the 3rd least significant bit of the keys 10 and 6. The 3rd last significant bit of the key is 0. Hence, “10” is placed as the left child of index “10”.
The 3rd least significant value of “6” is 1. So, we are placed as the right child of index ”10”.
Question 7 |
Consider a hash table of size 11 that uses open addressing with linear probing. Let h(k) = k mod 11 be the hash function used. A sequence of records with keys
43 36 92 87 11 4 71 13 14is inserted into an initially empty hash table, the bins of which are indexed from zero to ten. What is the index of the bin into which the last record is inserted?
2 | |
4 | |
6 | |
7 |
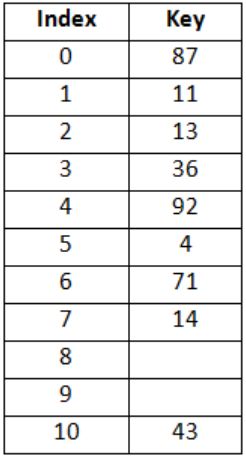
Hence, correct option is (D).
Question 8 |
A hash table with ten buckets with one slot per bucket is shown in the following figure. The symbols S1 to S7 initially entered using a hashing function with linear probing. The maximum number of comparisons needed in searching an item that is not present is
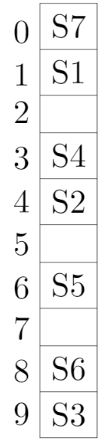
4 | |
5 | |
6 | |
3 |
→ Worst case of finding a number is equal to maximum size of cluster + 1(after searching all the cluster it enters into empty cluster)
→ Maximum no. of comparisons = 4 + 1 = 5
Question 9 |
Division method, i.e., use the hash function h(k) = k mod m. | |
Multiplication method, i.e., use the hash function h(k) = ⌊m(kA − ⌊kA⌋)⌋, where A is a carefully chosen constant. | |
Universal hashing method. | |
If k is a prime number, use Division method. Otherwise, use Multiplication method. |
Question 10 |
Which one of the following hash functions on integers will distribute keys most uniformly over 10 buckets numbered 0 to 9 for i ranging from 0 to 2020?
h(i) = i2 mod 10 | |
h(i) = i3 mod 10 | |
h(i) = (11 *i2) mod 10 | |
h(i) = (12 * i) mod 10 |
Question 11 |
Given a hash table T with 25 slots that stores 2000 elements, the load factor α for T is ___________.
80 | |
70 | |
60 | |
50 |
Question 12 |
A hash table of length 10 uses open addressing with hash function h(k)=k mod 10, and linear probing. After inserting 6 values into an empty hash table, the table is as shown below.
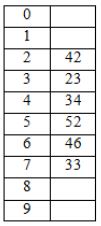
How many different insertion sequences of the key values using the same hash function and linear probing will result in the hash table shown above?
46, 42, 34, 52, 23, 33 | |
34, 42, 23, 52, 33, 46
| |
46, 34, 42, 23, 52, 33 | |
42, 46, 33, 23, 34, 52
|
After inserting 6 values, the table looks like
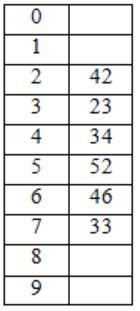
The possible order in which the keys are inserted are:
34, 42, 23, 46 are at their respective slots 4, 2, 3, 6.
52, 33 are at different positions.
― 52 has come after 42, 23, 34 because, it has the collision with 42, because of linear probing, it should have occupy the next empty slot. So 52 is after 42, 23, 34.
― 33 is after 46, because it has the clash with 23. So it got placed in next empty slot 7, which means 2, 3, 4, 5, 6 are filled.
42, 23, 34 may occur in any order but before 52 & 46 may come anywhere but before 33.
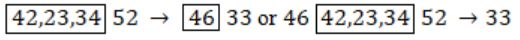
So option (C)

Question 13 |
A hash table of length 10 uses open addressing with hash function h(k)=k mod 10, and linear probing. After inserting 6 values into an empty hash table, the table is as shown below.

How many different insertion sequences of the key values using the same hash function and linear probing will result in the hash table shown above?
10 | |
20 | |
30 | |
40 |
― 33 must be inserted at last (only one possibility)
― 46 can be inserted in any of the 5 places remaining. So 5 ways.
― 52 must be inserted only after inserting 42, 23, 34. So only one choice for 52.
〈42,23,34〉 can be sequenced in 3! ways.
Hence, 5×3! = 30 ways
Question 14 |
Consider a hash table of size seven, with starting index zero, and a hash function (3x + 4) mod 7. Assuming the hash table is initially empty, which of the following is the contents of the table when the sequence 1, 3, 8, 10 is inserted into the table using closed hashing? Note that ‘_’ denotes an empty location in the table.
8, _, _, _, _, _, 10 | |
1, 8, 10, _, _, _, 3 | |
1, _, _, _, _, _,3 | |
1, 10, 8, _, _, _, 3 |
Starting index is zero i.e.,
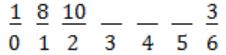
⇾ Given hash function is = (3x+4) mod 3
⇾ Given sequence is = 1, 3, 8, 10
where x = 1 ⟹ (3(1)+4)mod 3 = 0
1 will occupy index 0.
where x = 3 ⟹ (3(3)+4) mod 7 = 6
3 will occupy index 6.
where x = 8 ⟹ (3(8)+4) mod 7 = 0
Index ‘0’ is already occupied then put value(8) at next space (1).
where x = 10 ⟹ (3(10)+4) mod 7 = 6
Index ‘6’ is already occupied then put value(10) at next space (2).
The resultant sequence is (1, 8, 10, __ , __ , __ , 3).
Question 15 |
The keys 12, 18, 13, 2, 3, 23, 5 and 15 are inserted into an initially empty hash table of length 10 using open addressing with hash function h(k) = k mod 10 and linear probing. What is the resultant hash table?
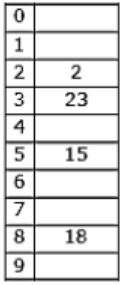 | |
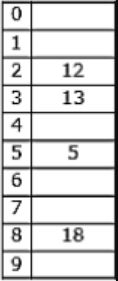 | |
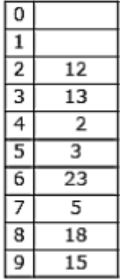 | |
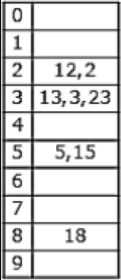 |
They are inserted into an initially empty hash table of length 10 using open addressing with hash function h(k)=k mod 10 & linear probing is used.
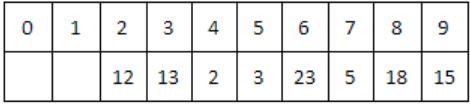
12 % 10 = 2
18 % 10 = 8
13 % 10 = 3
2 % 10 = 2 (Index 4 is empty)
3 % 10 = 3 (Index 5 is empty)
23 % 10 = 3 (Index 6 is empty)
5 % 10 = 5 (Index 7 is empty)
15 % 10 = 5 (Index 9 is empty)
Hence Option C is correct.
A & B doesn’t include all the keys & option D is similar to chaining. So, will go with C.
