Memory-Hierarchy

Question 1

A computer system has a three level memory hierarchy, with access time and hit ratios as shown below:

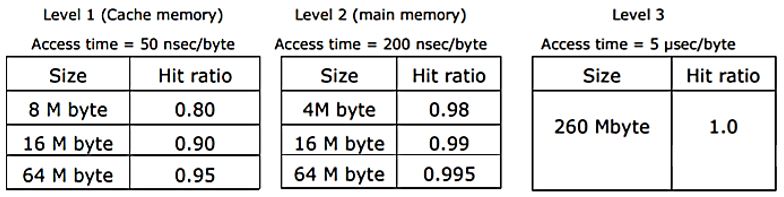
(a) What should be the minimum sizes of level 1 and 2 memories to achieve an average access time of less than 100 nsec?
(b) What is the average access time achieved using the chosen sizes of level 1 and level 2 memories?

A
Theory Explanation.
Computer-OrganizationMemory-HierarchyGATE 1996
Question 2
Let WB and WT be two set associative cache organizations that use LRU algorithm for cache block replacement. WB is a write back cache and WT is a write through cache. Which of the following statements is/are FALSE?
A
Each cache block in WB and WT has a dirty bit.
B
Every write hit in WB leads to a data transfer from cache to main memory.
C
Eviction of a block from WT will not lead to data transfer from cache to main memory
D
A read miss in WB will never lead to eviction of a dirty block from WB.
Computer-OrganizationMemory-HierarchyGATE 2022Video-Explanation
Question 2 Explanation: 
Option A: The given statement is false as cache blocks in WT will not have a dirty bit. Only the cache blocks in WB will have dirty bits associated with them.
Option B: Every write hit in WB need not lead to data transfer from cache to main memory, rather only when that particular block is being evicted there will be transfer from cache to main memory. There can be several write hits in WB before the block is evicted and all those writes will be propagated to the main memory at once. Hence the given statement is false.
Option C: The given statement is true because in WT the writes happen in parallel both in cache and main memory so at the eviction of a block in WT it will not lead to data transfer from cache to main memory.
Option D: A read miss in WB will fetch a new block from main memory and can lead to eviction of a dirty block. Hence the given statement is false.
Question 3

A computer system has an L1 cache, an L2 cache, and a main memory unit connected as shown below. The block size in L1 cache is 4 words. The block size in L2 cache is 16 words. The memory access times are 2 nanoseconds. 20 nanoseconds and 200 nanoseconds for L1 cache, L2 cache and main memory unit respectively.

When there is a miss in L1 cache and a hit in L2 cache, a block is transferred from L2 cache to L1 cache. What is the time taken for this transfer?

A
2 nanoseconds
B
20 nanoseconds
C
22 nanoseconds
D
88 nanoseconds
Computer-OrganizationMemory-HierarchyGATE 2010
Question 3 Explanation: 
Between L1 cache block is of size 4 words, and the bus width between L1 and L2 is also of size 4 words. So only one time the data needs to be transferred from L2 to L1.
And it requires one access of L1 cache and one access of L2 cache. So time taken = 20+2 = 22ns
There are 3 questions to complete.

Access quiz wise question and answers by becoming as a solutions adda PRO SUBSCRIBER with Ad-Free content

If you have registered and made your payment please contact solutionsadda.in@gmail.com to get access