Prepositional-Logic
Question 1 |
Consider the first-order logic sentence F: ∀x(∃yR(x,y)). Assuming non-empty logical domains, which of the sentences below are implied by F?
I. ∃y(∃xR(x,y))
II. ∃y(∀xR(x,y))
III. ∀y(∃xR(x,y))
IV. ¬∃x(∀y¬R(x,y))
I. ∃y(∃xR(x,y))
II. ∃y(∀xR(x,y))
III. ∀y(∃xR(x,y))
IV. ¬∃x(∀y¬R(x,y))
IV only | |
I and IV only | |
II only | |
II and III only |
Question 1 Explanation:
Lets convert the given first order logic sentence into some english sentence.
F: ∀x(∃yR(x,y)) (given)
: For all girls there exist a boyfriend
(x for girls and y for boys)
I: ∃y(∃xR(x,y))
: There exist some boys who have girlfriends.
(Subset of statement F, so True)
II: ∃y(∀xR(x,y))
: There exists some boys for which all the girls are girlfriend. (False)
III: ∀y(∃xR(x,y))
: For all boys exists a girlfriend. (False)
IV: ~∃x(∀y~R(x,y))
= ∀x(~∀y~R(x,y))
= ∀x(∃yR(x,y)) (∵ ~∀y=∃y, ~∃x=∀x)
(True)
F: ∀x(∃yR(x,y)) (given)
: For all girls there exist a boyfriend
(x for girls and y for boys)
I: ∃y(∃xR(x,y))
: There exist some boys who have girlfriends.
(Subset of statement F, so True)
II: ∃y(∀xR(x,y))
: There exists some boys for which all the girls are girlfriend. (False)
III: ∀y(∃xR(x,y))
: For all boys exists a girlfriend. (False)
IV: ~∃x(∀y~R(x,y))
= ∀x(~∀y~R(x,y))
= ∀x(∃yR(x,y)) (∵ ~∀y=∃y, ~∃x=∀x)
(True)
Question 2 |
Let p, q and r be prepositions and the expression (p → q) → r be a contradiction. Then, the expression (r → p) → q is
a tautology | |
a contradiction | |
always TRUE when p is FALSE | |
always TRUE when q is TRUE |
Question 2 Explanation:
Given that (p→q)→r is a contradiction.
So r = F and (p→q) = T.
We have to evaluate the expression
(r→p)→q
Since r = F, (r→p) = T (As F→p, is always true)
The final expression is T→q and this is true when q is true, hence option D.
So r = F and (p→q) = T.
We have to evaluate the expression
(r→p)→q
Since r = F, (r→p) = T (As F→p, is always true)
The final expression is T→q and this is true when q is true, hence option D.
Question 3 |
Let p, q, r denote the statements “It is raining”, “It is cold”, and “It is pleasant”, respectively. Then the statement “It is not raining and it is pleasant, and it is not pleasant only if it is raining and it is cold” is represented by
(¬p ∧ r) ∧ (¬r → (p ∧ q)) | |
(¬p ∧ r) ∧ ((p ∧ q) → ¬r) | |
(¬p ∧ r) ∨ ((p ∧ q) → ¬r) | |
(¬p ∧ r) ∨ (r → (p ∧ q)) |
Question 3 Explanation:
p: It is raining
q: It is cold
r: It is pleasant
“If it is not raining and it is pleasant, and it is not pleasant only if it is raining and it is cold.”
We can divide the statement into two parts with “Conjunction”.
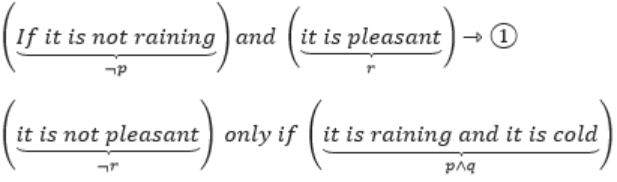
i.e., ¬r→(p∧q) ⇾(2)
From (1) & (2), the given statement can be represented as
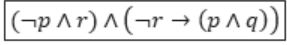
q: It is cold
r: It is pleasant
“If it is not raining and it is pleasant, and it is not pleasant only if it is raining and it is cold.”
We can divide the statement into two parts with “Conjunction”.
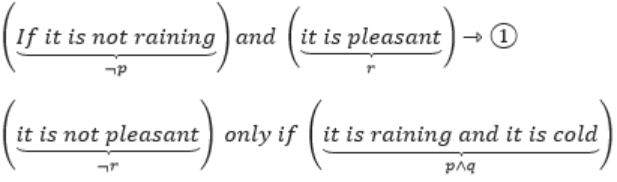
i.e., ¬r→(p∧q) ⇾(2)
From (1) & (2), the given statement can be represented as
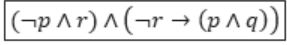
Question 4 |
Let p,q,r,s represent the following propositions.
p: x ∈ {8,9,10,11,12}
q: x is a composite number
r: x is a perfect square<
s: x is a prime number
The integer x≥2 which satisfies ¬((p ⇒ q) ∧ (¬r ∨ ¬s)) is _________.
p: x ∈ {8,9,10,11,12}
q: x is a composite number
r: x is a perfect square<
s: x is a prime number
The integer x≥2 which satisfies ¬((p ⇒ q) ∧ (¬r ∨ ¬s)) is _________.
11 | |
12 | |
13 | |
14 |
Question 4 Explanation:
Given,
~((p→q) ∧ (~r ∨ ~S))
⇒ first simplify the given statement by converging them to ∧, ∨
⇒ [~(p→q) ∨ (~(~r ∨ ~s)]
Demorgan’s law:
⇒ [~(~p ∨ q) ∨ (r ∧ s)]
∵ p→q ≡ ~p ∨ q
⇒ [(p ∧ ~q) ∨ (r ∧ s)]
p ∧ ~q is {8,9,10,11,12} ∧ {not a composite number} i.e. {11}
r ∧ s is {perfect square} ∧ {prime} i.e. no answer
So, the one and only answer is 11.
~((p→q) ∧ (~r ∨ ~S))
⇒ first simplify the given statement by converging them to ∧, ∨
⇒ [~(p→q) ∨ (~(~r ∨ ~s)]
Demorgan’s law:
⇒ [~(~p ∨ q) ∨ (r ∧ s)]
∵ p→q ≡ ~p ∨ q
⇒ [(p ∧ ~q) ∨ (r ∧ s)]
p ∧ ~q is {8,9,10,11,12} ∧ {not a composite number} i.e. {11}
r ∧ s is {perfect square} ∧ {prime} i.e. no answer
So, the one and only answer is 11.
Question 5 |
Consider the following statements:
-
S1: If a candidate is known to be corrupt, then he will not be elected.
S2: If a candidate is kind, he will be elected.
Which one of the following statements follows from S1 and S2 as per sound inference rules of logic?
If a person is known to corrupt, he is kind | |
If a person is not known to be corrupt, he is not kind
| |
If a person is kind, he is not known to be corrupt
| |
If a person is not kind, he is not known to be corrupt |
Question 5 Explanation:
Let p: candidate known to be corrupt
q: candidate will be elected
r: candidate is kind
then S1 = p→~q
= q→~p (conrapositive rule)
and S2: r→q ⇒ r→~p (transitive rule)
i.e., If a person is kind, he is not known to be corrupt. ∴ Option is C
q: candidate will be elected
r: candidate is kind
then S1 = p→~q
= q→~p (conrapositive rule)
and S2: r→q ⇒ r→~p (transitive rule)
i.e., If a person is kind, he is not known to be corrupt. ∴ Option is C
Question 6 |
The CORRECT formula for the sentence, “not all rainy days are cold” is
∀d (Rainy(d) ∧∼Cold(d)) | |
∀d (∼Rainy(d) → Cold(d)) | |
∃d (∼Rainy(d) → Cold(d)) | |
∃d (Rainy(d) ∧∼Cold(d)) |
Question 6 Explanation:
Not all rainy days are cold
= ∼[∀rainy days are cold]
= ∼[∀ days (rainy days ⇒ cold days]
= ∃ days[∼(cold days ∨ ∼rainy days)]
= ∃ days[rainy days ∧ ∼cold days]
= ∼[∀rainy days are cold]
= ∼[∀ days (rainy days ⇒ cold days]
= ∃ days[∼(cold days ∨ ∼rainy days)]
= ∃ days[rainy days ∧ ∼cold days]
There are 6 questions to complete.
