Trees
Question 1 |
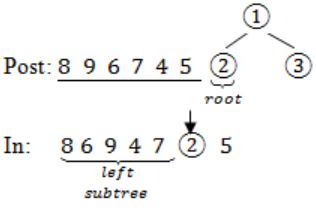
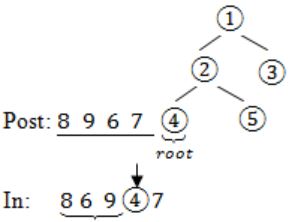
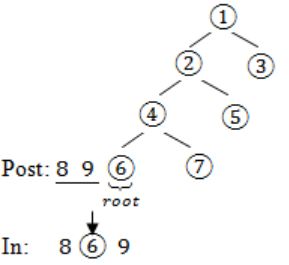
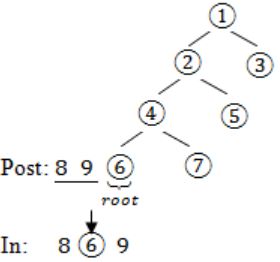
The postorder traversal of a binary tree is 8, 9, 6, 7, 4, 5, 2, 3, 1. The inorder traversal of the same tree is 8, 6, 9, 4, 7, 2, 5, 1, 3. The height of a tree is the length of the longest path from the root to any leaf. The height of the binary tree above is _______.
1 | |
2 | |
3 | |
4 |
In – 8 6 9 4 7 2 5 1 3
Post: 8 9 6 7 4 5 2 3 1→(root)
In: 8 6 9 4 7 2 5→(left subtree) 13→(right subtree)
Question 2 |
The number of leaf nodes in a rooted tree of n nodes, with each node having 0 or 3 children is:
n/2 | |
(n-1)/3 | |
(n-1)/2 | |
(2n+1)/3 |
Question 3 |
A weight-balanced tree is a binary tree in which for each node, the number of nodes in the left subtree is at least half and at most twice the number of nodes in the right subtree. The maximum possible height (number of nodes on the path from the root to the furthest leaf) of such a tree on n nodes is best described by which of the following?
log2n | |
log4/3n | |
log3n | |
log3/2n |
No. of nodes in left sub tree = 2 right sub tree
No. of nodes in left sub tree = (n-1/3)
No. of nodes in right sub tree = 2(n-1/3)

Height of the tree = log3/2 n
Question 4 |
A data structure is required for storing a set of integers such that each of the following operations can be done in O(log n) time, where n is the number of elements in the set.
- I. Deletion of the smallest element
II. Insertion of an element if it is not already present in the set
Which of the following data structures can be used for this purpose?
A heap can be used but not a balanced binary search tree | |
A balanced binary search tree can be used but not a heap | |
Both balanced binary search tree and heap can be used | |
Neither balanced binary search tree nor heap can be used |
Insertion of an element takes O(n).
→ In balanced primary tree deletion takes O(log n).
Insertion also takes O(log n).
Question 5 |
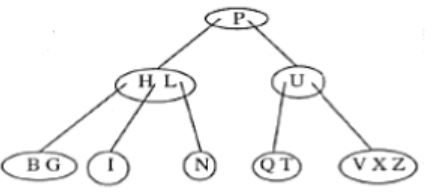
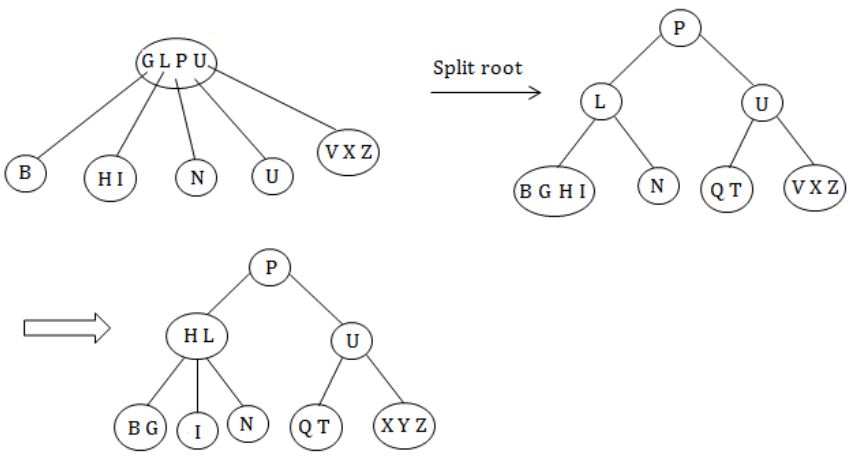
Consider the following 2-3-4 tree (i.e., B-tree with a minimum degree of two) in which each data item is a letter. The usual alphabetical ordering of letters is used in constructing the tree.

What is the result of inserting G in the above tree?
 | |
 | |
 | |
None of the above |
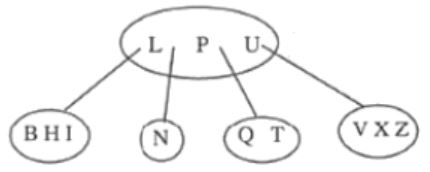
Insert G at root level:
Question 6 |
A 2-3 tree is tree such that
- (a) all internal nodes have either 2 or 3 children
(b) all paths from root to the leaves have the same length
The number of internal nodes of a 2-3 tree having 9 leaves could be
4 | |
5 | |
6 | |
7 | |
Both A and D |
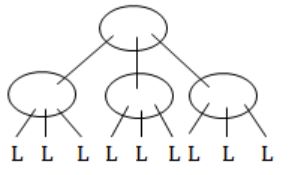
Where L is leaf node.
So, no. of internal node is 4.
Case 2:

Where L is leaf node.
So, no. of internal node is 7.
Question 7 |
If all the edge weights of an undirected graph are positive, then any subset of edges that connects all the vertices and has minimum total weight is a
Hamiltonian cycle | |
grid | |
hypercube | |
tree |
If all edge weights of an undirected graph are positive, then any subset of edges that connects all the vertices and has minimum total weight is minimum spanning tree.
Question 8 |
The height of a tree is the length of the longest root-to-leaf path in it. The maximum and minimum number of nodes in a binary tree of height 5 are
63 and 6, respectively | |
64 and 5, respectively | |
32 and 6, respectively | |
31 and 5, respectively |
2h+1 - 1 = 25+1 - 1 = 63
Minimum number of nodes in a binary tree of height h is
h + 1 = 5 + 1 = 6
Question 9 |
The number of ways in which the numbers 1, 2, 3, 4, 5, 6, 7 can be inserted in an empty binary search tree, such that the resulting tree has height 6, is _________.
Note: The height of a tree with a single node is 0.64 | |
65 | |
66 | |
67 |
So to get such tree at each level we should have either maximum or minimum element from remaining numbers till that level. So no. of binary search tree possible is,
1st level - 2 (maximum or minimum)
⇓
2nd level - 2
⇓
3rd level - 2
⇓
4th level - 2
⇓
5th level - 2
⇓
6th level - 2
⇓
7th level - 2
= 2 × 2 × 2 × 2 × 2 × 2 × 1
= 26
= 64
