Graphs

Question 4

Let G = (V,E) be a directed graph with n vertices. A path from v_i to v_j in G is sequence of vertices (v_i, v_i+1, ……., v_j) such that (v_k, v_k+1) ∈ E for all k in i through j-1. A simple path is a path in which no vertex appears more than once. Let A be an nxn array initialized as follow.

Consider the following algorithm.

for i = 1 to n
   for j = 1 to n
      for k = 1 to n
         A [j,k] = max (A[j,k] (A[j,i] + A [i,k]);

Which of the following statements is necessarily true for all j and k after terminal of the above algorithm?

A	A[j,k] ≤ n
B	If A[j,j] ≥ n-1, then G has a Hamiltonian cycle
C	If there exists a path from j to k, A[j,k] contains the longest path length from j to k
D	If there exists a path from j to k, every simple path from j to k contains at most A[j,k] edges

Algorithms
GraphsGATE 2003

Question 4 Explanation:

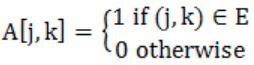
Here, we have two functionalities i.e., from j to k, there exists a path then it results otherwise 0.
If there exist a path then it results
A[j,k] = max(A[j,k], A[j,i]+A[i,k])
i.e., if there exists a path from j to k, every simple path from j to k contains the atmost A[j,k] edges.

Correct Answer: D

Question 4 Explanation:

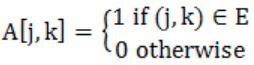
Here, we have two functionalities i.e., from j to k, there exists a path then it results otherwise 0.
If there exist a path then it results
A[j,k] = max(A[j,k], A[j,i]+A[i,k])
i.e., if there exists a path from j to k, every simple path from j to k contains the atmost A[j,k] edges.

UGC NET CS 2014 Dec-Paper-2

Environment

UGC NET CS 2014 Dec-Paper-2

Environment

Graphs

Praveen Singh