Data-Structures
October 8, 2023Computer-Organization
October 8, 2023Data-Structures
|
Question 32
|
Let T be a DFS tree obtained by doing DFS in a connected undirected graph G.
Which of the following options is/are correct?
- Root of T can never be an articulation point in G.
- If u is an articulation point in G such that x is an ancestor of u in T and y is a descendent of u in T, then all paths from x to y in G must pass through u.
- A leaf of T can be an articulation point in G.
- Root of T is an articulation point in G if and only if it has 2 or more children
|
4
|
Statement-2:
Example-1:
If u is an articulation point in G such that x is an ancestor of u in T and y is a descendent of u in T, then all paths from x to y in G must pass through u.
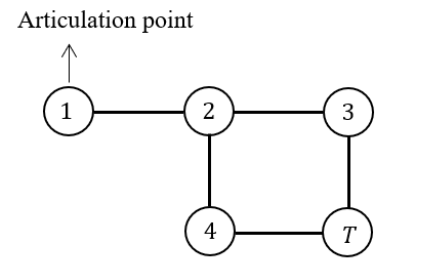
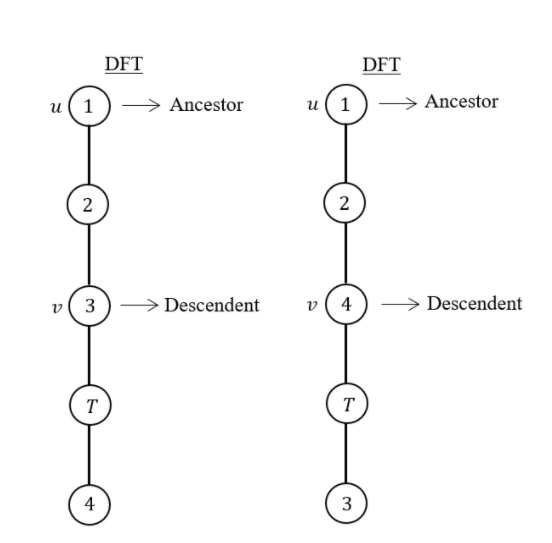

Here 2 and 6 are articulation points.
If you consider node-1 ancestor and node-3 descendent, then without passing through from node -2, there exists a path from one node to another node.
Path from node-1 to node-3
If you consider node-5 ancestor and node-4 descendent, then without passing through from node-6, there exists a path from one node to another node.
Path from node-4 to node-5
The given statement is not TRUE for all cases. So, the given statement is FALSE.
Statement-3: FALSE: Leafs of a DFS-tree are never articulation points.
Statement-4: TRUE: The root of a DFS-tree is an articulation point if and only if it has at least two children.
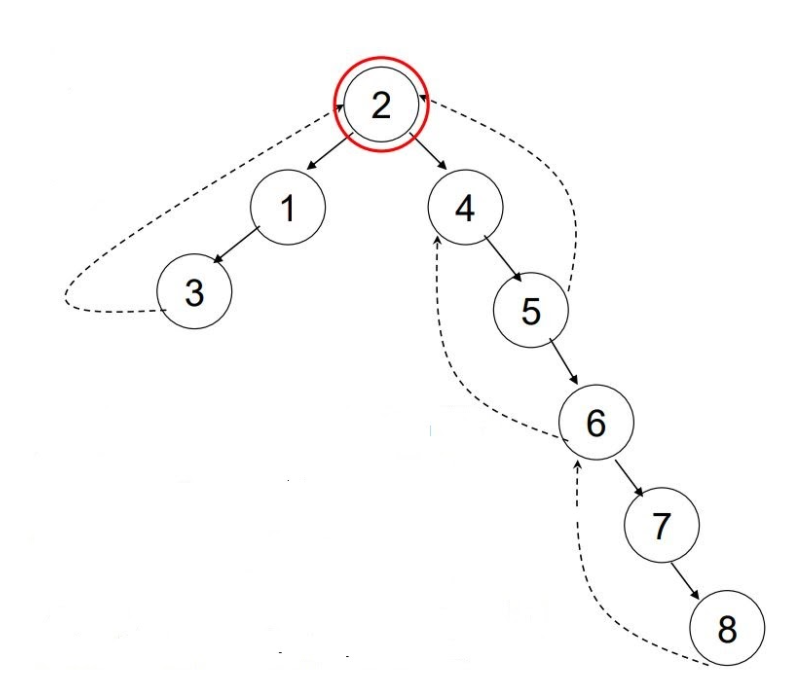
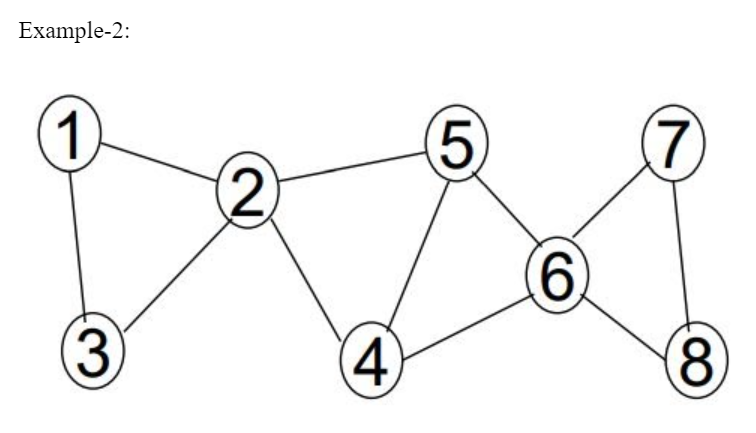
Node 2 is an AP because any node from the first subtree (1, 2) is connected to any node from the second subtree (4, 5, 6, 7, 8) by a path that includes node 2. If node 2 is removed, the 2 subtrees are disconnected.
Statement-2:
Example-1:
If u is an articulation point in G such that x is an ancestor of u in T and y is a descendent of u in T, then all paths from x to y in G must pass through u.




Here 2 and 6 are articulation points.
If you consider node-1 ancestor and node-3 descendent, then without passing through from node -2, there exists a path from one node to another node.
Path from node-1 to node-3
If you consider node-5 ancestor and node-4 descendent, then without passing through from node-6, there exists a path from one node to another node.
Path from node-4 to node-5
The given statement is not TRUE for all cases. So, the given statement is FALSE.
Statement-3: FALSE: Leafs of a DFS-tree are never articulation points.
Statement-4: TRUE: The root of a DFS-tree is an articulation point if and only if it has at least two children.


Node 2 is an AP because any node from the first subtree (1, 2) is connected to any node from the second subtree (4, 5, 6, 7, 8) by a path that includes node 2. If node 2 is removed, the 2 subtrees are disconnected.
