KVS DEC-2013
October 11, 2023Operating-Systems
October 11, 2023Data-Structures
|
Question 30
|
- There is a main hash table of size 4.
- The 2 least significant bits of a key is used to index into the main hash table.
- Initially, the main hash table entries are empty.
- Thereafter, when more keys are hashed into it, to resolve collisions, the set of all keys corresponding to a main hash table entry is organized as a binary tree that grows on demand.
- First, the 3rd least significant bit is used to divide the keys into left and right subtrees.
- To resolve more collisions, each node of the binary tree is further sub-divided into left and right subtrees based on the 4th least significant bit.
- A split is done only if it is needed, i.e., only when there is a collison.
Consider the following state of the hash table.
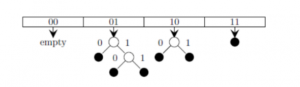
Which of the following sequences of key insertions can cause the above state of the hash table (assume the keys are in decimal notation)?
|
10, 9, 6, 7, 5, 13
|
|
|
9, 5, 13, 6, 10, 14
|
|
|
9, 5, 10, 6, 7, 1
|
|
|
5, 9, 4, 13, 10, 7
|
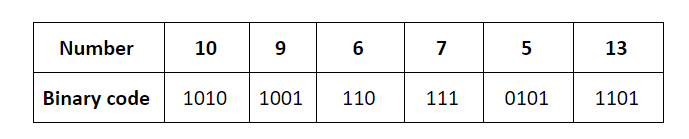
The keys are inserted into the main hash table based on their 2 least significant bits.
→ The keys 5, 9, 13 will be inserted in the table with entry “01”.
→ The keys 6 and 10 will be inserted in the table with entry “10”
→ The keys 7 will be inserted in the table with entry “11”
→ Now the entry index 01 has collisions. Check the 3rd least significant bit of the keys 9,5,13. The 3rd least significant bit of the key is 0. Hence, key “9” placed as the left child of “01”. There will be collisions again in between the keys 5 and 13 which need to splitted.
Now check the 4th least significant bit of keys 5 and 13. The key 5 is placed as a left child because the 4th least significant is “0” and the key “13” is placed as right child because its 4th least significant is 1.
→ Now the entry index 10 has a collision. Check the 3rd least significant bit of the keys 10 and 6. The 3rd last significant bit of the key is 0. Hence, “10” is placed as the left child of index “10”.
The 3rd least significant value of “6” is 1. So, we are placed as the right child of index ”10”.

The keys are inserted into the main hash table based on their 2 least significant bits.
→ The keys 5, 9, 13 will be inserted in the table with entry “01”.
→ The keys 6 and 10 will be inserted in the table with entry “10”
→ The keys 7 will be inserted in the table with entry “11”
→ Now the entry index 01 has collisions. Check the 3rd least significant bit of the keys 9,5,13. The 3rd least significant bit of the key is 0. Hence, key “9” placed as the left child of “01”. There will be collisions again in between the keys 5 and 13 which need to splitted.
Now check the 4th least significant bit of keys 5 and 13. The key 5 is placed as a left child because the 4th least significant is “0” and the key “13” is placed as right child because its 4th least significant is 1.
→ Now the entry index 10 has a collision. Check the 3rd least significant bit of the keys 10 and 6. The 3rd last significant bit of the key is 0. Hence, “10” is placed as the left child of index “10”.
The 3rd least significant value of “6” is 1. So, we are placed as the right child of index ”10”.
