Algorithms
October 12, 2023Hashing
October 12, 2023GATE 2022
| Question 11 |
Which one of the following statements is TRUE for all positive functions f (n) ?
| f ( n ^2 ) ( f ( n ) ^2 ), when f ( n ) is a polynomial | |
| f ( n ^2 ) o ( f ( n ) ^2 ) | |
| f ( n ^2 ) O ( f ( n ) ^2 ), when f ( n ) is an exponential function | |
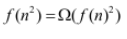 |
Question 11 Explanation:
constant < logarithmic < linear < polynomial < exponential < factorial
f(n)=n^c where c is a constant
f(n^2) = (n^2)^c = n^2c
(f(n))^2 = (n^c)^2 = n^2c
f(n^2) = (f(n))^2 is TRUE asymptotically.
Option-B: FALSE: The small omega function indicates the tightest upper bound.
f(n)^2 < o(f(n)^2) is FALSE asymptotically.
Option-C: FALSE: Consider f(n)=logn
f(n^2)=logn^2 = 2*logn
(f(n))^2 = (logn)^2 = logn * logn
f(n^2) <=Ω(f(n))^2 is FALSE asymptotically.
Option-D: FALSE:
Exponential values(Eg: 2^n, 3^n,..,k^n where k is a constant ”
f(n)=3^n
f(n^2)=f(3^(n^2)
(f(n))^2 = (3^n)^2 = 3^2n
f(n^2) >= O(f(n))^2 is FALSE asymptotically.
f(n)=n^c where c is a constant
f(n^2) = (n^2)^c = n^2c
(f(n))^2 = (n^c)^2 = n^2c
f(n^2) = (f(n))^2 is TRUE asymptotically.
Option-B: FALSE: The small omega function indicates the tightest upper bound.
f(n)^2 < o(f(n)^2) is FALSE asymptotically.
Option-C: FALSE: Consider f(n)=logn
f(n^2)=logn^2 = 2*logn
(f(n))^2 = (logn)^2 = logn * logn
f(n^2) <=Ω(f(n))^2 is FALSE asymptotically.
Option-D: FALSE:
Exponential values(Eg: 2^n, 3^n,..,k^n where k is a constant ”
f(n)=3^n
f(n^2)=f(3^(n^2)
(f(n))^2 = (3^n)^2 = 3^2n
f(n^2) >= O(f(n))^2 is FALSE asymptotically.
Correct Answer: A
Question 11 Explanation:
constant < logarithmic < linear < polynomial < exponential < factorial
f(n)=n^c where c is a constant
f(n^2) = (n^2)^c = n^2c
(f(n))^2 = (n^c)^2 = n^2c
f(n^2) = (f(n))^2 is TRUE asymptotically.
Option-B: FALSE: The small omega function indicates the tightest upper bound.
f(n)^2 < o(f(n)^2) is FALSE asymptotically.
Option-C: FALSE: Consider f(n)=logn
f(n^2)=logn^2 = 2*logn
(f(n))^2 = (logn)^2 = logn * logn
f(n^2) <=Ω(f(n))^2 is FALSE asymptotically.
Option-D: FALSE:
Exponential values(Eg: 2^n, 3^n,..,k^n where k is a constant ”
f(n)=3^n
f(n^2)=f(3^(n^2)
(f(n))^2 = (3^n)^2 = 3^2n
f(n^2) >= O(f(n))^2 is FALSE asymptotically.
f(n)=n^c where c is a constant
f(n^2) = (n^2)^c = n^2c
(f(n))^2 = (n^c)^2 = n^2c
f(n^2) = (f(n))^2 is TRUE asymptotically.
Option-B: FALSE: The small omega function indicates the tightest upper bound.
f(n)^2 < o(f(n)^2) is FALSE asymptotically.
Option-C: FALSE: Consider f(n)=logn
f(n^2)=logn^2 = 2*logn
(f(n))^2 = (logn)^2 = logn * logn
f(n^2) <=Ω(f(n))^2 is FALSE asymptotically.
Option-D: FALSE:
Exponential values(Eg: 2^n, 3^n,..,k^n where k is a constant ”
f(n)=3^n
f(n^2)=f(3^(n^2)
(f(n))^2 = (3^n)^2 = 3^2n
f(n^2) >= O(f(n))^2 is FALSE asymptotically.
