![GATE 2017 [Set-1]](https://solutionsadda.in/wp-content/uploads/2019/05/green-new-logo.png){kind=logo}
Digital-Logic-Design
October 12, 2023GATE 2017 [Set-1]
October 12, 2023GATE 2017 [Set-1]
|
Question 4
|
Consider the following functions from positives integers to real numbers
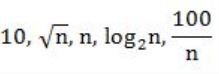
The CORRECT arrangement of the above functions in increasing order of asymptotic complexity is:
 |
|
 |
|
 |
|
 |
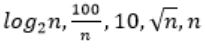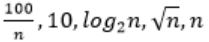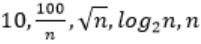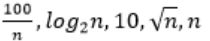Question 4 Explanation:
In this problem, they are expecting to find us “increasing order of asymptotic complexity”.
Step-1: Take n=2048 or 211 (Always take n is very big number)
Step-2: Divide functions into 2 ways
1. Polynomial functions
2. Exponential functions
Step-3: The above functions are belongs to polynomial. So, simply substitute the value of n,
First compare with constant values.
→ 100 / 2048 = 0.048828125
→ 10 > 100/ 2048
→ log2 2048 =11
→ √n = 45.25483399593904156165403917471
→ n = 2048
So, Option B is correct
Step-1: Take n=2048 or 211 (Always take n is very big number)
Step-2: Divide functions into 2 ways
1. Polynomial functions
2. Exponential functions
Step-3: The above functions are belongs to polynomial. So, simply substitute the value of n,
First compare with constant values.
→ 100 / 2048 = 0.048828125
→ 10 > 100/ 2048
→ log2 2048 =11
→ √n = 45.25483399593904156165403917471
→ n = 2048
So, Option B is correct
Correct Answer: B
Question 4 Explanation:
In this problem, they are expecting to find us “increasing order of asymptotic complexity”.
Step-1: Take n=2048 or 211 (Always take n is very big number)
Step-2: Divide functions into 2 ways
1. Polynomial functions
2. Exponential functions
Step-3: The above functions are belongs to polynomial. So, simply substitute the value of n,
First compare with constant values.
→ 100 / 2048 = 0.048828125
→ 10 > 100/ 2048
→ log2 2048 =11
→ √n = 45.25483399593904156165403917471
→ n = 2048
So, Option B is correct
Step-1: Take n=2048 or 211 (Always take n is very big number)
Step-2: Divide functions into 2 ways
1. Polynomial functions
2. Exponential functions
Step-3: The above functions are belongs to polynomial. So, simply substitute the value of n,
First compare with constant values.
→ 100 / 2048 = 0.048828125
→ 10 > 100/ 2048
→ log2 2048 =11
→ √n = 45.25483399593904156165403917471
→ n = 2048
So, Option B is correct
Subscribe
Login
0 Comments