Software-Engineering
October 14, 2023GATE 2017 [Set-1]
October 14, 2023GATE 2007
| Question 1 |
Consider the following two statements about the function f(x)=|x|
P. f(x) is continuous for all real values of x Q. f(x) is differentiable for all real values of x
Which of the following is TRUE?
| P is true and Q is false. | |
| P is false and Q is true. | |
| Both P and Q are true. | |
| Both P and Q are false. |
Question 1 Explanation:
f(x) = |x|
→ f(x) is continuous for all real values of x

For every value of x, there is corresponding value of f(x).
For x is positive, f(x) is also positive
x is negative, f(x) is positive.
So, f(x) is continuous for all real values of x.
→ f(x) is not differentiable for all real values of x.
For x<0, derivative is negative
x>0, derivative is positive.
Here, left derivative and right derivatives are not equal.
→ f(x) is continuous for all real values of x
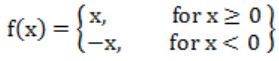
For every value of x, there is corresponding value of f(x).
For x is positive, f(x) is also positive
x is negative, f(x) is positive.
So, f(x) is continuous for all real values of x.
→ f(x) is not differentiable for all real values of x.
For x<0, derivative is negative
x>0, derivative is positive.
Here, left derivative and right derivatives are not equal.
Correct Answer: A
Question 1 Explanation:
f(x) = |x|
→ f(x) is continuous for all real values of x

For every value of x, there is corresponding value of f(x).
For x is positive, f(x) is also positive
x is negative, f(x) is positive.
So, f(x) is continuous for all real values of x.
→ f(x) is not differentiable for all real values of x.
For x<0, derivative is negative
x>0, derivative is positive.
Here, left derivative and right derivatives are not equal.
→ f(x) is continuous for all real values of x
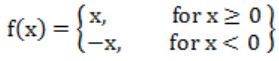
For every value of x, there is corresponding value of f(x).
For x is positive, f(x) is also positive
x is negative, f(x) is positive.
So, f(x) is continuous for all real values of x.
→ f(x) is not differentiable for all real values of x.
For x<0, derivative is negative
x>0, derivative is positive.
Here, left derivative and right derivatives are not equal.
Subscribe
Login
0 Comments
