Question 1457 – Data-Structures
November 28, 2023UGC NET JRF November 2020 Paper-2
November 28, 2023UGC NET JRF November 2020 Paper-2
| Question 6 |
Consider the following languages:
L1={aźZ| ź is an integer}
L2={azź | ź>0}
L3={ωω| ω{a,b}*}
Which of the languages is (are) regular?
L1={aźZ| ź is an integer}
L2={azź | ź>0}
L3={ωω| ω{a,b}*}
Which of the languages is (are) regular?
| L1 and L2 only | |
| L1 and L3 only | |
| L1 only | |
| L2 only | |
| None of the above |
Question 6 Explanation:
A language is Regular language only if it creates an AP series.
Here only statement 2 makes an AP series. Example: L be a lanusage where i=1 and Z>= 0 then L ={ epsilon, a, aa, aaa, aaaa,………………} which is an AP. And Finite automata for this will be

Here only statement 2 makes an AP series. Example: L be a lanusage where i=1 and Z>= 0 then L ={ epsilon, a, aa, aaa, aaaa,………………} which is an AP. And Finite automata for this will be
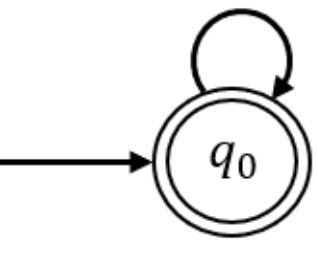
Correct Answer: E
Question 6 Explanation:
A language is Regular language only if it creates an AP series.
Here only statement 2 makes an AP series. Example: L be a lanusage where i=1 and Z>= 0 then L ={ epsilon, a, aa, aaa, aaaa,………………} which is an AP. And Finite automata for this will be

Here only statement 2 makes an AP series. Example: L be a lanusage where i=1 and Z>= 0 then L ={ epsilon, a, aa, aaa, aaaa,………………} which is an AP. And Finite automata for this will be

