Subnetting
December 9, 2023Question 5600 – NIELIT Junior Teachnical Assistant_2016_march
December 9, 2023Theory-of-Computation
| Question 1 |
Consider the language L over the alphabet {0, 1}, given below:
L = {w ε {0, 1}* | w does not contain three or more consecutive 1’s}.
The minimum number of states in a Deterministic Finite-State Automaton (DFA) for L is _____?
L = {w ε {0, 1}* | w does not contain three or more consecutive 1’s}.
The minimum number of states in a Deterministic Finite-State Automaton (DFA) for L is _____?
| 4 |
Question 1 Explanation:
L = {ε, 0, 1, 01…….}
L’ = complement of L = {111,0111,1110,110111001,……..}
It’s easy to visualize L’ rather than L thus the given problem is simply a complement of minimal DFA having 3 consecutive 1’s over the input {0,1}.
We can take complement by simply changing the non-final state to the final state and vice-versa.
The Minimal DFA not containing 3 or more consecutive 1’s will require 4 states out of which 3 are final and 1 is dead state.
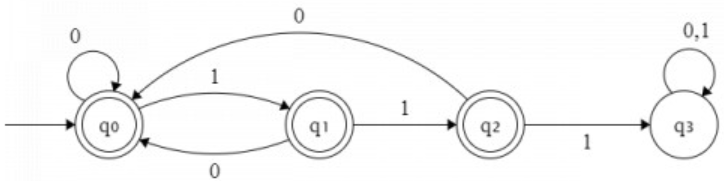
DFA for L is:

L’ = complement of L = {111,0111,1110,110111001,……..}
It’s easy to visualize L’ rather than L thus the given problem is simply a complement of minimal DFA having 3 consecutive 1’s over the input {0,1}.
We can take complement by simply changing the non-final state to the final state and vice-versa.
The Minimal DFA not containing 3 or more consecutive 1’s will require 4 states out of which 3 are final and 1 is dead state.
DFA for L is:
Correct Answer: A
Question 1 Explanation:
L = {ε, 0, 1, 01…….}
L’ = complement of L = {111,0111,1110,110111001,……..}
It’s easy to visualize L’ rather than L thus the given problem is simply a complement of minimal DFA having 3 consecutive 1’s over the input {0,1}.
We can take complement by simply changing the non-final state to the final state and vice-versa.
The Minimal DFA not containing 3 or more consecutive 1’s will require 4 states out of which 3 are final and 1 is dead state.
DFA for L is:

L’ = complement of L = {111,0111,1110,110111001,……..}
It’s easy to visualize L’ rather than L thus the given problem is simply a complement of minimal DFA having 3 consecutive 1’s over the input {0,1}.
We can take complement by simply changing the non-final state to the final state and vice-versa.
The Minimal DFA not containing 3 or more consecutive 1’s will require 4 states out of which 3 are final and 1 is dead state.
DFA for L is:

