GATE 2008
March 14, 2025GATE 2008
March 14, 2025GATE 2008
| Question 13 |
If L and 
are recursively enumerable, then L is
| regular | |
| context-free | |
| context-sensitive | |
| recursive |
Question 13 Explanation:
If L is recursive enumerable, then it implies that there exist a Turing Machine (lets say M1) which always HALT for the strings which is in L.
If
are recursively enumerable, then it implies that there exist a Turing Machine (lets say M2) which always HALT for the strings which is NOT in L(as L is complement of <img src="https://solutionsadda.in/wp-content/uploads/2020/01/g5-5.jpg" ).=""
Since we can combine both Turing machines (M1 and M2) and obtain a new Turing Machine (say M3) which always HALT for the strings if it is in L and also if it is not in L. This implies that L must be recursive.
If
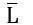are recursively enumerable, then it implies that there exist a Turing Machine (lets say M2) which always HALT for the strings which is NOT in L(as L is complement of <img src="https://solutionsadda.in/wp-content/uploads/2020/01/g5-5.jpg" ).="" Since we can combine both Turing machines (M1 and M2) and obtain a new Turing Machine (say M3) which always HALT for the strings if it is in L and also if it is not in L. This implies that L must be recursive.
Correct Answer: D
Question 13 Explanation:
If L is recursive enumerable, then it implies that there exist a Turing Machine (lets say M1) which always HALT for the strings which is in L.
If are recursively enumerable, then it implies that there exist a Turing Machine (lets say M2) which always HALT for the strings which is NOT in L(as L is complement of <img src="https://solutionsadda.in/wp-content/uploads/2020/01/g5-5.jpg" ).=""
Since we can combine both Turing machines (M1 and M2) and obtain a new Turing Machine (say M3) which always HALT for the strings if it is in L and also if it is not in L. This implies that L must be recursive.
If
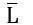are recursively enumerable, then it implies that there exist a Turing Machine (lets say M2) which always HALT for the strings which is NOT in L(as L is complement of <img src="https://solutionsadda.in/wp-content/uploads/2020/01/g5-5.jpg" ).="" Since we can combine both Turing machines (M1 and M2) and obtain a new Turing Machine (say M3) which always HALT for the strings if it is in L and also if it is not in L. This implies that L must be recursive.