UGC NET CS 2014 Dec-Paper-2
October 25, 2023GATE 1994
October 25, 2023GATE 1993
| Question 1 |
The eigen vector(s) of the matrix
is (are)
| (0,0,α ) | |
| (α,0,0) | |
| (0,0,1) | |
| (0,α,0) | |
| Both B and D |
Question 1 Explanation:
Since, the given matrix is an upper triangular one, all eigen values are A. And hence A – λI = A.
So the question as has
(A – λI)X = 0
AX = 0

What x1, x2, x3 are suitable?
Which means:
x1 times column 1 + x2 times column 2 + x3 times column 3 = zero vector
Since α is not equal to zero, so x3 must be necessarily zero to get zero vector.
Hence, only (B) and (D) satisfies.
So the question as has
(A – λI)X = 0
AX = 0
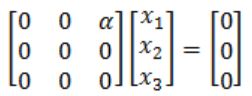
What x1, x2, x3 are suitable?
Which means:
x1 times column 1 + x2 times column 2 + x3 times column 3 = zero vector
Since α is not equal to zero, so x3 must be necessarily zero to get zero vector.
Hence, only (B) and (D) satisfies.
Correct Answer: E
Question 1 Explanation:
Since, the given matrix is an upper triangular one, all eigen values are A. And hence A – λI = A.
So the question as has
(A – λI)X = 0
AX = 0

What x1, x2, x3 are suitable?
Which means:
x1 times column 1 + x2 times column 2 + x3 times column 3 = zero vector
Since α is not equal to zero, so x3 must be necessarily zero to get zero vector.
Hence, only (B) and (D) satisfies.
So the question as has
(A – λI)X = 0
AX = 0
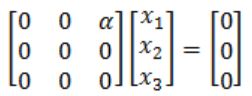
What x1, x2, x3 are suitable?
Which means:
x1 times column 1 + x2 times column 2 + x3 times column 3 = zero vector
Since α is not equal to zero, so x3 must be necessarily zero to get zero vector.
Hence, only (B) and (D) satisfies.
