JT(IT) 2016 PART-B Computer Science
Question 1 |
If a random variable takes a finite set of values it is called:
Continuous variate | |
Normal variate
| |
Discrete variate
| |
Exponential variate |
Examples:
number of students present
number of red marbles in a jar
number of heads when flipping three coins
students’ grade level
→ A discrete random variable X has a countable number of possible values.
Example:
Let X represent the sum of two dice.
→ A discrete random variable is one which may take on only a countable number of distinct values such as 0,1,2,3,4,........ Discrete random variables are usually (but not necessarily) counts. If a random variable can take only a finite number of distinct values, then it must be discrete.
Examples of discrete random variables include the number of children in a family, the Friday night attendance at a cinema, the number of patients in a doctor's surgery, the number of defective light bulbs in a box of ten.
Question 2 |
In client-server computing vertical scaling means:
Adding or removing client workstations with only a slight performance impact
| |
Migrating servers to a new group of client workstations | |
Migrating client workstations to a larger and faster server machine or multi servers | |
Combining two or more client workstation groups
|
→ Vertical Scaling is most commonly used in applications and products of middle-range as well as small and middle-sized companies. One of the most common examples of Virtual Scaling is to buy an expensive hardware and use it as a Virtual Machine hypervisor (VMWare ESX).
→ Vertical Scaling usually means upgrade of server hardware. Some of the reasons to scale vertically includes increasing IOPS (Input / Output Operations), amplifying CPU/RAM capacity, as well as disk capacity.
→ However, even after using virtualization, whenever an improved performance is targeted, the risk for downtimes with it is much higher than using horizontal scaling.
Question 3 |
If the mean of a poisson distribution is m, then standard deviation of the distribution is:
m2 | |
m | |
2*m | |
√m |
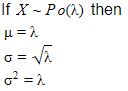
Question 4 |
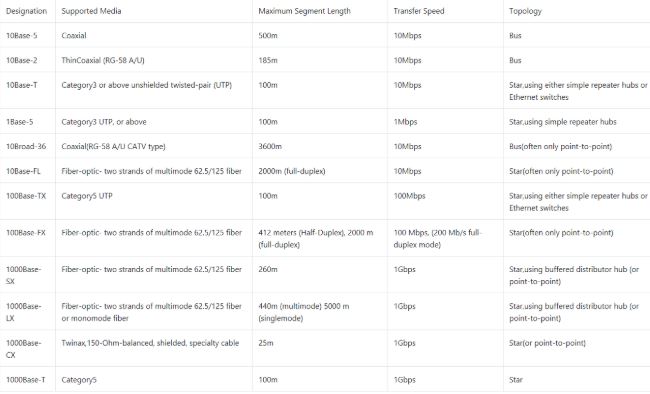
The 10Base5 cabling scheme of ethernet uses:
Twisted pairs
| |
Fiber optics | |
Thin coax
| |
Thick coax |
10Base5 is also called thick Ethernet, ThickWire, and ThickNet.
→ The number 10: At the front of each identifier, 10 denotes the standard data transfer speed over these media - ten megabits per second (10Mbps).
→ The word Base: Short for Baseband, this part of the identifier signifies a type of network that uses only one carrier frequency for signaling and requires all network stations to share its use.
→ The segment type or segment length: This part of the identifier can be a digit or a letter:
- Digit - shorthand for how long (in meters) a cable segment may be before attenuation sets in.
For example, a 10Base5 segment can be no more than 500 meters long.
- Letter - identifies a specific physical type of cable.
For example, the T at the end of 10BaseT stands for twisted-pair.
Question 5 |
The standard deviation of binomial distribution with n observations and probability of success p, probability of failure is q is:
√npq
| |
Pq | |
Np | |
√pq |
The binomial distribution for a random variable X with parameters n and p represents the sum of n independent variables Z which may assume the values 0 or 1. If the probability that each Z variable assumes the value 1 is equal to p, then the mean of each variable is equal to l*p + 0*(l-p) = p, and the variance is equal to p(l-p).
By the addition properties for independent random variables, the mean and variance of the binomial distribution are equal to the sum of the means and variances of the n independent Z variables, so
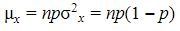
These definitions are intuitively logical. Imagine, for example 8 flips of a coin. If the coin is fair, then p = 0.5. One would expect the mean number of heads to be half the flips, or np = 8*0.5 = 4.
The variance is equal to np(l-p) = 8*0.5*0.5 = 2.
Question 6 |
One of the ad-hoc solutions to count to infinity problem in network routing is:
The split horizon hack
| |
Flow based routing | |
Flooding
| |
Shortest path routing
|
1. Route Poison
2. The split horizon hack
Question 7 |
The normal curve is symmetrical about its:
Standard deviation | |
Mean
| |
Variance | |
Probability
|
The probability density of the normal distribution is

Where
• μ is the mean or expectation of the distribution (and also its median and mode).
• σ is the standard deviation, and
• 2 is the variance
Question 8 |
Given a bit rate of b bits/sec, the time required to send 16 bits is:
16*b sec
| |
16/b sec
| |
16b sec | |
b16 sec
|
The data rate R is a function of the duration of the bit or bit time (TB).
R = 1/TB
Question 9 |
The density of uniform distribution over the interval -⍺ < a < b < ⍺ is given by:
f(x) = λe-λx , x>=0
| |
f(x) = qkp | |
f(x) = 1/(b-a), a | |
f(x) = (⍺/c)x⍺-1 |
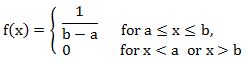
The values of f(x) at the two boundaries a and b are usually unimportant because they do not alter the values of the integrals of f(X) dX over any interval, not of X f(X) dX or any higher moment. Sometimes they are chosen to be zero, and sometimes chosen to be 1/(b – a). The latter is appropriate in the context of estimation by the method of maximum likelihood. In the context of Fourier analysis, one may lake the value of f(a) to be 1|2(b – a), since then the inverse transform of may integral transform of this uniform function will yield back the function itself, rather than a function which equal ‘almost everywhere’, i.e except on a set of points with zero measure. Also, it is consistent with the sign function which has no such ambiguity.
In terms of mean and variance σ2, the probability density may be written as:
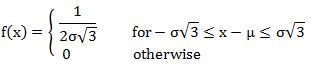
Question 10 |
The built in HTTP request method to request to read a web page is:
HEAD | |
PUT
| |
GET
| |
POST |
The request method indicates the method to be performed on the resource identified by the given Request-URI. The method is case-sensitive and should always be mentioned in uppercase. The following table lists all the supported methods in HTTP/1.1.

Question 11 |
Exponential distribution is special case of ____ distribution.
Theta | |
Alpha | |
Beta | |
Gamma |
Question 12 |
The traditional cryptographic cipher that records the letters but do not disguise them is:
Substitute cipher | |
One-time pads
| |
Secret key algorithms
| |
Transposition cipher |
Also this code can be easily broken.
Question 13 |
0 | |
1 | |
-1 | |
⍺ |
Question 14 |
The segmentation memory management scheme suffers from:
External fragmentation | |
Internal fragmentation
| |
Starvation
| |
Ageing
|
Paging avoids external fragmentation but still it suffers from internal fragmentation. < br> • Internal fragmentation is the wasted space within each allocated block because of rounding up from the actual requested allocation to the allocation granularity.
• External fragmentation is the various free spaced holes that are generated in either your memory or disk space. External fragmented blocks are available for allocation, but may be too small to be of any use.
• Resource starvation is a problem encountered in concurrent computing where a process is perpetually denied necessary resources to process its work. Starvation may be caused by errors in a scheduling or mutual exclusion algorithm.
• Ageing is a scheduling technique used to avoid starvation.
Question 15 |
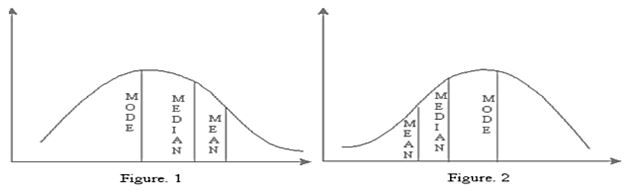
The mean, mode and median are connected by the empirical relationship:
Mean-mode = 2(mean-median)
| |
Mean-mode = 3(mean-median) | |
Mean-mode = (mean-mode)/2
| |
Mean-mode = (mean-mode)/3
|
Mode = mean - 3 [mean - median]
Mode = 3 median - 2 mean
and Median = mode + ⅔ [mean-mode]