Probability
Question 1 |
The probability that a number selected at random between 100 and 999 (both inclusive) will not contain the digit 7 is:
16/25 | |
(9/10)3 | |
27/75 | |
18/25 |
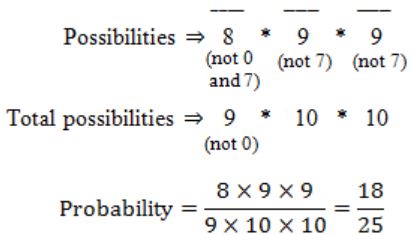
Question 2 |
A bag contains 10 white balls and 15 black balls. Two balls are drawn in succession. The probability that one of them is black and the other is white is:
2/3 | |
4/5 | |
1/2 | |
2/1 |

Probability of first ball black and second one white is,
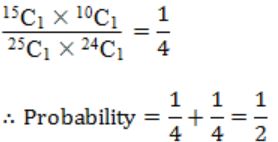
Question 3 |
For n>2, let a ∈ {0,1}n be a non-zero vector. Suppose that x is chosen uniformly at random from {0,1}n. Then, the probability that is an odd number ![]() is _____.
is _____.
0.5 |
‘x’ is a vector chosen randomly from {0,1}n
‘a’ can have 2(n-1) possibilities, x can have 2n possibilities.
∑aixi have (2n-1)(2n) possibilities, which is an even number of outcomes.
The probability of https://solutionsadda.in/wp-content/uploads/2020/02/41.jpg is odd is ½.
For example:
Take n=3
a = {001, 010, 100, 011, 101, 111}
x = {000, 001, 010, 011, 100, 101, 110, 111}
Computed as [001]×[000] = 0+0+0 = 0 Output = even
[001]×[001] = 0+0+1 = 0 Output = odd
Similarly, there could be 28 even, 28 odd outputs for the a(size=7), x(size=8) of total 56 outputs.
Question 4 |
Two dice are thrown simultaneously. The probability that at least one of them will have 6 facing up is
1/36 | |
1/3 | |
25/36 | |
11/36 |
1 - (5/6 × 5/6) = 1 - (25/36) = 11/36
Question 5 |
The probability that top and bottom cards of a randomly shuffled deck are both aces in
4/52×4/52 | |
4/52×3/52 | |
4/52×3/51 | |
4/52×4/51 |
E2 : Last card being ace
Note that E1 and E2 are dependent events, i.e., probability of last card being ace if first is ace will be lesser than the probability of last card being ace if first card is not ace.
So, probability of first card being ace = 4/52
Probability of last card being ace given that first card is ace is,
P(E2 / E1) = 3/51
∴ P(E1 and E2) = P(E1) ⋅ P(E2 / E1) = 4/52 × 3/51
Question 6 |
The probability that it will rain today is 0.5. The probability that it will rain tomorrow is 0.6. The probability that it will rain either today or tomorrow is 0.7. What is the probability that it will rain today and tomorrow?
0.3 | |
0.25 | |
0.35 | |
0.4 |
P(Tomorrow) = 0.6
P(T∪To) = 0.7
P(T∩To) = P(T) + P(To) - P(T∪To)
= 0.5 + 0.6 - 0.07
= 1.1 - 0.7
= 0.4
Question 7 |
Two people, P and Q, decide to independently roll two identical dice, each with 6 faces, numbered 1 to 6. The person with the lower number wins. In case of a tie, they roll the dice repeatedly until there is no tie. Define a trial as a throw of the dice by P and Q. Assume that all 6 numbers on each dice are equi-probable and that all trials are independent. The probability (rounded to 3 decimal places) that one of them wins on the third trial is __________.
0.021 | |
0.022 | |
0.023 | |
0.024 |
⇾ A person wins who gets lower number compared to other person.
⇾ There could be “tie”, if they get same number.
Favorable cases = {(1, 1), (2, 2), (3, 3), (4, 4), (5, 5), (6, 6)}
Probability (tie) = 6/36 (when two dice are thrown, sample space = 6 × 6 = 36)
= 1/6
“Find the probability that one of them wins in the third attempt"
⇾ Which means, first & second time it should be tie and third time it should not be tie
⇾ P (tie) * P (tie) * P (not tie)
⇒ 1/6* 1/6 * (1 - 1/6)
⇒ (5/36×6)
= 0.138/6
= 0.023
Question 8 |
A die is rolled three times. The probability that exactly one odd number turns up among the three outcomes is
1/6 | |
3/8 | |
1/8 | |
1/2 |
Total no. of possibilities are 8.
Probability of getting exactly one odd = 3/8
Question 9 |
There is a sample point at which X has the value 5. | |
There is a sample point at which X has value greater than 5. | |
There is a sample point at which X has a value greater than or equal to 5. | |
None of the above |
E(X) = x1P1 + x2P2 + ... + xnPn
In question, E(X) is given as 5.
E(X) = 5, 0≤Pi≤1
P1 + P2 + ... + Pn = 1 [Probability]
Therefore, E(X) = 5 is possible only if atleast one of the xi value is greater than 5.
Question 10 |
Consider two events E1 and E2 such that probability of E1, Pr[E1]=1/2, probability of E2, Pr[E2]=1/3, and probability of E1 and E2, Pr[E1 and E2]=1/5. Which of the following statement is/are True?
Pr[E1 or E2] is 2/3 | |
Events E1 and E2 are independent | |
Events E1 and E2 are not independent | |
Pr[E1/E2] = 4/5 |
then P(E1 and E2) = P(E1) × P(E2)
But in the given equation,
P(E1 and E2) = 1/5
P(E1) × P(E2) = 1/2 × 1/3 = 1/6
So, clearly Events E1 and E2 are not independent.
Question 11 |
E1 and E2 are events in a probability space satisfying the following constraints:
- • Pr(E1) = Pr(E2)
• Pr(E1 U E2) = 1
• E1 and E2 are independent
The value of Pr(E1), the probability of the event E1 is
0 | |
1/4 | |
1/2 | |
1 |
Pr(E1 ∪ E2) = 1
E1 and E2 are Independent.
P(E1 ∪ E2) = Pr(E1) + Pr(E2) - Pr(E1 ∩ E2)
1 = a + a - Pr(E1)⋅Pr(E2)
1 = a + a - a⋅a
2a - a2 = 1
a2 - 2a + 1 = 0
(a - 1)2 = 0
a = 1
Pr(E1) = 1
Answer: Option (D)
Question 12 |
Seven (distinct) car accidents occurred in a week. What is the probability that they all occurred on the same day?
1/77 | |
1/76 | |
1/27 | |
7/27 |
Such as total no. of days in a week = 7
Total probability = 7 × 1/77 = 1/76
Question 13 |
Four fair coins are tossed simultaneously. The probability that at least one head and one tail turn up is
1/16 | |
1/8 | |
7/8 | |
15/16 |
Atleast one head = 1/16
Atleast one tail = 1/16
Probability of getting one head and one tail is = 1 - 1/16 - 1/16 = 16 - 1 - 1/16 = 14/16 = 7/8
Question 14 |
Let P(E) denote the probability of the event E. Given P(A) = 1, P(B) = 1/2, the values of P(A|B) and P(B|A) respectively are
1/4, 1/2 | |
1/2, 1/4 | |
1/2, 1 | |
1, 1/2 |
P(A/B) = P(A∩B)/P(B)
= P(A)⋅P(B)/P(B) (consider P(A), P(B) are two independent events)
= 1
P(B/A) = P(B∩A)/P(A)
= P(B)⋅P(A)/P(A)
= 1/2
Question 15 |
A program consists of two modules executed sequentially. Let f1(t) and f2(t) respectively denote the probability density functions of time taken to execute the two modules. The probability density function of the overall time taken to execute the program is given by:
f1(t) + f2(t) | |
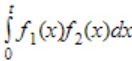 | |
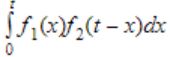 | |
max{f1(t), f2(t)} |
→ They representing the probability density functions of time taken to execute.
→ f1 can be executed in 'x' time.
f2 can be executed in 't-x' time.
→ The probability density function =
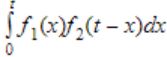
Question 16 |
If a fair coin is tossed four times. What is the probability that two heads and two tails will result?
3/8 | |
1/2 | |
5/8 | |
3/4 |
Then total number of possibilities = 24 = 16
No. of possibilities getting 2 heads and 2 tails is
HHTT, HTHT, TTHH, THTH, THHT, HTTH = 6
Probability of getting 2 heads and 2 tails is
= No. of possibilities/Total no. of possibilities = 6/16 = 3/8
Question 17 |
An examination paper has 150 multiple-choice questions of one mark each, with each question having four choices. Each incorrect answer fetches -0.25 mark. Suppose 1000 students choose all their answers randomly with uniform probability. The sum total of the expected marks obtained by all these students is:
0 | |
2550 | |
7525 | |
9375 |
Probability of selecting a wrong answer = 3/4
For correct answer +1, for wrong answer-0.25;
Expected marks for each question = (1/4) × 1 + (3/4) -(0.25)
= 1/4 + (-3/16)
= 4-3/16
= 1/16
= 0.0625
Expected marks for 150 questions = 150 × 0.625 = 9.375
The sum total of expected marks obtained by 1000 students is = 1000×9.375 = 9375
Question 18 |
Two n bit binary strings, S1 and S2, are chosen randomly with uniform probability. The probability that the Hamming distance between these strings (the number of bit positions where the two strings differ) is equal to d is
nCd /2n
| |
nCd / 2d | |
d/2n | |
1/2d |
Total no. of cases where n positions have any binary bit = 2n
The probability of 'd' bits differ = nCd / 2n
Question 19 |
A point is randomly selected with uniform probability in the X-Y plane within the rectangle with corners at (0,0), (1,0), (1,2) and (0,2). If p is the length of the position vector of the point, the expected value of p2 is
2/3 | |
1 | |
4/3 | |
5/3 |
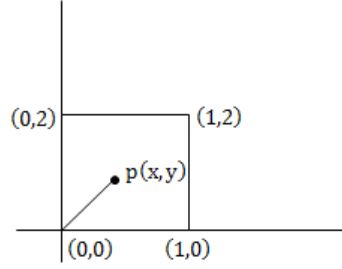
Above diagram shows the scenario of our question.
The length p of our position vector (x,y) is
p = √x2 + y2
p2 = x2 + y2
E(p2) = E(x2 + y2) = E(x2) + E(y2)
Now we need to calculate the probability density function of X and Y.
Since distribution is uniform,
X goes from 0 to 1, so PDF(x) = 1/1-0 = 1
Y goes from 0 to 2, so PDF(y) = 1/2-0 = 1/2
Now we evaluate,
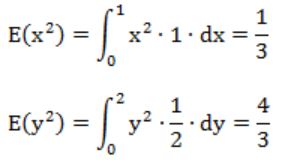
E(p2) = E(x2) + E(y2) = 5/3
Question 20 |
Let A and B be any two arbitrary events, then, which one of the following is true?
P(A∩B) = P(A)P(B) | |
P(A∪B) = P(A) + P(B) | |
P(A|B) = P(A∩B)P(B) | |
P(A∪B) ≤ P(A) + P(B) |
(B) Happens when A and B are mutually exclusive.
(C) Not happens.
(D) P(A∪B) ≤ P(A) + P(B) is true because P(A∪B) = P(A) + P(B) - P(A∩B).
Question 21 |
The probability of an event B is P1. The probability that events A and B occur together is P2 while the probability that A and ![]() occur together is P3. The probability of the event A in terms of P1, P2 and P3 is __________.
occur together is P3. The probability of the event A in terms of P1, P2 and P3 is __________.
P2 + P3 |
P3 = P(A) - P2
P(A) = P2 + P3
Question 22 |
Let A, B and C be independent events which occur with probabilities 0.8, 0.5 and 0.3 respectively. The probability of occurrence of at least one of the event is __________
0.93 |
Since all the events are independent, so we can write
P(A∪B∪C) = P(A) + P(B) + P(C) - P(A)P(B) - P(B)P(C) - P(A)P(C) + P(A)P(B) P(C)
= 0.8 + 0.5 + 0.3 - 0.4 - 0.5 - 0.24 + 0.12
= 0.93
Question 23 |
Let X and Y be two exponentially distributed and independent random variables with mean α and β, respectively. If Z = min(X,Y), then the mean of Z is given by
1/α+β | |
min(α, β) | |
αβ/α + β | |
α + β |
Question 24 |
In how many ways can we distribute 5 distinct balls, B1, B2, …, B5 in 5 distinct cells, C1, C2, …, C5 such that Ball B, is not in cell Ci, ∀i = 1, 2, …, 5 and each cell contains exactly one ball?
44 | |
96 | |
120 | |
3125 |
∠5(1 - 1/∠1 + 1/∠2 - 1/∠3 + 1/∠4 - 1/∠5)
= 44
Question 25 |
A bag contains 10 blue marbles, 20 green marbles and 30 red marbles. A marble is drawn from the bag, its colour recorded and it is put back in the bag. This process is repeated 3 times. The probability that no two of the marbles drawn have the same colour is
1/36 | |
1/6 | |
1/4 | |
1/3 |
Total possible combinations = 3! = 6
Probability of blue marble = 10/60[10 + 20 + 30 = 60]
Probability of green marble = 20/60
Probability of red marble = 30/60
The probability that no two of the marbles has same colour = [10/60 * 20/60 * 30/60] = 1/6
Question 26 |
An unbiased coin is tossed repeatedly until the outcome of two successive tosses is the same. Assuming that the trials are independent, the expected number of tosses is
3 | |
4 | |
5 | |
6 |
The expected number of coin flips for getting n consecutive heads is(2^(n+1) -2)
The expected number of coin flips for getting n consecutive heads is(2^(n+1) -2)
The expected number of coin flips for getting n consecutive same tosses is (2^(n+1) -2) / 2.
where n = 2,
which is (2^(3+1) - 2) / 2 = 3
Question 27 |
In a certain town, the probability that it will rain in the afternoon is known to be 0.6. Moreover, meteorological data indicates that if the temperature at noon is less than or equal to 25°C, the probability that it will rain in the afternoon is 0.4. The temperature at noon is equally likely to be above 25°C, or at/below 25°C. What is the probability that it will rain in the afternoon on a day when the temperature at noon is above 25°C?
0.4 | |
0.6 | |
0.8 | |
0.9 |
0.6 = (0.5×0.4) + (0.5×P(rain at temp>25)
0.6 = (2) + (0.5×P(rain at temp>25)
P(rain at temp>25) = 0.8
Question 28 |
When a coin is tossed, the probability of getting a Head is p, 0 < p < 1. Let N be the random variable denoting the number of tosses till the first Head appears, including the toss where the Head appears. Assuming that successive tosses are independent, the expected value of N is
1/p | |
1/(1-p) | |
1/p2 | |
1/(1-p2) |
Multiply both sides with (1 - p) and subtract,
E - (1 - p) E = 1 × p + (1 - p) p + (1 - p) (1 - p) p + ......
E - (1 - p) E = p/(1 - (1 - p))
(1 - 1 + p) E = 1
pE = 1
E = 1/p
Question 29 |
Suppose there are two coins. The first coin gives heads with probability 5/8 when tossed, while the second coin gives heads with probability 1/4. One of the two coins is picked up at random with equal probability and tossed. What is the probability of obtaining heads ?
7/8 | |
1/2 | |
7/16 | |
5/32 |
The probability of obtaining heads
= (1/2)(5/8) + (1/2)(1/4)
= (5/16) + (1/8)
= 7/16
Question 30 |
Consider a hash function that distributes keys uniformly. The hash table size is 20. After hashing of how many keys will the probability that any new key hashed collides with an existing one exceed 0.5.
5 | |
6 | |
7 | |
10 |
Probability of collision for each entry = 1/20
After inserting X values then probability becomes 1/2
i.e., (1/20)X = 1/2
X = b
Question 31 |
In a multi-user operating system on an average, 20 requests are made to use a particular resource per hour. The arrival of requests follows a Poisson distribution. The probability that either one, three or five requests are made in 45 minutes is given by :
6.9 × 106 × e-20 | |
1.02 × 106 × e-20 | |
6.9 × 103 × e-20 | |
1.02 × 103 × e-20 |
So, λ=15
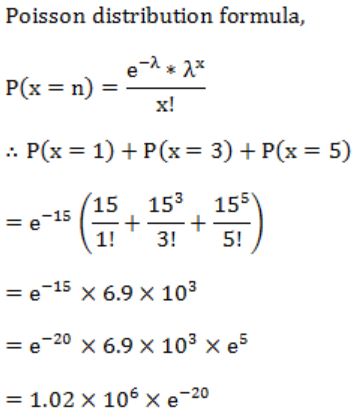
Question 32 |
A sample space has two events A and B such that probabilities P(A ∩ B) = 1/2, P(A') = 1/3, P(B') = 1/3. What is P(A ∪ B)?
11/12 | |
10/12 | |
9/12 | |
8/12 |
P(A') = 1/3; P(A) = 2/3
P(B') = 1/3; P(B) = 2/3
P(A ∪ B) = P(A) +P(B) - P(A ∩ B)
= 2/3 + 2/3 - 1/2
= 4+4-3/ 6
= 5/6
= 10/12
Question 33 |
What is the probability that in a randomly chosen group of r people at least three people have the same birthday?
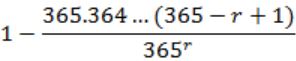 | |
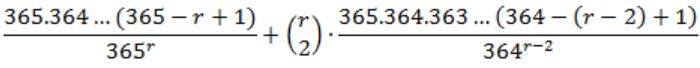 | |
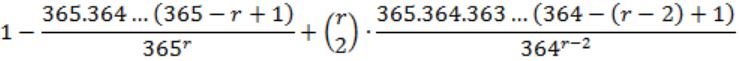 | |
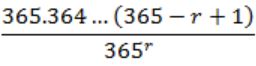 |
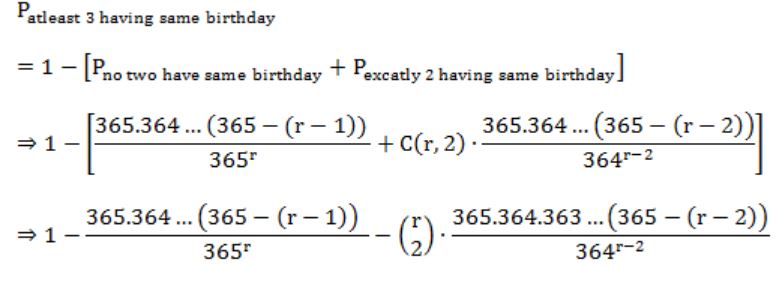
Question 34 |
Which of the following statements are FALSE?
For poisson distribution, the mean is twice the variance. | |
In queuing theory, if arrivals occur according to poisson distribution, then the inter-arrival time is exponentially distributed. | |
The distribution of waiting time is independent of the service discipline used in selecting the waiting customers for service. | |
If the time between successive arrivals is exponential, then the time between the occurrences of every third arrival is also exponential. | |
Both (A) and (C). |
Option C is also False, because waiting time is dependent on the service discipline.
Question 35 |
Let f(x) be the continuous probability density function of a random variable X. The probability that a < X ≤ b, is:
f(b - a)
| |
f(b) - f(a) | |
 | |
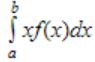 |
Then the probablity be area of the corresponding curve i.e.,

Question 36 |
Box P has 2 red balls and 3 blue balls and box Q has 3 red balls and 1 blue ball. A ball is selected as follows:
(i) Select a box
(ii) Choose a ball from the selected box such that each ball in
the box is equally likely to be chosen. The probabilities of
selecting boxes P and Q are (1/3) and (2/3), respectively.
Given that a ball selected in the above process is a red ball, the probability that it came from the box P is
4/19 | |
5/19 | |
2/9 | |
19/30 |
Q → 3 red, 1 blue
The probability of selecting a red ball is
(1/3)(2/5) + (2/3)(3/4)
2/15 + 1/2 = 19/30
The probability of selecting a red ball from P
(1/3) * (2/5) = 2/15
→ The colour of ball is selected is to be red and that is taken from the box P.
⇒ Probability of selecting a red ball from P/Probability of selecting a red ball
⇒ (2/15)/(19/30)
⇒ 4/19
Question 37 |
A random bit string of length n is constructed by tossing a fair coin n times and setting a bit to 0 or 1 depending on outcomes head and tail, respectively. The probability that two such randomly generated strings are not identical is:
1/2n | |
1 - 1/n | |
1/n! | |
1-(1/2n) |
Hence Probability = (2n - 1) /2n = 1 - 1/2n
Question 38 |
P and Q are considering to apply for job. The probability that p applies for job is 1/4. The probability that P applies for job given that Q applies for the job 1/2 and The probability that Q applies for job given that P applies for the job 1/3.The probability that P does not apply for job given that Q does not apply for the job
 | |
 | |
 | |
 |
Probability that ‘P’ applies for the job given that Q applies for the job = P(p/q) = 1/2 ⇾ (2)
Probability that ‘Q’ applies for the job, given that ‘P’ applies for the job = P(p/q) = 1/3 ⇾ (3)
Bayes Theorem:
(P(A/B) = (P(B/A)∙P(A))/P(B) ; P(A/B) = P(A∩B)/P(B))
⇒ P(p/q) = (P(q/p)∙P(p))/p(q)
⇒ 1/2 = (1/3×1/4)/p(q)
p(q) = 1/12×2 = 1/(6) (P(q) = 1/6) ⇾ (4)
From Bayes,
P(p/q) = (P(p∩q))/(P(q))
1/2 = P(p∩q)/(1⁄6)
(p(p∩q) = 1/12)
We need to find out the “probability that ‘P’ does not apply for the job given that q does not apply for the job = P(p'/q')
From Bayes theorem,
P(p'/q') = (P(p'∩q'))/P(q') ⇾ (5)
We know,
p(A∩B) = P(A) + P(B) - P(A∪B)
also (P(A'∩B') = 1 - P(A∪B))
P(p'∩q') = 1 - P(p∪q)
= 1 - (P(p) + P(q) - P(p∩q))
= 1 - (P(p) + P(q) - P(p) ∙ P(q))
= 1 - (1/4 + 1/6 - 1/12)
= 1 - (10/24 - 2/24)
= 1 - (8/24)
= 2/3
(P(p'∩q') = 2/3) ⇾ (6)
Substitute in (5),
P(p'⁄q') = (2⁄3)/(1-P(q)) = (2⁄3)/(1-1/6) = (2⁄3)/(5⁄6) = 4/5
(P(p'/q') = 4/5)
