HCU PHD CS 2018 December
Question 1 |
A pilgrim covers half of his journey by bus at 60 km/h, two thirds of the remainder by auto at 20 km/h and the rest by walk at 4 km/h. The average speed of the tourist in km/h during his entire journey is
12 | |
15 | |
20 | |
25 | |
24 |
Question 1 Explanation:
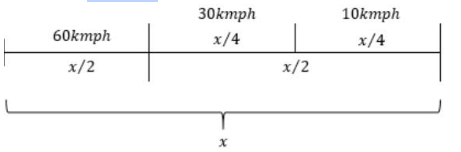
Let ‘x’ be the total distance,
Speed = distance/ time
Total speed = (total distance)/(total time); Time =distance/speed
Time taken for train journey = (x⁄2)/60kmph=x/120
Time taken for bus journey = (x⁄4)/30kmph=x/120
Time taken for cycle journey = (x⁄4)/10kmph=x/40
Total time = x/120+x/120+x/40=5x/120
Total speed = (total distance)/(total time)=x/(5x⁄120)=(120×x)/5x=24kmph
Question 2 |
The number of divisors of 2022 is
6 | |
7 | |
8 | |
3 |
Question 2 Explanation:
The number of divisors are 8.
1, 2, 3, 6, 337, 674, 1011 and 2022
1, 2, 3, 6, 337, 674, 1011 and 2022
Question 3 |
The product of the ages of ravi and ramu is 260. If twice the age Ravi is more than ram's age by 6 years, what is Ravi's age?
16 | |
14 | |
12 | |
13 |
Question 3 Explanation:
B ⟶ A
A ⟶ C
BC ⟶ D
AC ⟶ BE
B+ = BACDE
A+ = ACBED
So A & B are candidate keys.
There is no partial dependency so in 2NF.
But in the BC⟶D, neither BC is key nor D is prime attribute hence not in 3NF.
A ⟶ C
BC ⟶ D
AC ⟶ BE
B+ = BACDE
A+ = ACBED
So A & B are candidate keys.
There is no partial dependency so in 2NF.
But in the BC⟶D, neither BC is key nor D is prime attribute hence not in 3NF.
Question 4 |
The value of the expression 12112(mod 17)
1 | |
4 | |
13 | |
16 |
Question 4 Explanation:
12112(mod 17)=1.
Question 5 |
How many positive integers less than 1000 are co-prime with 14?
571 | |
142 | |
429 | |
None of the these |
Question 5 Explanation:
14 can be written as 7×2. So any no. which is co-prime to 14 should not be divisible by 7 nor divisible by 2.
Let’s first find no. of numbers divisible by 7 or 2.
Let the no. of numbers divisible by 7 is A, and no. of numbers divisible by 2 is B.
Now no. numbers divisible by 7,
A = 999/7 = 142
No. of numbers divisible by 2 is,
B = 999/2 = 499
No. of numbers divisible by both 7 and 2, i.e., 14
A∩B = 999/14 = 71
∴ No. of numbers divisible by 7 or 2 is
A∪B = A + B - A∩B = 142 + 499 - 71 = 570
∴ No. of numbers that are coprime to 14 are,
999 - 570 = 429
Let’s first find no. of numbers divisible by 7 or 2.
Let the no. of numbers divisible by 7 is A, and no. of numbers divisible by 2 is B.
Now no. numbers divisible by 7,
A = 999/7 = 142
No. of numbers divisible by 2 is,
B = 999/2 = 499
No. of numbers divisible by both 7 and 2, i.e., 14
A∩B = 999/14 = 71
∴ No. of numbers divisible by 7 or 2 is
A∪B = A + B - A∩B = 142 + 499 - 71 = 570
∴ No. of numbers that are coprime to 14 are,
999 - 570 = 429
Question 6 |
There are 25 horses which you need to find out the fastest 3 horses. You can conduct race among at most 5 to find out their relative speed. At no point you can find out the actual speed of the horse in a race. find out how many races are required to get the top 3 horses.
5 | |
6 | |
7 | |
8 |
Question 6 Explanation:
Divide all the 25 horses into 5 groups of five each .Then conduct races between the horses of each group and choose the fastest horse of each group.Till now 5 races are conducted. NOw we left with a total of 5 fastest horses and then at last conducted one more race between the remaining horses and chose the three fastest. So this is how three fastest horses are selected with a total 5 races.
Question 7 |
A cube of side 1 unit is placed in such a way that the origin coincides with one of its vertices and the three(positive) axes along three of its edges. What are the coordinates of the vertex which is diagonally opposite to the vertex whose coordinates are (1,0,1)?
(0,0,0) | |
(1,1,0) | |
(0,1,0)
| |
(1,1,1) |
Question 7 Explanation:

∴ The coordinates of the vertex which is diagonally opposite to the vertex whose coordinates are (1,0,1) is (0,1,0).
Question 8 |
If pqr ≠ 0 and p-x =1/q, q-y =1/r, r-z =1/p, what is the value of the product xyz?
-1 | |
1/pqr | |
1 | |
pqr |
Question 8 Explanation:
pqr≠0
→ p-x = 1/q ⟹ 1/px = 1/q
⟹ q = px
⟹ log q = log px
⟹ x log p = log q
⟹ x = log q/ log p
→ q-y = 1/r ⟹ 1/qy = 1/r
⟹ qy = r
⟹ y log q = log r
⟹ y = log r/ log q
→ r-z = 1/p ⟹ 1/rz = 1/p
⟹ p = rz
⟹ log rz = log p
⟹ z log r = log p
⟹ z = log p/ log r
XYZ = log q/ log p * log r/ log q * log p/ log r =1
→ p-x = 1/q ⟹ 1/px = 1/q
⟹ q = px
⟹ log q = log px
⟹ x log p = log q
⟹ x = log q/ log p
→ q-y = 1/r ⟹ 1/qy = 1/r
⟹ qy = r
⟹ y log q = log r
⟹ y = log r/ log q
→ r-z = 1/p ⟹ 1/rz = 1/p
⟹ p = rz
⟹ log rz = log p
⟹ z log r = log p
⟹ z = log p/ log r
XYZ = log q/ log p * log r/ log q * log p/ log r =1
Question 9 |
The minimum number of cards to e dealt from an arbitrarily shuffled deck of 52 cards to guarantee that three cards are with same number is
14 | |
27 | |
30 | |
39 | |
None of the above |
Question 9 Explanation:
We know that in a deck of 52 cards there are 4 suits.
Now to guarantee that three cards are from same suit,
⇒ Let's first draw 4 cards of different sizes.
⇒ Now again draw 4 cards of different suits. Now we have 8 cards of 2 cards from each suit.
⇒ Now take 1 card from any suit, which will guarantee that 3 cards are from the same suit.
So, in total 9 cards are required.
Now to guarantee that three cards are from same suit,
⇒ Let's first draw 4 cards of different sizes.
⇒ Now again draw 4 cards of different suits. Now we have 8 cards of 2 cards from each suit.
⇒ Now take 1 card from any suit, which will guarantee that 3 cards are from the same suit.
So, in total 9 cards are required.
Question 10 |
A container originally contains 10 litres of pure spirit. From this container 1 litre of spirit is replaced with 1 litre of water. Subsequently, 1 litre of the mixture is again replaced with 1 litre of water and this process is replaced is repeated one more time. how much spirit is now left in the container?
7 litre | |
7.21 litres | |
7.29 litres | |
7.31 litres
|
Question 10 Explanation:
10(729/1000×1=7.29 litres)
Question 11 |
Please answer the following questions Q11-13 based on the flowchart given below:
Note: Here T0 represents the least significant bit; C,S,T are stored in consecutive 9 bits where each variable can be accessed independently and shift operation is performed on the 9 bits representing C,S,T.

If the values of P and T are 1011 and 1101, respectively, then the contents of S and T at the end of execution are
S=101, T=1111 | |
S=1000, T=1111 | |
S=1010, T=1110 | |
S=1010, T=1100
|
Question 12 |
Please answer the following questions Q11-13 based on the flowchart given below:
Note: Here T0 represents the least significant bit; C,S,T are stored in consecutive 9 bits where each variable can be accessed independently and shift operation is performed on the 9 bits representing C,S,T.

What kind of operation the flowchart performs?
unsigned binary Division | |
Signed binary Division | |
Unsigned binary multiplication | |
Signed binary Multiplication |
Question 13 |
Please answer the following questions Q11-13 based on the flowchart given below:
Note: Here T0 represents the least significant bit; C,S,T are stored in consecutive 9 bits where each variable can be accessed independently and shift operation is performed on the 9 bits representing C,S,T.

Given that T=1010, the number of shift right operations performed is?
1 | |
2 | |
3 | |
4 |
Question 14 |
What would be the smallest natural number which when divided by any of the numbers 20,44 and 76 leaves a remainder 7 in each case is,
4187 | |
6047 | |
7987 | |
63847 |
Question 14 Explanation:
Find the LCM of 20, 42 and 76.
20 = 2x2x5
42 = 2x3x7
76 = 2x2x19
The LCM is 2x2x3x5x7x19 = 7980.
Next add 7 to 7980 to get 7987 as the answer.
20 = 2x2x5
42 = 2x3x7
76 = 2x2x19
The LCM is 2x2x3x5x7x19 = 7980.
Next add 7 to 7980 to get 7987 as the answer.
Question 15 |
25 people are in a room. 15 of them play hockey, 17 of them play football, 5 of them play chess, 13 of them play both hockey and football, 2 of them play both chess hockey, 2 of them play both football and chess and none play all three games. then the number of persons who play neither hockey nor football nor chess is:
4 | |
5 | |
7 | |
8 |
Question 15 Explanation:
Let A be the people who play hockey.
Let B be the people who play football.
Let C be the people who play chess.
Now, according to question
A = 15
B = 17
C = 5
A ∩ B = 13
A ∩ C = 2
B ∩ C = 2
A ∩ B ∩ C =0
And we have to find,
A’ ∩ B’ ∩ C’ = (A∪B∪C)’ = 25 - (A∪B∪C)
Now let’s first find A∪B∪C,
A∪B∪C = A + B + C - (A∩B) - (B∩C) - (C∩A) + (A∩B∩C)
= 15 + 17 + 5 - 13 - 2 - 2 + 0
= 37 - 17
= 20
∴ The answer will be,
25 - 20 = 5
Let B be the people who play football.
Let C be the people who play chess.
Now, according to question
A = 15
B = 17
C = 5
A ∩ B = 13
A ∩ C = 2
B ∩ C = 2
A ∩ B ∩ C =0
And we have to find,
A’ ∩ B’ ∩ C’ = (A∪B∪C)’ = 25 - (A∪B∪C)
Now let’s first find A∪B∪C,
A∪B∪C = A + B + C - (A∩B) - (B∩C) - (C∩A) + (A∩B∩C)
= 15 + 17 + 5 - 13 - 2 - 2 + 0
= 37 - 17
= 20
∴ The answer will be,
25 - 20 = 5
Question 16 |
There are 5 bags labeled 1 to 5. All the coins in a given bag have the same weight. Some bags have coins of weight 10 gm, others have coins of weight 11 gm. 1 pick 1,2,4,8,16 coins respectively from bags 1 to 5. Their total weight comes out to 323 gm. Then the labels of the bags having 11 gm coins is
1,2,5 | |
2,3,4 | |
1,3,4 | |
2,3,5 |
Question 16 Explanation:
Bags: 1 2 3 4 5
No. of coins picked: 1 2 4 8 16
There are two types of weights of coin, i.e., 10gm and 11gm. And the total weight of picked coins is 323gm.
Let there be x number of 10gm coins and y number of 11gm coins.
So, 10x + 11y = 323 ------ (1)
And we also know that total number of coins picked is
1 + 2 + 4 + 8 + 16 = 31 which is equal to x + y, so,
= 31 ------ (2)
Solving equation (1) and (2), we get
y = 13
Means total there are 13 coins of 11gm.
Now we can choose bag number 1, 3 and 4, we will get a total sum of 13 coins picked from them.
So product of labelled bag number = 1×3×4 = 12
No. of coins picked: 1 2 4 8 16
There are two types of weights of coin, i.e., 10gm and 11gm. And the total weight of picked coins is 323gm.
Let there be x number of 10gm coins and y number of 11gm coins.
So, 10x + 11y = 323 ------ (1)
And we also know that total number of coins picked is
1 + 2 + 4 + 8 + 16 = 31 which is equal to x + y, so,
= 31 ------ (2)
Solving equation (1) and (2), we get
y = 13
Means total there are 13 coins of 11gm.
Now we can choose bag number 1, 3 and 4, we will get a total sum of 13 coins picked from them.
So product of labelled bag number = 1×3×4 = 12
Question 17 |
Two parallel chords of length 30cm and 16cm are drawn on the opposite sides of the center of a circle with radius 17cm. The distance between the chords is
23cm | |
21cm | |
19cm | |
none of the above |
Question 17 Explanation:

A = distance of chord of length 30cm from the centre
B = distance of chord of length 16cm from the centre
Now,
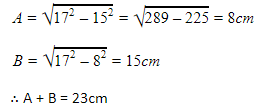
Question 18 |
In the year 1980, the age (in years) of a person was 1/89th of his year of birth. What is the age (in years) of this person in 2018?
54 | |
64 | |
80 | |
60 |
Question 18 Explanation:
Let the year of birth of a person be x, then according to the question,


Question 19 |
Read the passage carefully and answer Questions Q19-22.
The problem of heuristic programming-of making computers solve really difficult problems- are divided into five main areas. Search, pattern recognition, Learning, Planning, and Induction. Whenever appropriate, the discussion is supported by extensive citation of the literature and by descriptions of a few of the most successful heuristic (Problem-solving) programs constructed to date.
The adjective "heuristic," as used here and widely in the literature, means related to improving problem-solving performance; as a noun it is also used in regard to any method or trick used to improve the efficiency of a problem-solving system. A "heuristic program," to be considered successful, must work well on a variety of problems, and may often be executed if it fails on some. We often find it worthwhile to introduce a heuristic method, which happens to cause occasional failures, if there is an overall improvement in performance. But imperfect methods are not necessarily heuristic, nor vice versa. Hence “heuristic” should not be regarded as opposite to “foolproof”; this has caused some confusion in the literature.
What is heuristic programming?
Making computers solve hard problems | |
Making computers do patterns recognition | |
Making computers solve problems by searching for a solution | |
Programming a unique solution to a hard problems |
There are 19 questions to complete.
