Contest-Free-Grammar
Question 1 |
Let G = ({S},{a,b},R,S) be a context free grammar where the rule set R is S → aSb | SS | ε Which of the following statements is true?
G is not ambiguous | |
There exist x, y ∈ L(G) such that xy ∉ L(G)
| |
There is a deterministic pushdown automaton that accepts L(G) | |
We can find a deterministic finite state automaton that accepts L(G) |
Question 1 Explanation:
a) False
We can derive ϵ with more than one parse tree,
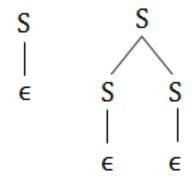
So ambiguous.
b) False
Let take x=aabb and y=ab then xy=aabbab we can produce it,

c) True
Because the language generated is no. of a's = no' of b's. So DPDA exist for this language.
d) Not possible.
Infinite memory needed to count 'a' for no. of 'b'.
We can derive ϵ with more than one parse tree,

So ambiguous.
b) False
Let take x=aabb and y=ab then xy=aabbab we can produce it,

c) True
Because the language generated is no. of a's = no' of b's. So DPDA exist for this language.
d) Not possible.
Infinite memory needed to count 'a' for no. of 'b'.
Question 2 |
For a context-free grammar, FOLLOW(A) is the set of terminals that can appear immediately to the right of non-terminal A in some "sentential" form. We define two sets LFOLLOW(A) and RFOLLOW(A) by replacing the word "sentential" by "left sentential" and "right most sentential" respectively in the definition of FOLLOW(A).
Which of the following statements is/are true?
Which of the following statements is/are true?
FOLLOW(A) and FOLLOW(A) may be different | |
FOLLOW(A) and FOLLOW(A) are always the same | |
All the three sets are identical | |
All the three sets are different |
Question 2 Explanation:
LFOLLOW may be different but RFOLLOW and FOLLOW will be same.
There are 2 questions to complete.
