Grammar
Question 1 |
In the following grammar
X ::= X ⊕ Y/Y
Y ::= Z * Y/Z
Z ::= id
Which of the following is true?
‘⊕’ is left associative while ‘*’ is right associative | |
Both ‘⊕’ and ‘*’ is left associative | |
‘⊕’ is right associative while ‘*’ is left associative | |
None of the above |
Question 1 Explanation:
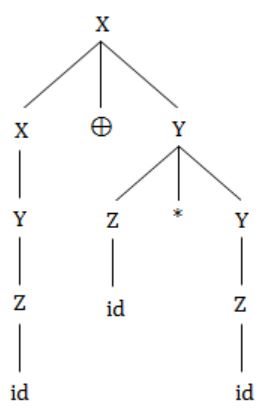
⊕ is left associative.
* is right associative.
Question 2 |
A grammar that is both left and right recursive for a non-terminal, is
Ambiguous | |
Unambiguous | |
Information is not sufficient to decide whether it is ambiguous or unambiguous | |
None of the above |
Question 2 Explanation:
If a grammar is both left and right recursion, then grammar may or may not be ambiguous.
Question 3 |
Given the following expression grammar:
E → E * F | F + E | F
F → F - F | id
which of the following is true?
* has higher precedence than + | |
- has higher precedence than * | |
+ and – have same precedence | |
+ has higher precedence than * |
Question 3 Explanation:
The operator which is in low level that can have high preference.
Order of precedence is *, +, -.
Here * and + have equal preference, '-' can have higher precedence than + and *.
Order of precedence is *, +, -.
Here * and + have equal preference, '-' can have higher precedence than + and *.
There are 3 questions to complete.
