Graphs
Question 1 |
Consider a simple connected graph G with n vertices and n-edges (n>2). Then, which of the following statements are true?
G has no cycles. | |
The graph obtained by removing any edge from G is not connected. | |
G has at least one cycle. | |
The graph obtained by removing any two edges from G is not connected. | |
Both C and D. |
For example let us consider, n=3.
Question 2 |
The number of articulation points of the following graph is

0 | |
1 | |
2 | |
3 |
Total no. of articulation points = 3
Question 3 |
Let G be an undirected graph. Consider a depth-first traversal of G, and let T be the resulting depth-first search tree. Let u be a vertex in G and let ν be the first new (unvisited) vertex visited after visiting u in the traversal. Which of the following statements is always true?
{u, v} must be an edge in G, and u is a descendant of v in T | |
{u, v} must be an edge in G, and v is a descendant of u in T | |
If {u, v} is not an edge in G then u is a leaf in T | |
If {u, v} is not an edge in G then u and v must have the same parent in T |
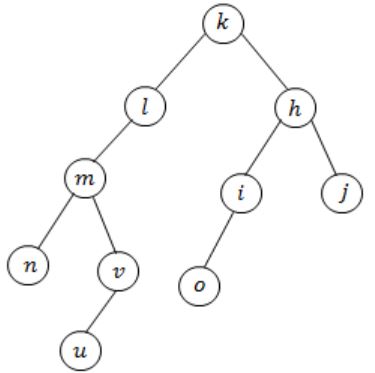
In DFS after visiting u, there is no child node then back tracking is happen and then visit the node v. There is no need of (u,v) be an edge.
Question 4 |
Consider an undirected unweighted graph G. Let a breadth-first traversal of G be done starting from a node r. Let d(r,u) and d(r,v) be the lengths of the shortest paths from r to u and v respectively in G. If u is visited before v during the breadth-first traversal, which of the following statements is correct?
d(r,u) | |
d(r,u)>d(r,v) | |
d(r,u)≤d(r,v) | |
None of the above |
Question 5 |
(I) No edge of G is a cross edge with respect to TD.(A cross edge in G is between two nodes neither of which is an ancestor of the other in TD.)
(II) For every edge (u,v) of G, if u is at depth i and v is at depth j in TB, then ∣i−j∣ = 1.
Which of the statements above must necessarily be true?
I only | |
II only | |
Both I and II | |
Neither I nor II |
II. Just draw a triangle ABC. Source is A. Vertex B and C are at same level at distance 1.
There is an edge between B and C too. So here |i - j| = |1 - 1| = 0. Hence, False.
Question 6 |
How many edges are there in a forest with p components having n vertices in all?
n-p |
Now, '0' edges for p-1 vertices (p-1 components) and n-p edges for n-p+1 vertices (1 component).
So, total of n-p edges for p components.
Question 7 |
A sink in a directed graph is a vertex i such that there is an edge from every vertex j ≠ i to i and there is no edge from i to any other vertex. A directed graph G with n vertices is represented by its adjacency matrix A, where A[i] [j] = 1 if there is an edge directed from vertex i to j and 0 otherwise. The following algorithm determines whether there is a sink in the graph G.
i = 0
do {
j = i + 1;
while ((j < n) && E1)
j++;
if (j < n) E2;
} while (j < n);
flag = 1;
for (j = 0; j < n; j++)
if ((j! = i) && E3)
flag = 0;
if (flag)
printf("Sink exists");
else
printf ("Sink does not exist");
Choose the correct expressions for E1 and E2
E1 : A[i][j] and E2 : i = j; | |
E1 : !A[i][j] and E2 : i = j + 1; | |
E1: !A[i][j] and E2 : i = j; | |
E1 : A[i][j] and E2 : i = j + 1; |
The first part of the code, is finding if there is any vertex which doesn't have any outgoing edge to any vertex coming after it in adjacency matrix. The smart part of the code is E2, which makes rows slip when there is no edge from i to it, making it impossible for them to form a sink. This is done through
E1: A[i][j]
and
E2: i = j
E1 makes sure that there is no edge from i to j and i is a potential sink till A[i][j] becomes 1. If A[i][j] becomes 1, i can no longer be a sink. Similarly, all previous j can also not be a sink. Now, the next potential candidate for sink is j. So, in E2, we must make i = j.
So, answer is (C).
Question 8 |
A sink in a directed graph is a vertex i such that there is an edge from every vertex j ≠ i to i and there is no edge from i to any other vertex. A directed graph G with n vertices is represented by its adjacency matrix A, where A[i] [j] = 1 if there is an edge directed from vertex i to j and 0 otherwise. The following algorithm determines whether there is a sink in the graph G.
i = 0
do {
j = i + 1;
while ((j < n) && E1) j++;
if (j < n) E2;
} while (j < n);
flag = 1;
for (j = 0; j < n; j++)
if ((j! = i) && E3)
flag = 0;
if (flag)
printf("Sink exists");
else
printf("Sink does not exist");
Choose the correct expressions for E3
(A[i][j] && !A[j][i]) | |
(!A[i][j] && A[j][i]) | |
(!A[i][j] | | A[j][i]) | |
(A[i][j] | | !A[j][i]) |
Now, the loop breaks when we found a potential sink-that is a vertex which does not have any outgoing edge to any coming after it in adjacency matrix.
So, if the column in which this vertex comes is all 1's and the row is all 0's (except diagonal), this is the sink. Otherwise there is no sink in the graph. So, E3 is checking this condition. But in the code flag is used for storing the state that sink is present or not. And as per the usage of flag in code, by default sink is considered present.
So, the condition is E3 must make flag = 0, if the found i is not a sink. So, the condition should be
A[i][j] | | !A[j][i]
So, option (D) is the answer.
Question 9 |
Consider a simple graph with unit edge costs. Each node in the graph represents a router. Each node maintains a routing table indicating the next hop router to be used to relay a packet to its destination and the cost of the path to the destination through that router. Initially, the routing table is empty. The routing table is synchronously updated as follows. In each updation interval, three tasks are performed.
1. A node determines whether its neighbours in the graph are accessible. If so, it sets the tentative cost to each accessible neighbour as 1. Otherwise, the cost is set to ∞.
2. From each accessible neighbour, it gets the costs to relay to other nodes via that neighbour (as the next hop).
3. Each node updates its routing table based on the information received in the previous two steps by choosing the minimum cost.
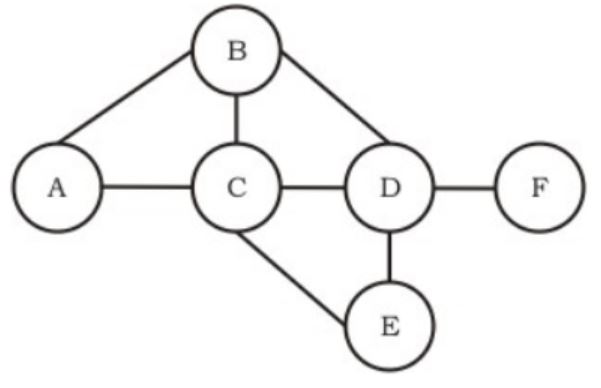
For the graph given above, possible routing tables for various nodes after they have stabilized, are shown in the following options. Identify the correct table.
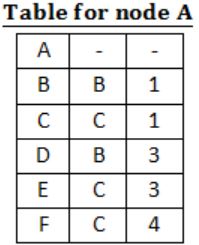 | |
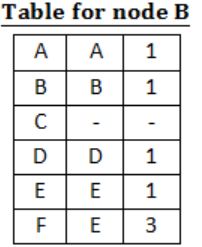 | |
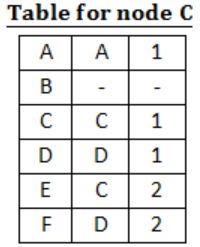 | |
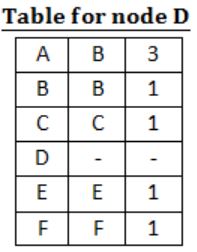 |
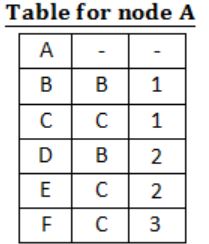
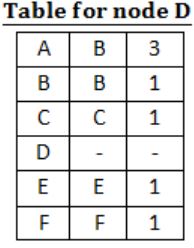
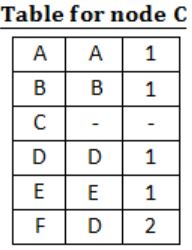
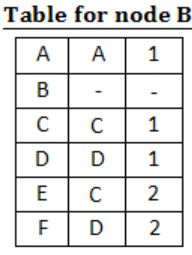
Question 10 |
Consider a simple graph with unit edge costs. Each node in the graph represents a router. Each node maintains a routing table indicating the next hop router to be used to relay a packet to its destination and the cost of the path to the destination through that router. Initially, the routing table is empty. The routing table is synchronously updated as follows. In each updation interval, three tasks are performed.
1. A node determines whether its neighbours in the graph are accessible. If so, it sets the tentative cost to each accessible neighbour as 1. Otherwise, the cost is set to ∞.
2. From each accessible neighbour, it gets the costs to relay to other nodes via that neighbour (as the next hop).
3. Each node updates its routing table based on the information received in the previous two steps by choosing the minimum cost.

Continuing from the earlier problem, suppose at some time t, when the costs have stabilized, node A goes down. The cost from node F to node A at time (t + 100) is
>100 but finite | |
∞ | |
3 | |
>3 and ≤100 |
The distance between A and the nodes B, D, F respectively are:
t: 1 2 3
t + 1: 3 2 3
t + 2: 3 4 3
t + 3: 5 4 5
t + 4: 5 6 5
t + 5: 7 6 7
t + 6: 7 8 7
t + 7: 9 8 9
t + 8: 9 to 10
and this continues.
So, in every two steps they get incremented by 2.
So,
at t + 99, F is 101
at t + 100, F is 101.
Question 11 |
Which of the following is the correct decomposition of the directed graph given below into its strongly connected components?
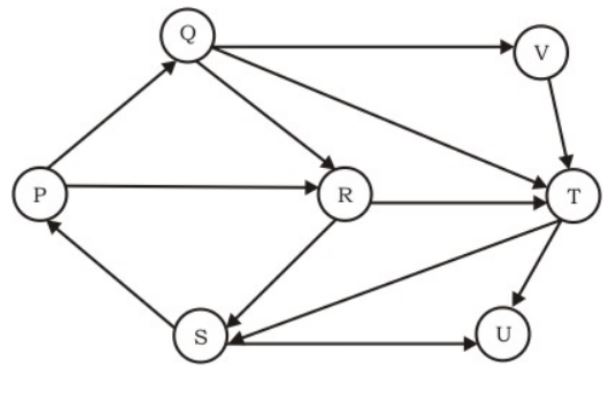
{P, Q, R, S}, {T}, {U}, {V} | |
{P, Q, R, S, T, V}, {U} | |
{P, Q, S, T, V}, {R}, {U} | |
{P, Q, R, S, T, U, V} |
From given graph {P, Q, R, S, T, V} and {U} are strongly connected components.
Question 12 |
Consider the depth-first-search of an undirected graph with 3 vertices P, Q, and R. Let discovery time d(u) represent the time instant when the vertex u is first visited, and finish time f(u) represent the time instant when the vertex u is last visited. Given that
d(P) = 5 units f(P) = 12 units d(Q) = 6 units f(Q) = 10 units d(R) = 14 unit f(R) = 18 units
Which one of the following statements is TRUE about the graph?
There is only one connected component | |
There are two connected components, and P and R are connected | |
There are two connected components, and Q and R are connected | |
There are two connected components, and P and Q are connected |
Question 13 |
A depth-first search is performed on a directed acyclic graph. Let d[u] denote the time at which vertex u is visited for the first time and f[u] the time at which the dfs call to the vertex u terminates. Which of the following statements is always true for all edges (u, v) in the graph?
d[u] < d[v] | |
d[u] < f[v] | |
f[u] < f[v] | |
f[u] > f[v] |

Option A:
d[u]
d[u]
f[u]
