Which of the following definitions below generates the same language as L, where L = {xⁿyⁿ such that n >= 1}?

 I. E → xEy|xy
 II. xy|(x+xyy+)
 III. x+y+ 

Let Σ = {0,1}, L = Σ* and R = {0ⁿ1ⁿ such that n >0} then the languages L ∪ R and R are respectively

Consider the following statements.

I. If L₁ ∪ L₂ is regular, then both L₁ and L₂ must be regular.
II. The class of regular languages is closed under infinite union.

Which of the above statements is/are TRUE?

If L is a regular language over Σ = {a,b}, which one of the following languages is NOT regular?

For Σ = {a,b}, let us consider the regular language L = {x|x = a^2+3k or x = b^10+12k, k ≥ 0}. Which one of the following can be a pumping length (the constant guaranteed by the pumping lemma) for L?

Which of the following statements is false?

(a) Given that A is regular and A∪B is regular, does it follow that B is necessarily regular? Justify your answer.
(b) Given two finite automata M1, M2, outline an algorithm to decide if L(M1)⊆L(M2). (note: strict subset)

Consider the following two statements:

S1: {0²ⁿ|n≥1|} is a regular language
S2: {0^m1ⁿ0^m+n|m≥1 and n≥1|} is a regular language

Which of the following statements is correct?

Consider the following languages:

L1 = {ww|w ∈ {a,b}*}
L2 = {ww^R|w ∈ {a,b}*, w^R is the reverse of w}
L3 = {0²ⁱ|i is an integer}
L3 = {0ⁱ²|i is an integer}

Which of the languages are regular?

• Consider the following two statements about regular languages:
  S₁: Every infinite regular language contains an undecidable language as a subset.
  S₂: Every finite language is regular.
  Which one of the following choices is correct.?

Let L be a regular language and M be a context-free language, both over the alphabet Σ. Let L^c and M^c denote the complements of L and M respectively. Which of the following statements about the language if L^c ∪ M^c is TRUE?

Which of the following statements is TRUE about the regular expression 01*0?

The language {0ⁿ 1ⁿ 2ⁿ | 1 ≤ n ≤ 10⁶} is

Consider the non-deterministic finite automaton (NFA) shown in the figure.

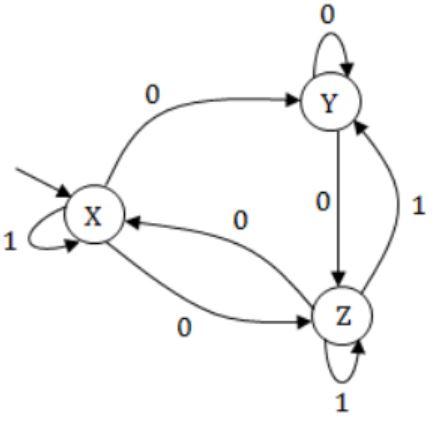
State X is the starting state of the automaton. Let the language accepted by the NFA with Y as the only accepting state be L1. Similarly, let the language accepted by the NFA with Z as the only accepting state be L2. Which of the following statements about L1 and L2 is TRUE? Correction in Question: There is an edge from Z->Y labeled 0 and another edge from Y->Z labeled 1 - in place of double arrowed and no arrowed edges.

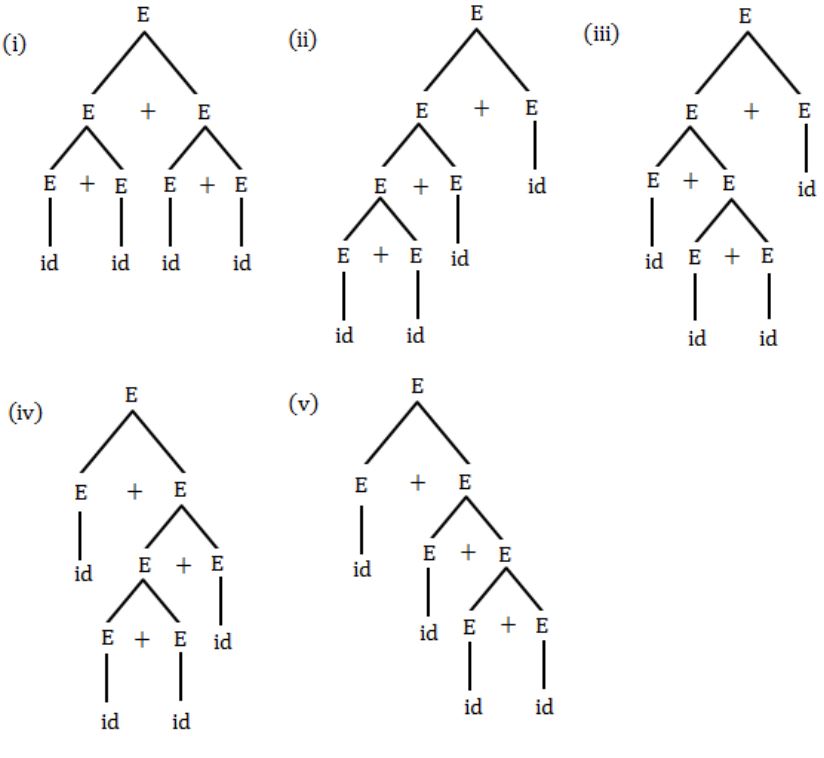
Consider the context-free grammar

E → E + E 
E → (E * E) 
E → id 

Which of the following statements about regular languages is NOT true?

Let L be a regular language. Consider the constructions on L below:
I. repeat (L) = {ww | w ∊ L}
II. prefix (L) = {u | ∃v : uv ∊ L}
III. suffix (L) = {v | ∃u : uv ∊ L}
IV. half (L) = {u | ∃v : | v | = | u | and uv ∊ L}
Which of the constructions could lead to a non-regular language?

Let L be a regular language. Consider the constructions on L below:
(I) repeat (L) = {ww | w ∊ L}
(II) prefix (L) = {u | ∃v : uv ∊ L}
(III) suffix (L) = {v | ∃u uv ∊ L}
(IV) half (L) = {u | ∃v : | v | = | u | and uv ∊ L}
Which choice of L is best suited to support your answer above?

Regularity is preserved under the operation of string reversal.

All subsets of regular sets are regular.