Boolean-Functions
Question 1 |
f(w, 0, 0, z) = 1
f(1, x, 1, z) = x + z
f(w, 1, y, z) = wz + y
The number of literals in the minimal sum-of-products expression of f is __________.
6 |
f(w,0,0,z)= 1 If x=y=0, then the sum of the corresponding minterms be 1.
The minterms with literals x’ and y’ are wx’y’z(9), w’x’y’z(1), wx’y’z’(8), w’x’y’z’(0) .
If x=y=0, then we get wz+w’z+wz’+w’z’ = 1.
f(1,x,1,z)= x+z.
The minterms with variables w and y in true form and x or z or both in true form.
The corresponding minterms are wx’yz(11), wxyz’(14), wxyz(15)
If w=1 and y=1, then we get x’z+xz’+xz= x+z.
f(w,1,y,z)= wz+y
The corresponding minterms are w’xyz’(6), w’xyz(7), wxyz’(14), wxyz(15), wxy’z(13).
If x=1, then we get w’yz’ + w’yz+ wyz’ + wyz+ wy’z = y + wz
So, the function f(w,x,y,z)= Σ(0,1,6,7, 8,9, 11, 13, 14, 15,).
Therefore, the k-map will be:
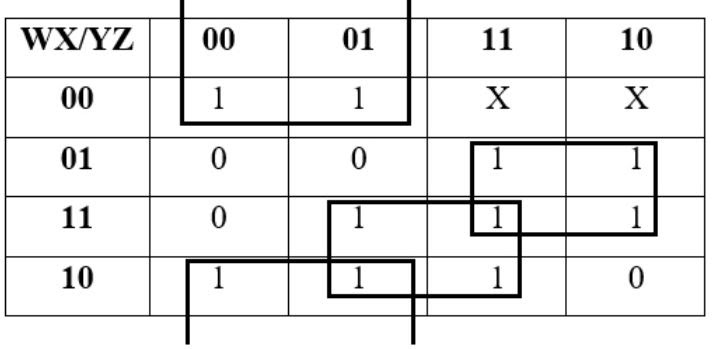
Therefore, the minimal expression will be: X’Y’ + WZ + XY
Thus, the number of literals will be 6.
Question 2 |
Which of the following sets of component(s) is/are sufficient to implement any arbitrary Boolean function?
XOR gates, NOT gates | |
2 to 1 multiplexors | |
AND gates, XOR gates | |
Three-input gates that output (A⋅B) + C for the inputs A⋅B and C | |
Both B and C |
(B) 2 to 1 multiplexors is functionally complete.
(C) XOR gate can be used to make a NOT gate. So, (AND, NOT) is functionally complete.
(D) With given gates and inputs NOT gate cannot be derived.
Hence, not complete.
Question 3 |

 | |
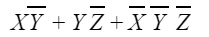 | |
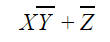 | |
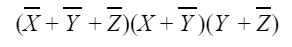 |

XY’+Z’ is a minimal SoP expression which represents the function (X,Y,Z).
The expression XY’ + YZ’ + X’Y’Z’ can be reduced to XY’+Z’
XY’ + YZ’ + X’Y’Z
= Y’(X+X’Z’) + YZ
= Y’(X+Z’) + Y
= XY’ + Y’Z’ + YZ’
= XY’ + (Y’+Y)Z’
= XY’ + Z’.
The expression (X+Z’)(Y’+Z’) is a PoS expression which also represents the same function (X,Y,Z).
Question 4 |
The majority function is a Boolean function f(x, y, z) that takes the value 1 whenever a majority of the variables x, y, z and 1. In the circuit diagram for the majority function shown below, the logic gates for the boxes labeled P and Q are, respectively,
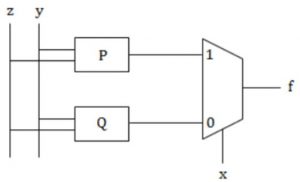
XOR, AND | |
XOR, XOR | |
OR, OR | |
OR, AND |
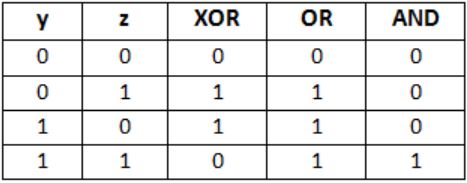
Thus we have OR and AND which gives different outputs on (0,0) and (1,1).
The encodes can be hence select from the two and decide output of the function according to x.
Question 5 |
The following expression was to be realized using 2-input AND and OR gates. However, during the fabrication all 2-input AND gates were mistakenly substituted by 2-input NAND gates.
(a.b).c + (a'.c).d + (b.c).d + a. dWhat is the function finally realized?
1 | |
a’ + b’ + c’ + d’ | |
a’ + b + c’ + d’ | |
a’ + b’ + c + d’ |
= ((ab)'c)' + ((a'c)'d)' + ((bc)'d)' + (ad)'
= ab + c' + a'c + d' + bc + d' + a' + d'
= ab + c' + a'c + bc + a' + d'
= ab + c' + bc + a' + d'
= b + c' + bc + a' + d'
= a' + b + c' + d'
Question 6 |
A set of Boolean connectives is functionally complete if all Boolean functions can be synthesized using those. Which of the following sets of connectives is NOT functionally complete?
EX-NOR | |
implication, negation | |
OR, negation | |
NAND |
→ NOR and NAND are the functionally complete logic gates, OR, AND, NOT only logic gate can be implemented by using them.
→ And (Implication, Negation) is also functionally complete.
Question 7 |
Consider the following Boolean function of four variables
f(A,B,C,D) = Σ(2, 3, 6, 7, 8, 9, 10, 11, 12, 13)The function is
independent of one variable | |
independent of two variables | |
independent of three variable | |
dependent on all the variables |
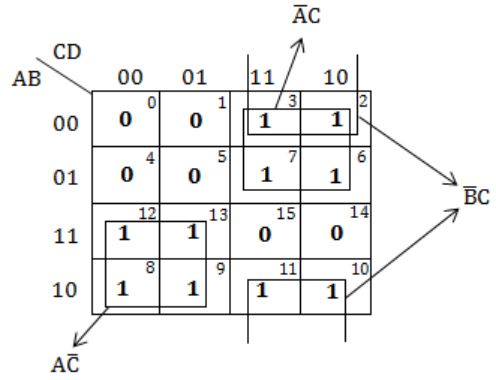
Independent of one variable '0'.
Question 8 |
The total number of Boolean functions which can be realized with four variables is:
4 | |
17 | |
256 | |
65,536 |
224 = 216 = 65,536
Question 9 |
n2 | |
2n2 | |
2n | |
2 to the power of 2n |
Number of variables= n
Number of input combinations is 2n.
Each “boolean” function has two possible outputs i.e 0 and 1.
Number of boolean functions possible is 22^n.
Formula: The number of m-ary functions possible with n k-ary variables is mk^n.
