Context-Free-Language
Question 1 |
Define for a context free language L ⊆ {0,1}*, init(L) = {u ∣ uv ∈ L for some v in {0,1}∗} (in other words, init(L) is the set of prefixes of L)
Let L = {w ∣ w is nonempty and has an equal number of 0’s and 1’s}
Then init(L) is
the set of all binary strings with unequal number of 0’s and 1’s | |
the set of all binary strings including the null string | |
the set of all binary strings with exactly one more 0’s than the number of 1’s or one more 1 than the number of 0’s | |
None of the above |
Question 2 |
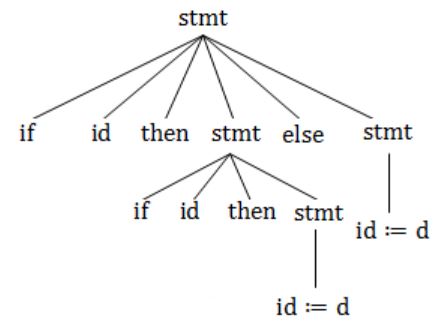
The grammar whose productions are
→ if id then → if id then else → id := id
is ambiguous because
the sentence if a then if b then c:=d | |
the left most and right most derivations of the sentence if a then if b then c:=d give rise top different parse trees | |
the sentence if a then if b then c:=d else c:=f has more than two parse trees | |
the sentence if a then if then c:=d else c:=f has two parse trees |
"if a then if b then c:=d else c:=f".
Parse tree 1:

Parse tree 2:
Question 3 |
Which one of the following languages over Σ = {a,b} is NOT context-free?
{wwR |w ∈ {a,b}*} | |
{wanwRbn |w ∈ {a,b}*, n ≥ 0} | |
{anbi | i ∈ {n, 3n, 5n}, n ≥ 0} | |
{wanbnwR |w ∈ {a,b}*, n ≥ 0} |
This is similar to language
L = {anbmcndm | n, m > 0}
Suppose we push “w” then an and then wR, now we cannot match bn with an, because in top of stack we have wR.
Question 4 |
Context-free languages are closed under:
Union, intersection | |
Union, Kleene closure | |
Intersection, complement | |
Complement, Kleene closure |
By checking the options only option B is correct.
Question 5 |
Show that the language L = {xcx| x ∈ {0,1}* and c is a terminal symbol} is not context free, c is not 0 or 1.
Theory Explanation. |
Question 6 |
I. {am bn cp dq ∣ m + p = n + q, where m, n, p, q ≥ 0}
II. {am bn cp dq ∣ m = n and p = q, where m, n, p, q ≥ 0}
III. {am bn cp dq ∣ m = n = p and p ≠ q, where m, n, p, q ≥ 0}
IV. {am bn cp dq ∣ mn = p + q, where m, n, p, q ≥ 0}
Which of the above languages are context-free?
I and IV only | |
I and II only | |
II and III only | |
II and IV only |
m-n = q-p
First we will push a’s in the stack then we will pop a’s after watching b’s.
Then some of a’s might left in the stack.
Now we will push c’s in the stack and then pop c’s by watching d’s.
And then the remaining a’s will be popped off the stack by watching some more d’s.
And if no d’s is remaining and the stack is empty then the language is accepted by CFG.
ii) am bn cp dq | m=n, p=q
Push a’s in stack. Pop a’s watching b’s.
Now push c’s in stack.
Pop c’s watching d’s.
So it is context free language.
iii) am bn cp dq | m=n=p & p≠q
Here three variables are dependent on each other. So not context free.
iv) Not context free because comparison in stack can’t be done through multiplication operation.
Question 7 |
L={w x wR xR | w, x ∈ {0,1}* } | |
L={w wR x xR | w, x ∈ {0,1}* } | |
L={w x xR wR | w, x ∈ {0,1}* } | |
L={w x wR | w, x ∈ {0,1}* } |
Option A: L={w x wR xR | w, x ∈ {0,1}* }
This is not CFL as if we push “w” then “x” then we cannot match wR with “w” as top of stack contains x.
Option B: L={w wR x xR | w, x ∈ {0,1}* }
This is CFL. We non deterministically guess the middle of the string. So we push “w” then match with wR and again push x and match with xR
Option C: L={w x xR wR | w, x ∈ {0,1}* }
This is also CFL. We non deterministically guess the middle of the string. So we push “w” then push x and then match with xR and again match with wR
Option D: L={w x wR | w, x ∈ {0,1}* }
This is a regular language (hence CFL). In this language every string start and end with same symbol (as x can expand).
Question 8 |
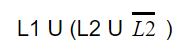 | |
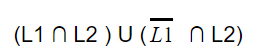 | |
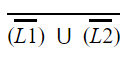 | |
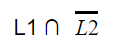 |

Question 9 |
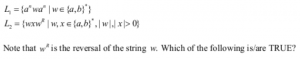
L 1 and L 2 are regular. | |
L 1 and L 2 are context-free. | |
L 1 is regular and L 2 is context-free. | |
L 1 and L 2 are context-free but not regular. |
Since no condition on the value of “n” is mentioned so for a particular case we can assume n=0, now when n=0 the language L1= w =(a+b)*
So if one case is (a+b)* then now even we assume any value of “n” the generated string will already present in (a+b)* thus L1=(a+b)*.
L2: In L2 the middle X can expand and consume all symbols of w except the first symbol and symbols of wr except the last symbol so L2 will be equivalent to language all strings start and end with the same symbol, hence L2 is regular.
Question 10 |

L 1 is not context-free but L 2 and L 3 are deterministic context-free. | |
Neither L 1 nor L 2 is context-free. | |
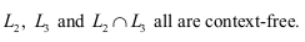 | |
Neither L 1 nor its complement is context-free. |
L2={an bn cm | m,n >=0} this contains only one comparison (number of a’s = number of b’s) so this is DCFL.
L3={am bn cn | m,n >=0} this contains only one comparison (number of b’s = number of c’s) so this is DCFL.
Intersection of L2 and L3 will have (number of a’s= number of b’s = number of c’s) i.e., {an bn cn | n >=0} so this is CSL (non-CFL).
So A is a true statement and rest all are false statements.
Question 11 |
The intersection of two CFL's is also a CFL.
True | |
False |
Question 12 |
Which of the following languages are context-free?
- L1 = {ambnanbm ⎪ m, n ≥ 1}
L2 = {ambnambn ⎪ m, n ≥ 1}
L3 = {ambn ⎪ m = 2n + 1}
L1 and L2 only | |
L1 and L3 only | |
L2 and L3 only | |
L3 only |
L2: First push all the a's in the stack then push all the b's in the stack. Now again a's come which cannot be compared by previous a's in the stack because at top of the stack's there are b's which is also needed to be pushed for further comparison with the next b's. So not CFL.
L3: First simply read one 'a', then push one 'a' in the stack after reading two a's and then pop all the a's by reading the b's. Since can be done by PDA hence CFL.
Question 13 |
L1 = {an bm cn+m: m,n ≥ 1}
L2= {an bn c2n: n ≥ 1}
Which one of the following is TRUE?
Both L1 and L2 are context-free. | |
L1 is context-free while L2 is not context-free. | |
L2 is context-free while L1 is not context-free. | |
Neither L1 nor L2 is context-free. |
At the end if input and stack is empty then accept.
Hence, it is CFL.
But L2 can’t be recognized by PDA, i.e. by using single stack.
The reason is, it has two comparison at a time,
1st comparison:
number of a’s = number of b’s
2nd comparison:
number of c’s must be two times number of a’s (or b’s)
It is CSL.
Question 14 |
Let L1, L2 be any two context-free languages and R be any regular language. Then which of the following is/are CORRECT?

I, II and IV only | |
I and III only | |
II and IV only | |
I only |
CFL is not closed under complementation.
So L1 compliment may or may not be CFL. Hence
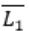 is Context free, is a false statement.
is Context free, is a false statement.L1 – R means
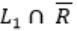 and Regular language is closed under compliment, so
and Regular language is closed under compliment, so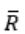 is also a regular language, so we have now L1 ∩ R .
is also a regular language, so we have now L1 ∩ R .Regular language is closed with intersection with any language, i.e. L∩R is same type as L.
So L1∩R is context free.
CFL is not closed under INTERSECTION, so L1 ∩ L2 may or may not be CFL and hence IVth is false.
Question 15 |
L1= {ap│p is a prime number}
L2= {anbmc2m| n ≥ 0, m ≥ 0}
L3= {anbnc2n│ n ≥ 0}
L4= {anbn│ n ≥ 1}
Which of the following are CORRECT?
I. L1 is context-free but not regular.
II. L2 is not context-free.
III. L3 is not context-free but recursive.
IV. L4 is deterministic context-free.
I, II and IV only | |
II and III only | |
I and IV only | |
III and IV only |
L2 = {an bm c2m│n ≥ 0, m ≥ 0} is a context free as we have to do only one comparison (between b’s and c’s) which can be done by using PDA, so L2 is Context free and II is true.
L3 = {an bn c2n│n≥0} is context sensitive.
The reason it has more than one comparison (at a time) as we have to compare number of a’s, b’s and c’s.
So this cannot be done using PDA. Hence III is CSL and every CSL is recursive, so III is True
L4 = {an bn│n ≥ 1} is Context free (as well as Deterministic context free).
We can define the transition of PDA in a deterministic manner.
In beginning push all a’s in stack and when b’s comes pop one “a” for one “b”.
If input and stack both are empty then accept.
