Finite-Automata
Question 1 |
Consider the following language.
L = {x ∈ {a,b}* | number of a’s in x is divisible by 2 but not divisible by 3}
The minimum number of states in a DFA that accepts L is ______.
6 |
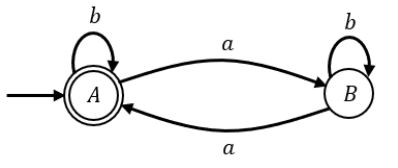
DFA 1: No. of a’s not divisible by 3
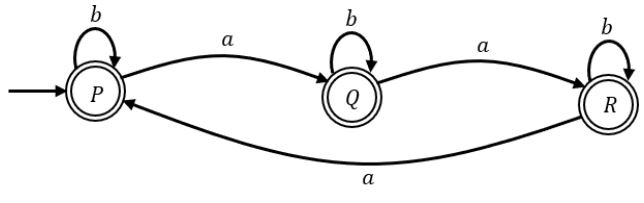
Using product automata:

Question 2 |
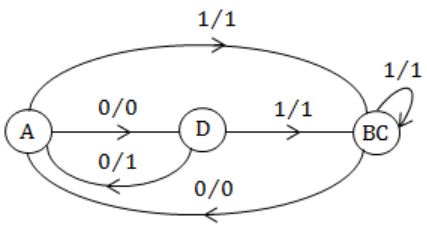
Consider the given figure of state table for a sequential machine. The number of states in the minimized machine will be
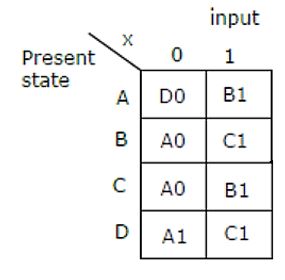
4 | |
3 | |
2 | |
1 |
Question 3 |
Let N be an NFA with n states. Let k be the number of states of a minimal DFA which is equivalent to N. Which one of the following is necessarily true?
k ≥ 2n | |
k ≥ n | |
k ≤ n2 | |
k ≤ 2n
|
In other words, if number of states in NFA is “n” then the corresponding DFA have at most 2n states.
Hence k ≤ 2n is necessarily true.
Question 4 |
L0 = {ε}
Li = Li-1∙L for all i>0
The order of a language L is defined as the smallest k such that Lk = Lk+1.
Consider the language L1 (over alphabet 0) accepted by the following automaton.
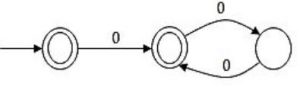
The order of L1 is ______.
2 | |
3 | |
4 | |
5 |
Now L10 = ϵ and L11 = ϵ . (ϵ+0 (00)*) = ϵ + 0 (00)* = L1
Now L12 = L11 .
L1 = L1 .
L1 = (ϵ + 0 (00)*) (ϵ + 0 (00)*)
= (ϵ + 0 (00)* + 0(00)* + 0(00)*0(00)*)
= (ϵ + 0 (00)* + 0(00)*0(00)* ) = 0*
As it will contain epsilon + odd number of zero + even number of zero, hence it is 0*
Now L13 = L12 .
L1 = 0* (ϵ + 0 (00)*) = 0* + 0*0(00)* = 0*
Hence L12 = L13
Or L12 = L12+1 ,
hence the smallest k value is 2.
Question 5 |
Both A and B are equal, which generates strings over {0,1}, while 0 is followed by 1.
The numbers 1, 2, 4, 8, ……………., 2n, ………… written in binary | |
The numbers 1, 2, 4, ………………., 2n, …………..written in unary | |
The set of binary string in which the number of zeros is the same as the number of ones | |
The set {1, 101, 11011, 1110111, ………..} |
10, 100, 1000, 10000 .... = 10*
which is regular and recognized by deterministic finite automata.
Question 6 |
Let L be the set of all binary strings whose last two symbols are the same. The number of states in the minimum state deterministic finite 0 state automaton accepting L is
2 | |
5 | |
8 | |
3 |

Equivalent DFA:
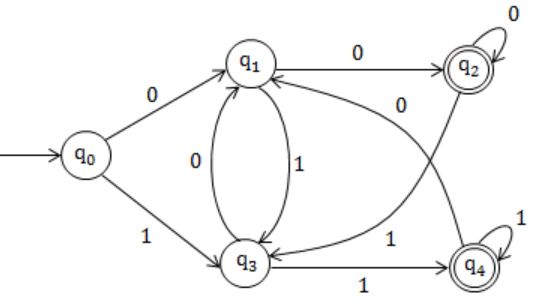
Hence, 5 states.
Question 7 |
Consider the regular expression (0 + 1) (0 + 1)…. N times. The minimum state finite automation that recognizes the language represented by this regular expression contains
n states | |
n + 1 states | |
n + 2 states | |
None of the above |
DFA:

So, DFA requires (n+2) state.
NFA:

So, NFA requires (n+1) state.
So, final answer will be,
min(n+1, n+2)
= n+1
Question 8 |
What can be said about a regular language L over {a} whose minimal finite state automation has two states?
L must be {an |n is odd} | |
L must be {an |n is even} | |
L must be {an|≥0} | |
Either L must be {an |n is odd}, or L must be {an | n is even} |
Question 9 |
Given an arbitrary non-deterministic finite automaton (NFA) with N states, the maximum number of states in an equivalent minimized DFA is at least
N2 | |
2N | |
2N | |
N! |
If NFA have two states {1}{2} = 2
Then DFA may contain {ϕ}{1}{2}{1,2} = 4 = 22 = 2N
Question 10 |
Consider a DFA over Σ = {a,b} accepting all strings which have number of a's divisible by 6 and number of b's divisible by 8. What is the minimum number of states that the DFA will have?
8 | |
14 | |
15 | |
48 |
Same as b's divisible by 8 contains 8 state.
Total no. of states is = 8 * 6 = 48
Question 11 |
Construct DFA’s for the following languages:
(a) L = {w|w ∈ {a,b}*, w has baab as a subsring }
(b) L = {w|w ∈ {a,b}*, w has an odd number of a's and an odd number of b's} Theory Explanation is given below. |
Question 12 |
The Finite state machine described by the following state diagram with A as starting state, where an arc label is x/y and x stands for 1-bit input and y stands for 2- bit output
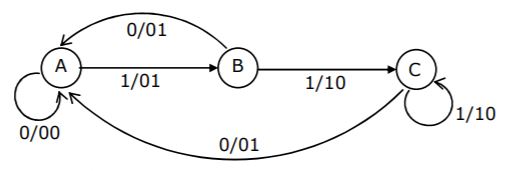
Outputs the sum of the present and the previous bits of the input. | |
Outputs 01 whenever the input sequence contains 11 | |
Outputs 00 whenever the input sequence contains 10 | |
None of the above |
(A,1) = (B, 01)
Previous input + Present input = 0+1 = 01
(B,0) = (A, 01)
Previous input + Present input = 1+0 = 01
(A,0) = (A, 00)
Previous input + Present input = 0+0 = 00
(A,1) = (B, 01)
Previous input + Present input = 0+1 = 01
(B,1) = (C, 10)
Previous input + Present input = 1+1 = 10
(C,1) = (C, 10)
Previous input + Present input = 1+1 = 10
Question 13 |
The smallest finite automaton which accepts the language {x|length of x is divisible by 3} has
2 states | |
3 states | |
4 states | |
5 states |
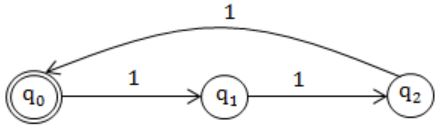
Minimum no. of states that we require is "3".
Question 14 |
We require a four state automaton to recognize the regular expression (a|b)*abb.
- (a) Give an NFA for this purpose.
(b) Give a DFA for this purpose.
Theory Explanation is given below. |
Question 15 |
Consider the following deterministic finite state automaton M.

Let S denote the set of seven bit binary strings in which the first, the fourth, and the last bits are 1. The number of strings in S that are accepted by M is
1 | |
5 | |
7 | |
8 |

There are possible: 7 strings.
Question 16 |
Consider the NFA M shown below.
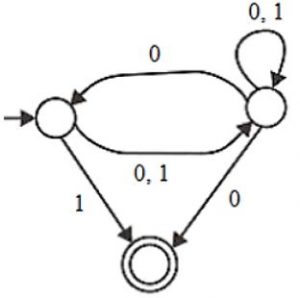
Let the language accepted by M be L. Let L1 be the language accepted by the NFA M1, obtained by changing the accepting state of M to a non-accepting state and by changing the non-accepting state of M to accepting states. Which of the following statements is true?
L1 = {0,1}* - L | |
L1 = {0,1}* | |
L1 ⊆ L | |
L1 = L |
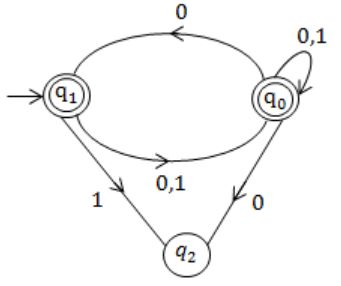
As in above NFA language,
L1 is {0,1}*.
Question 17 |
The following finite state machine accepts all those binary strings in which the number of 1's and 0's are respectively.

divisible by 3 and 2 | |
odd and even | |
even and odd | |
divisible by 2 and 3 |
For example 001 consists of even no. of zero's and odd no. of one's. It is not accepted by TM.
So, it is false.
Option C:
For example 110, contains even 1's and odd 0's but not accepted by TM.
So, it is false.
Option D:
For example 11000, where no. of 1's divisible by '2', and no. of zero's divisible by 3, but not accepted by TM.
So, it is false.
Option A:
It accepts all string where no. of 1's divisible by 3, and no. of zero's divisible by 2.
It is true.
Question 18 |
The regular expression for the language recognized by the finite state automaton of figure is __________
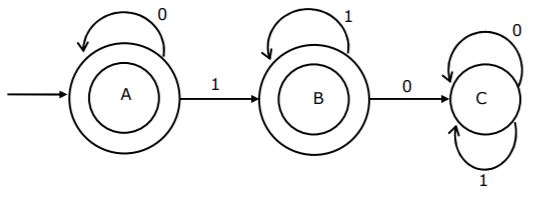
L = 0*1* |
L contains all binary strings where a 1 is not followed by a 0.
Question 19 |
If the state machine described in figure, should have a stable state, the restriction on the inputs is given by

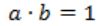 | |
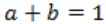 | |
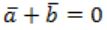 | |
 |
Question 20 |
Which of the following three statements are true? Prove your answer.
- (i) The union of two recursive languages is recursive.
(ii) The language {O"|n is a prime} is not regular.
(iii) Regular languages are closed under infinite union.
Theory Explanation. |
Question 21 |
Let M = {K,Σ,δ,s,F} be a finite state automaton, where
K = {A,B}, Σ = {a,b}, s = A, F = {B}, δ(A,a) = A, δ(A,b) = B, δ(B,a) = B and δ(B,a) = A
A grammar to generate the language accepts by M can be specified as G = (V,Σ,R,S), where V = K∪Σ, and S = A.
Which one of the following set to rules will make L(G) = L(M)?
{A→aB, A→bA, B→bA, B→aA, B→ε} | |
{A→aA, A→bB, B→bB, B→aA, B→ε} | |
{A→bB, A→aB, B→aA, B→bA, A→ε} | |
{A→aA, A→bA, B→bB, B→aA, A→ε} |
Question 22 |
In the automaton below, s is the start state and t is the only final state.

Consider the strings u = abbaba, v = bab, and w = aabb. Which of the following statements is true?
The automaton accepts u and v but not w | |
The automaton accepts each of u, v, and w | |
The automaton rejects each of u, v, and w | |
The automaton accepts u but rejects v and w |
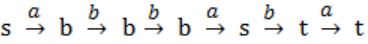
where t is final state
(ii) v = bab
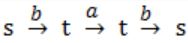
s is not final state
(iii) w = aabb
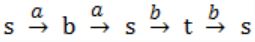
s is not final state
Question 23 |
For a state machine with the following state diagram the expression for the next state S+ in terms of the current state S and the input variables x and y is

S+ = S’ . y’ + S . x | |
S+ = S. x . y’ + S’ . y . x’ | |
S+ = x . y’ | |
S+ = S’ . y + S . x’col |

From the table:
S' = S'y' + Sx
