Functional-Dependency

Question 1

Let R = (A, B, C, D, E, F) be a relation scheme with the following dependencies: C→F, E→A, EC→D, A→B. Which of the following is a key of R?

A
CD
B
EC
C
AE
D
AC
Database-Management-SystemFunctional-DependencyGATE 1999
Question 1 Explanation: 
Let's check closure for each option,
A) (CD)+ = cdf
Not a key.
B) (EC)+ = ecdabf
Yes, it is a key.
C) (AE)+ = aeb
Not a key. D) (AC)+ = abcf
Not a key.
Question 2

Given the following relation instance.

          x  y  z
          1  4  2
          1  5  3
          1  6  3
          3  2  2

Which of the following functional dependencies are satisfied by the instance?

A
XY → Z and Z → Y
B
YZ → X and Y → Z
C
YZ → X and X → Z
D
XZ → Y and Y → X
Database-Management-SystemFunctional-DependencyGATE 2000
Question 2 Explanation: 
A functional dependency A→B is said to hold if for two tuples t1 and t2.
If for t1[A] = t2[A] then t1[Y] = t2[Y].
Question 3

Consider a schema R(A,B,C,D) and functional dependencies A → B and C → D. Then the decomposition of R into R1(AB) and R2(CD) is

A
dependency preserving and lossless join
B
lossless join but not dependency preserving
C
dependency preserving but not lossless join
D
not dependency preserving and not lossless join
Database-Management-SystemFunctional-DependencyGATE 2001
Question 3 Explanation: 
If the given relations are to be lossless then
R1∩R2 ≠ 0
Given R1(A,B), R2
R1∩R2 = 0
Not lossless.
The given relation decomposed into R1(A,B) and R2(C,D) and there are only two functional dependencies A→B and C→D. So the given decomposition is dependency preserving.
Question 4

From the following instance of a relation scheme R(A,B,C), we can conclude that:

A
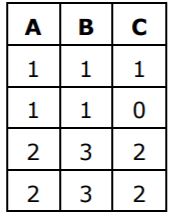
A functionally determines B and B functionally determines C
B
A functionally determines B and B does not functionally determines C
C
B does not functionally determines C
D
A does not functionally determines B and B does not functionally determines C
Database-Management-SystemFunctional-DependencyGATE 2002
Question 4 Explanation: 
From the given instance of relation it can be seen that A functionally determines B, but we cannot conclude this for the entire relation.
But for the given instance it can be seen that B does not functionally determines C, and it can be concluded for entire relation.
Question 5
 Suppose the following functional dependencies hold on a relation U with attributes P, Q, R, S, and T:
                  P⟶ QR
                  RS⟶ T 
Which of the following functional dependencies can be inferred from the above functional dependencies?
A
PS ⟶ Q
B
PS ⟶ T
C
R ⟶ T
D
P ⟶ R
Database-Management-SystemFunctional-DependencyGATE 2021 CS-Set-2Video-Explanation
Question 5 Explanation: 
Question 6
Consider a relation R ( A , B , C , D , E ) with the following three functional dependencies.
AB → C; BC → D; C → E;
The number of superkeys in the relation R is _____________.
A
8
Database-Management-SystemFunctional-DependencyGATE 2022Video-Explanation
Question 6 Explanation: 
R(A, B, C, D, E)
AB → C
BC → D
C → E
¯ The attributes A, B are not there in the right hand side of any of the given FDs.
¯ So, AB can be a candidate key.
(AB)^+ = ABCDE
¯ (AB)^+ is deriving all the attributes of R Hence, AB is a candidate key.
¯ The number of super keys possible for R with “AB” candidate kay is:
2^5 – 2 = 2^3
= 8
Question 7

Consider a relation R with five attributes V, W, X, Y, and Z. The following functional dependencies hold: VY → W, WX → Z, and ZY → V.
Which of the following is a candidate key for R?

A
VXZ
B
VXY
C
VWXY
D
VWXYZ
Database-Management-SystemFunctional-DependencyGATE 2006-IT
Question 7 Explanation: 
As we can see that attribute XY do not appear in RHS of an FD, they need to be a part of key.
Candidate keys are
VXY, WXY, ZXY
Question 8

Let R (A, B, C, D) be a relational schema with the following functional dependencies: A → B, B → C, C → D and D → B.

The decomposition of R into (A, B), (B, C), (B, D)

A
gives a lossless join, and is dependency preserving
B
gives a lossless join, but is not dependency preserving
C
does not give a lossless join, but is dependency preserving
D
does not give a lossless join and is not dependency preserving
Database-Management-SystemFunctional-DependencyGATE 2008-IT
Question 8 Explanation: 
(A, B) (B, C) - common attribute is (B) and due to B→C, B is a key for (B, C) and hence ABC can be losslessly decomposed into (A, B)and (B, C).
(A, B, C) (B, D) - common attributes is B and B→D is a FD (via B→C, C→D), and hence, B is a key for (B, D). So, decomposition of (A, B, C, D) into (A, B, C) (B, D) is lossless.
Thus the given decomposition is lossless.
The given decomposition is also dependency preserving as the dependencies A→B is present in (A, B), B→C is present in (B, C), D→B is present in (B, D) and C→D is indirectly present via C→B in (B, C) and B→D in (B, D).
Question 9

Consider the relation X(P, Q, R, S, T, U) with the following set of functional dependencies

F = {
       {P, R} → {S,T},  
       {P, S, U} → {Q, R}
    }

Which of the following is the trivial functional dependency in F+ is closure of F?

A
{P,R}→{S,T}
B
{P,R}→{R,T}
C
{P,S}→{S}
D
{P,S,U}→{Q}
Database-Management-SystemFunctional-DependencyGATE 2015 [Set-3]Video-Explanation
Question 9 Explanation: 
X→Y is trivial if Y⊆ X
Question 10
The symbol → indicates functional dependency in the context of a relational database. Which of the following options is/are TRUE?
A
(X,Y)→ (Z,W) implies X→ (Z,W)
B
(X,Y)→ (Z,W) implies (X,Y)→ Z
C
((X,Y)→ Z and W→ Y) implies (X,W)→ Z
D
(X→Yand Y→ Z) implies X→ Z
database-management-systemFunctional-DependencyGATE-2024-CS1(Forenoon)
Question 10 Explanation: 
(A) (X,Y) → (Z,W) implies X → (Z,W) This statement is not necessarily true. The functional dependency (X,Y) → (Z,W) means that for any given value of X and Y, there is a unique value of Z and W. However, this does not imply that for any given value of X, there is a unique value of Z and W. So, option (A) is FALSE. (B) (X,Y) → (Z,W) implies (X,Y) → Z This statement is TRUE. If (X,Y) functionally determines (Z,W), then it also functionally determines Z. This is because for any given combination of X and Y, there is a unique value of Z according to the functional dependency. So, option (B) is TRUE. (C) ((X,Y) → Z and W → Y) implies (X,W) → Z This statement is TRUE. If X and Y together determine Z and W determines Y, then X and W together determine Z. This is because for any given combination of X and W, we can find the corresponding values of Y and then use (X,Y) → Z to determine the value of Z. So, option (C) is TRUE. (D) (X → Y and Y → Z) implies X → Z This statement is TRUE. If X determines Y and Y determines Z, then X determines Z. This is because the transitive property of functional dependency applies here. So, option (D) is TRUE
Question 11
The following functional dependencies hold true for the relational schema {V, W, X, Y, Z} :
V → W
VW → X
Y → VX
Y → Z
Which of the following is irreducible equivalent for this set of functional dependencies?
A
V→W
V→X
Y→V
Y→Z
B
V→W
W→X
Y→V
Y→Z
C
V→W
V→X
Y→V
Y→X
Y→Z
D
V→W
W→X
Y→V
Y→X
Y→Z
Database-Management-SystemFunctional-DependencyGATE 2017 [Set-1]Video-Explanation
Question 11 Explanation: 
Step 1:
V → W, VW → X, Y → V, Y → X, Y→ Z
Step 2:
V → W, VW → X, Y → V, Y → X, Y→ Z
(V)+ = V ×
(VW)+ = VW ×
(Y)+ = YXZ
(Y)+ = YVW ×
(Y)+ = YVWX
Without Y → X, the closure of Y is deriving ‘X’ from the remaining attributes.
So, we can remove Y → X as its redundant.
Step 3:
V → W, VW → X, Y → V, Y → Z
(V)+ = VW, the closure of V is deriving W from the remaining FD’s.
So, W is redundant. We can remove it.
So, the final canonical form is
V→W, V→X, Y→V, Y→Z
⇾ So, option (A) is correct.
Question 12

Consider the relation scheme R = (E, F, G, H, I, J, K, L, M, N) and the set of functional dependencies  {{E,F} → {G}, {F} → {I,J}, {E,H} → {K,L}, {K} → {M}, {L} → {N}} on R. What is the key for R?

A
{E,F}
B
{E,F,H}
C
{E,F,H,K,L}
D
{E}
Database-Management-SystemFunctional-DependencyGATE 2014 [Set-1]Video-Explanation
Question 12 Explanation: 
A) (EF)+ = EFGIJ. So, EF is not a key.
B) (EFH)+ = EFHGIJKLMN, EFH is deriving all the attributes of R. So, EFH is a key.
C) If EFH is a key, then EFHKL will become the super key.
D) (E)+ = E
Question 13

The following functional dependencies are given:

  AB → CD, AF → D, DE → F, C → G, F → E, G → A.

Which one of the following options is false?

A
{CF}+ = {ACDEFG}
B
{BG}+ = {ABCDG}
C
{AF}+ = {ACDEFG}
D
{AB}+ = {ABCDFG}
Database-Management-SystemFunctional-DependencyGATE 2006
Question 13 Explanation: 
AB → CD
AF → D
DE → F
C → G
F → E
G → A
CF+ = {G,E,A,D,C,F} = {A,C,D,E,F,G} (✔️)
BG+ = {B,G,A,C,D} = {A,B,C,D,G} (✔️)
AF+ = {D,E,A,F} = {A,D,E,F} (❌)
AB+ = {A,B,C,D,G} (❌)
Question 14

Consider a relation scheme R = (A, B, C, D, E, H) on which the following functional dependencies hold: {A → B, BC → D, E → C, D → A}. What are the candidate keys of R?

A
AE, BE
B
AE, BE, DE
C
AEH, BEH, BCH
D
AEH, BEH, DEH
Database-Management-SystemFunctional-DependencyGATE 2005
Question 14 Explanation: 
Using the given functional dependencies and looking at the dependent attributes, E and H are not dependent on any. So, they must be a part of any candidate key.
So only option (D) contains E and H as part of candidate key.
Question 15
The 9’s compliment of the decimal number 139452 is:
A
971658
B
971659
C
860547
D
860548
Database-Management-SystemFunctional-DependencyCIL Part - B
Question 15 Explanation: 
→To obtain the 9’s complement of any number we have to subtract the number with (10n – 1) where n = number of digits in the number, or in a simpler manner we have to divide each digit of the given decimal number with 9
→Subtract each and every digit of given number by digit “9”.
999999
139452
________
860547
Question 16
If D={R1,R2} is a decomposition of R, and F is the set of functional dependencies on R, then which of the following ensures that the decomposition D is lossless (nonadditive)?
A
((R1∩ R2) →(R1-R2)) ∈ F+
B
((R1 ∩R2) → (R1 - R2)) ∉ F+
C
((R1 ∪ R2) →(R1 - R2)) ∈ F+
D
((R1∩R2) →R1 ) ∈ F+
Database-Management-SystemFunctional-DependencyCIL Part - B
Question 16 Explanation: 
Question 17
Consider the relation R shown in the below Figure.
X Y Z
X1 Y1 Z1
X1 Y1 Z2
X2 Y1 Z1
X2 Y1 Z3
  List all the functional dependencies that this relation instance satisfies.
A
R: Z → Y, X → Y, and X → Z
B
R: Z →Y, X → Y, and XZ → Y
C
R: X →Y, X → Z, and XZ → Y
D
R: Z →Y, X → Z, and XZ → Y
Database-Management-SystemFunctional-DependencyAPPSC-2016-DL-CS
Question 17 Explanation: 
option 1 is wrong bacause X → Z does not satisfy, since X1 is mapped to two values Z1 and Z2.
Option 3 is wrong because of X → Z.
Option 4 is wrong because of X → Z
Question 18
Consider the table R with attributes A, B and C. The functional dependencies that hold on R are : A → B, C → AB. Which of the following statements is/are True ?
I. The decomposition of R into R1(C, A) and R2(A, B) is lossless.
II. The decomposition of R into R1(A, B) and R2(B, C) is lossy.
A
Only I
B
Only II
C
Both I and II
D
Neither I nor II
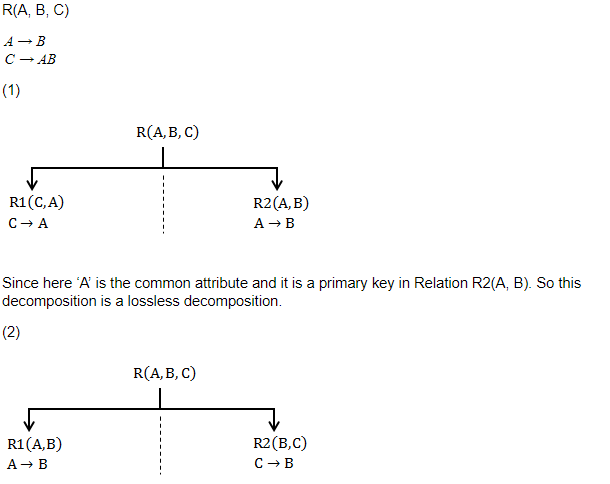
Database-Management-SystemFunctional-DependencyUGC NET CS 2016 Aug- paper-3
Question 18 Explanation: 

Here ‘B’ is common attribute but ‘B’ is not the primary key in any of the decomposed relations (R1 or R2). Hence this decomposition is not a lossless decomposition i.e., it is a lossy decomposition.
Hence, option (C) is correct.
Question 19
Consider a Relational schema R(A, B, C, D) and functional dependencies A → B and C → D. Then the decomposition of R into R1 (A, B) and R2(C, D) is
A
dependency preserving and lossless join
B
lossless join but not dependency preserving
C
dependency preserving but not lossless join
D
neither dependency·preserving nor lossless join
Database-Management-SystemFunctional-DependencyHCU PHD CS MAY 2019
Question 19 Explanation: 
R1(A,B) contains FD A→B
R2(C,D) contains FD C→D
So, yes dependency preserving.
But there is no common attribute between R1 and R2, hence not lossless join.
There are 19 questions to complete.

Access quiz wise question and answers by becoming as a solutions adda PRO SUBSCRIBER with Ad-Free content

If you have registered and made your payment please contact solutionsadda.in@gmail.com to get access