Functions
Question 1 |
Consider the following C functions.
int fun1 (int n) { int fun2 (int n) {
static int i = 0; static int i = 0;
if (n > 0) { if (n > 0) {
++i; i = i + fun1 (n);
fun1 (n-1); fun2 (n-1);
} }
return (i); return (i);
} }
The return value of fun2 (5) is _______.
55 |
int fun1(int n) {
printf("--fun1 call--\n");
static int i = 0;
if(n>0){
++i;
printf("fun1(%d-1)\n",n);
fun1(n-1);
}
printf("fun1(%d)= %d\n",n, i);
return(i);
}
int fun2(int n) {
printf("\n******* fun2 call ********\n");
static int i = 0;
if(n>0){
printf("%d + fun1(%d)\n", i,n);
i=i+fun1(n);
fun2(n-1);
}
printf("fun2(%d)= %d\n",n, i);
return(i);
}
void main()
{
printf("final = %d\n", fun2(5));
}
Check step by step hand run of the code to understand the recursion:
******* fun2 call ********
0 + fun1(5)
--fun1 call--
fun1(5-1)
--fun1 call--
fun1(4-1)
--fun1 call--
fun1(3-1)
--fun1 call--
fun1(2-1)
--fun1 call--
fun1(1-1)
--fun1 call--
fun1(0)= 5
fun1(1)= 5
fun1(2)= 5
fun1(3)= 5
fun1(4)= 5
fun1(5)= 5
******* fun2 call ********
5 + fun1(4)
--fun1 call--
fun1(4-1)
--fun1 call--
fun1(3-1)
--fun1 call--
fun1(2-1)
--fun1 call--
fun1(1-1)
--fun1 call--
fun1(0)= 9
fun1(1)= 9
fun1(2)= 9
fun1(3)= 9
fun1(4)= 9
******* fun2 call ********
14 + fun1(3)
--fun1 call--
fun1(3-1)
--fun1 call--
fun1(2-1)
--fun1 call--
fun1(1-1)
--fun1 call--
fun1(0)= 12
fun1(1)= 12
fun1(2)= 12
fun1(3)= 12
******* fun2 call ********
26 + fun1(2)
--fun1 call--
fun1(2-1)
--fun1 call--
fun1(1-1)
--fun1 call--
fun1(0)= 14
fun1(1)= 14
fun1(2)= 14
******* fun2 call ********
40 + fun1(1)
--fun1 call--
fun1(1-1)
--fun1 call--
fun1(0)= 15
fun1(1)= 15
******* fun2 call ********
fun2(0)= 55
fun2(1)= 55
fun2(2)= 55
fun2(3)= 55
fun2(4)= 55
fun2(5)= 55
final = 55
Question 2 |
int tob (int b, int* arr) {
int i;
for (i=0; b>0; i++) {
if (b%2) arr [i] = 1;
else arr [i] = 0;
b = b/2;
}
return (i);
}
int pp (int a, int b) {
int arr [20];
int i, tot = 1, ex, len;
ex = a;
len = tob (b,arr);
for (i=0; i
tot = tot * ex;
ex = ex * ex;
}
return (tot);
}
The value returned by pp(3,4) is ________.
81 |
a=3,b=4
tot=1
ex=a=3
len=tob(b,arr) which is 3
[
tob(4,arr)==>
b=4
b%2 =4%2=0 Condition is false then arr[0]=0
=> b=b/2 =4/2 =2
b=2
b%2 =2%2=0 condition is false then arr[1]=0
=>b=b/2=2/2=1
b=1
then b%2=1%2 condition is true then arr[2]=1
=>b=b/2=1/2=0
The i value is 3 [length is 3]
]
i=0,
arr[0] ==1 condition is false
ex=3*3=9
i=1
arr[1]==1 condition is false
then
ex=9*9=81
i=2
then arr[2]==1 condition is true
tot=tot*ex=1*81=81
ex=81*81
Finally it returns tot value which 81.
Question 3 |
Let A be a set of n(>0) elements. Let Nr be the number of binary relations on A and let Nf be the number of functions from A to A.
- (a) Give the expression for Nr in terms of n.
(b) Give the expression for Nf in terms of n.
(c) Which is larger for all possible n, Nr or Nf?
Theory Explanation is given below. |
Question 4 |
On the set N of non-negative integers, the binary operation __________ is associative and non-commutative.
fog |
(fog)(x) = f(g(x))
It is associative, (fog)oh = fo(goh), but its usually not commutative. fog is usually not equal to gof.
Note that if fog exists then gof might not even exists.
Question 5 |
What function of x, n is computed by this program?
Function what (x, n:integer): integer:
Var
value : integer;
begin
value:=1
if n>0 then
begin
if n mod 2 = 1 then
value:=value*x;
value:=value*what(x*x, n div 2);
end;
what:value
end; Theory Explanation. |
Question 6 |
(a) Draw a precedence graph for the following sequential code. The statements are numbered from S1 to S6
S1 read n S2 i:=1 S3 if i>n goto next S4 a(i):=i+1 S5 i:=i+1 S6 next : Write a(i)
(b) Can this graph be converted to a concurrent program using parbegin-parend construct only?
Theory Explanation. |
Question 7 |
The function f(x,y) = x2y - 3xy + 2y + x has
no local extremum | |
one local minimum but no local maximum | |
one local maximum but no local minimum | |
one local minimum and one local maximum |
Question 8 |
The Laplace transform of the periodic function f(t) described by the curve below, i.e.,
is _________
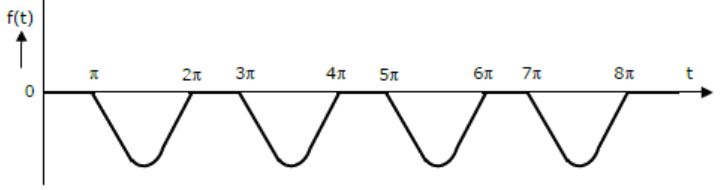
Out of syllabus. |
Question 9 |
Let A and B be sets with cardinalities m and n respectively. The number of one-one mappings (injections) from A to B, when m < n, is:
mn | |
nPm | |
mCn | |
nCm | |
mPn |
A = {a1, a2, ... am} and
B = {b1, b2, ... bn}
A one-one function 'f' assigns each element ai of A a distinct element, bj=f(ai) of Bi for a, there are n choices, for a2 there are n-1 choices, for am there are (n-(m-1)) choices.
i.e.,

Question 10 |
int SimpleFunction (int Y[], int n, int x)
{
int total = Y[0], loopIndex;
for (loopIndex = 1; loopIndex <= n - 1; loopIndex++)
total = x * total + Y[loopIndex]
return total;
}
Let Z be an array of 10 elements with Z[i]=1, for all i such that 0 ≤ i ≤ 9. The value returned by SimpleFunction(Z, 10, 2) is _______
1023 |
n=10,x=2
Initial total value is 1 => total=1.
For loop will execute 9 times.
loopindex=1, 1<=9 condition is true then
total = x * total + Y[loopIndex]= 2*1+Y[1]=2+1=3
loopindex=2, 2<=9 condition is true then
total=2*3+Y[2]=6+1=7
loopindex=3, 3<=9 condition is true then
total=2*7+Y[3]=14+1 =15
loopindex=4, 4<=9 condition is true then
total= 2*15+Y[4]=30+1=31
loopindex=5, 5<=9 condition is true then
total=2*31+Y[5]=62+1=63
loopindex=6, 6<=9 condition is true then
total=2*63+Y[6]=126+1=127
loopindex=7, 7<=9 condition is true then
Total =2*127+Y[7]=254+1=255
loopindex=8, 8<=9 condition is true then
total=2*255+Y[8]=510+1=511
loopindex=9, 9<=9 condition is true then
total=2*511+Y[9]=1022+1=1023
loopindex=10, 10<=9 condition is false then
Total value is returned which is 1023.
You can also write generalized formulae 210-1=1023
Question 11 |
#include
int funcp(){
static int x = 1;
x++;
return x;
} int main(){ int x,y;
x = funcp();
y = funcp()+x;
printf("%d\n", (x+y));
return 0;
}
7 |
static int x = 1; // here “x” is a static variable and the updated value will be carried for all remaining function calls.
x++;
return x; // incremented value will be returned to calling function
}
int main(){
int x,y;
x = funcp(); // funcp() will return the value “2” and value “2” will stored in the variable “x”
y = funcp()+x; //funcp() will return the value “3” and it will be added to “2” and value “5” be stored in the variable “y”
printf("%d\n", (x+y)); // 2+5 =7 value will be displayed
return 0;
}
Question 12 |
Consider the following C program:
#include <stdio.h>
int jumble (int x, int y) {
x = 2 * x + y ;
return x ;
}
int main ( ) {
int x=2, y=5 ;
y = jumble (y, x) ;
x = jumble (y, x) ;
printf ("%d \n", x) ;
return 0 ;
}
The value printed by the program is ______.
26 | |
67 | |
25 | |
13 |
#include
int jumble(int x, int y)
{
printf("Inside jumble : 2*%d + %d\n", x,y);
x = 2*x +y;
return x;
}
int main()
{
int x=2, y=5;
printf("Initial x=%d, y=%d\n",x,y);
printf("1st jumble call : jumble(%d,%d)\n",y,x);
y = jumble(y,x);
printf("Value of y after 1st jumble = %d\n", y);
printf("2nd jumble call: jumble(%d,%d)\n", y,x);
x = jumble(y,x);
printf("Value of x after 2nd jumble = %d\n", x);
printf("Final : %d\n", x);
return 0;
}
////////////////////////////////////OUTPUT
Initial x=2, y=5
1st jumble call: jumble(5,2)
Inside jumble : 2*5 + 2
Value of y after 1st jumble = 12
2nd jumble call: jumble(12,2)
Inside jumble : 2*12 + 2
Value of x after 2nd jumble = 26
Final : 26
Question 13 |
Consider the following C function.
void convert (int n) {
if (n < 0)
printf ("%d", n);
else {
convert (n/2);
printf ("%d", n%2);
}
}
Which one of the following will happen when the function convert is called with any positive integer n as argument?
It will print the binary representation of n in the reverse order and terminate. | |
It will not print anything and will not terminate. | |
It will print the binary representation of n and terminate. | |
It will print the binary representation of n but will not terminate. |
Sequence of function calls
Convert(6)
Convert(3)
Convert(1)
Convert(0)
:
Convert(0)
:
:
It will not terminate and never produce any output.
Note:
There is no instruction which stops the loop.
Question 14 |
How many onto (or surjective) functions are there from an n-element (n ≥ 2) set to a 2-element set?
2n | |
2n-1 | |
2n-2 | |
2(2n– 2) |
Onto function is possible if m ≥ n. So, no. of onto functions possible is,
nm - nC1 (n-1)m + nC2 (n-2)m + .......
Here in Question,
m = n, n = 2
So, the final answer will be,
= 2n - 2C1 (2-1)n + 2C2 (2-2)n
= 2n - 2 × 1 + 0
= 2n - 2
Question 15 |
 Which of the following real values best approximates the value of f(1,3)?
Which of the following real values best approximates the value of f(1,3)?0.2 | |
0.4 | |
0.6 | |
0.8 |
Question 16 |
unsigned int rer ( unsigned int n, unsigned int r){
If (n > 0) return ( n%r + rer (n/r,r));
else return 0;
}
What is the return value of the function rer when it is called as rer (513, 2 )?
9 | |
8 | |
5 | |
2 |
Condition: n>0
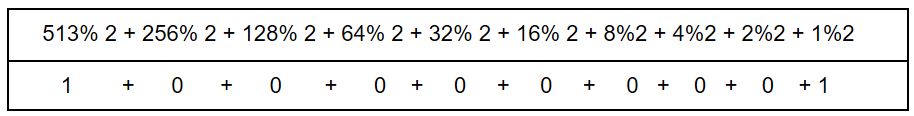
Sum of bits=2 if they given 513. It represented in binary.
Question 17 |
Integer procedure P(X,Y);
Integer X,Y;
value x;
Begin
K=5;
L=8
P=x+y;
End
X is called by value and Y is called by name. If the procedure were invoked by the following program fragment
K=0
L=0
Z=P(K,L);
then the value Z would be set equal to
5 | |
8 | |
13 | |
0 |
Question 18 |
The time complexity of the following C function is (assume n>0)
int recursive (int n)
{
if (n==1) return(1);
else return(recursive (n-1) + recursive(n-1));
}
O(n) | |
O(n log n) | |
O(n2) | |
O(2n) |
Note ‘a’ is a constant O(1) cost that the non-recursive part of the function takes.
Solving the recurrence by Back Substitution:
T(n) = 2T(n-1)+a
T(n-1) = 2T(n-2)+a
T(n-2) = 2T(n-3)+a
:
:
Thus we can write the equation as follows
T(n) = 2(2T(n-2)+a)+a = 4T(n-2) + 2a + a
T(n) = 4(2T(n-3)+a) + 2a + a = 8T(n-3) + 4a + 2a + a
:
:
:
T(n) = 2k T(n-k) + (2k - 1)a
On substituting limiting condition,
T(1) = 1
=> n - k = 1
=> k = n-1
Therefore, our solution becomes
2n-1 + (2n-1 - 1)a
= O(2n)
Question 19 |
int function (int x, int y)
{
if(y<=0) return x;
return function (y, x%y);
}
The above recursive function computes ______
GCD of X and Y
| |
xy | |
yx | |
HCF of x and y | |
Both A and D |

