K-Map
Question 1 |
(a) Implement a circuit having the following output expression using an inverter and NAND gate ![]() .
.
(b) What is the equivalent minimal Boolean expression (in sum of products form)
for the Karnaugh map given below?
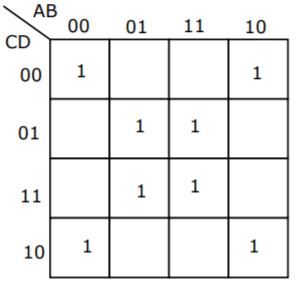
Theory Explanation. |
Question 2 |
What is the equivalent Boolean expression in product-of-sums form for the Karnaugh map given below.
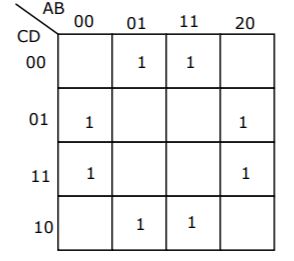
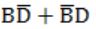 | |
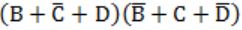 | |
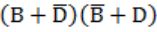 | |
 | |
None of the above |
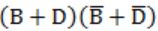

Question 3 |
Let f(x, y, z) = x' + y'x + xz be a switching function. Which one of the following is valid?
 | |
xz is a minterm of f | |
xz is an implicant of f | |
y is a prime implicant of f |
Question 4 |
Consider the minterm list form of a Boolean function F given below.
- F(P, Q, R, S) = Σm(0, 2, 5, 7, 9, 11) + d(3, 8, 10, 12, 14)
Here, m denotes a minterm and d denotes a don’t care term. The number of essential prime implicants of the function F is _______.
3 | |
4 | |
5 |
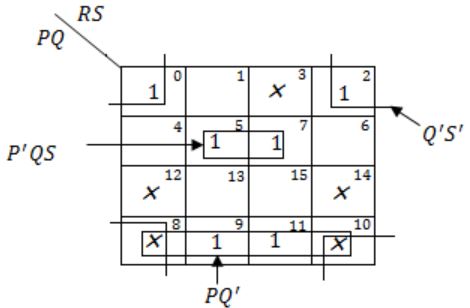
There are 3 prime implicant i.e., P’QS, Q’S’ and PQ’ and all are essential.
Because 0 and 2 are correct by only Q’S’, 5 and 7 are covered by only P’QS and 8 and 9 are covered by only PQ’.
Question 5 |
The function represented by the Karnaugh map given below is:
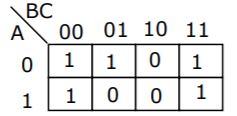
A⋅B | |
AB+BC+CA | |
 | |
None of the above |
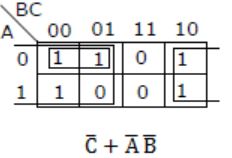
Question 6 |
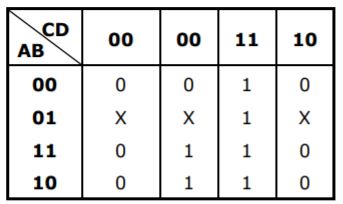
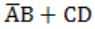 | |
 | |
 | |
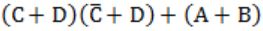 |

⇒ CD+AD = D(A+C)
Question 7 |
Which function does NOT implement the Karnaugh map given below?

(w + x)y | |
xy + yw | |
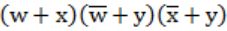 | |
None of the above |
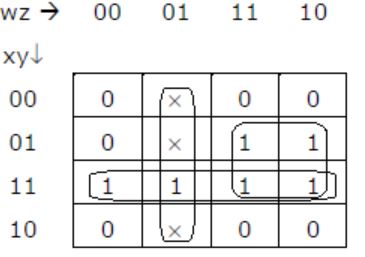
⇒ wy + wz + xy
Question 8 |
Given the following Karnaugh map, which one of the following represents the minimal Sum-Of-Products of the map?

xy+y'z | |
wx'y'+xy+xz | |
w'x+y'z+xy | |
xz+y |
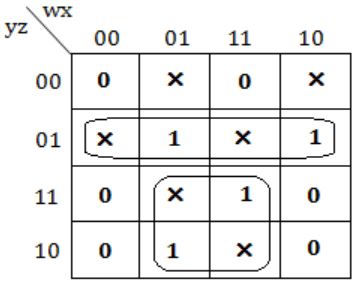
⇒ y'z + xy
Question 9 |
Minimum sum of product expression for f(w,x,y,z) shown in Karnaugh-map below is

xz+y'z | |
xz'+zx' | |
x'y+zx' | |
None of the above |
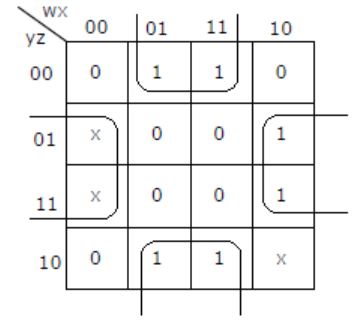
⇒ xz' + zx'
Question 10 |
The literal count of a boolean expression is the sum of the number of times each literal appears in the expression. For example, the literal count of (xy + xz') is 4. What are the minimum possible literal counts of the product-of-sum and sum-of-product representations respectively of the function given by the following Karnaugh map ? Here, X denotes "don't care"

(11, 9) | |
(9, 13) | |
(9, 10) | |
(11, 11) |

⇒ w'y' + z'wx' + xyz'
Total 8 literals are there.
For POS,
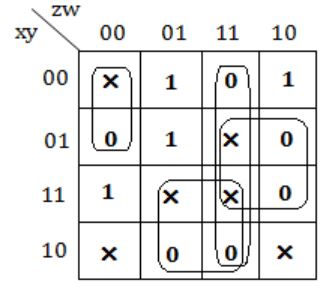
⇒ (z' + w')(z' + y')(w' + x')(x + z + w)
Total 9 literals are there.
