Logic-Gates
Question 1 |
Consider the Boolean function z(a,b,c).

Which one of the following minterm lists represents the circuit given above?
Z = ∑(0,1,3,7) | |
Z = ∑(2,4,5,6,7) | |
Z = ∑(1,4,5,6,7) | |
Z = ∑(2,3,5) |
Convert a+b’c into canonical form which is sum of minterms.
a + b’c = a(b + b’)(c + c’) + (a + a’)b’c
= abc + abc’ + ab’c + ab’c’ + ab’c + a’b’c
= Σ(7,6,5,4,1)
Question 2 |
Let ⊕ and ⊙ denote the Exclusive OR and Exclusive NOR operations, respectively. Which one of the following is NOT CORRECT?
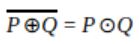 | |
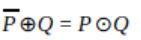 | |
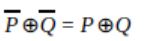 | |
 |

Question 3 |
Which of the following operations is commutative but not associative?
AND | |
OR | |
NAND | |
EXOR |
Question 4 |
(a) The implication gate shown below, has two inputs (x and y), the output is 1 except when x=1 and y=0. Realize f = x'y + xy' using only four implication gates.

(b) Show that the implication gate is functionally complete.
Theory Explanation. |
Question 5 |
 ?
?x NAND X | |
x NOR x | |
x NAND 1 | |
x NOR 1 |

Question 6 |
Consider the circuit shown below. In a certain steady state, the line Y is at '1'. What are the possible values of A, B and C in this state?

A = 0, B = 0, C = 1 | |
A = 0, B = 1, C = 1 | |
A = 1, B = 0, C = 1 | |
A = 1, B = 1, C = 1 |
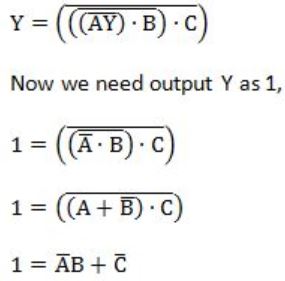
So the above equation is satisfied if either C=0 or A=0 and B=1.
Hence, Option (B) is correct.
Question 7 |
Consider the following circuit composed of XOR gates and non-inverting buffers.
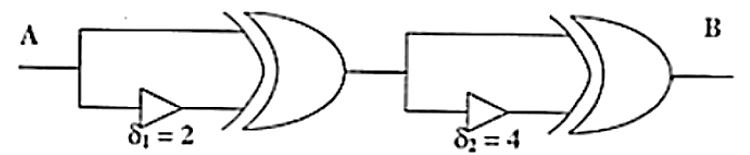
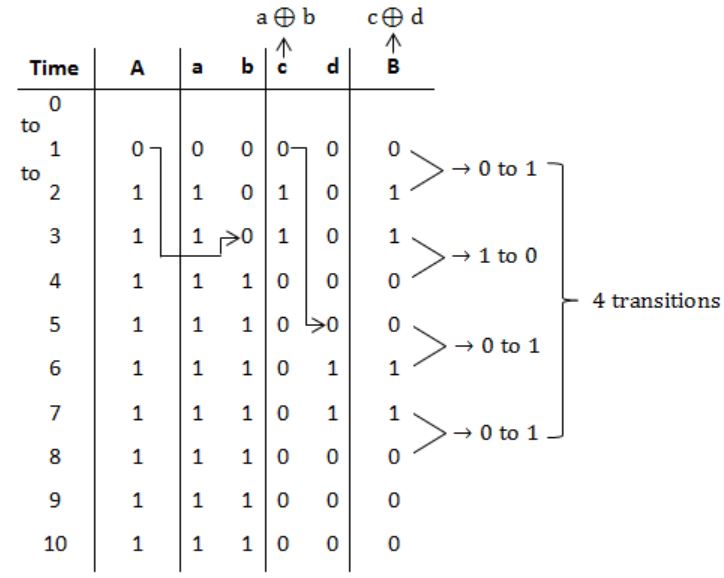
The non-inverting buffers have delays δ1 = 2 ns and δ2 = 4 ns as shown in the figure. Both XOR gates and all wires have zero delay. Assume that all gate inputs, outputs and wires are stable at logic level 0 at time 0. If the following waveform is applied at input A, how many transition(s) (change of logic levels) occur(s) at B during the interval from 0 to 10 ns?

1 | |
2 | |
3 | |
4 |
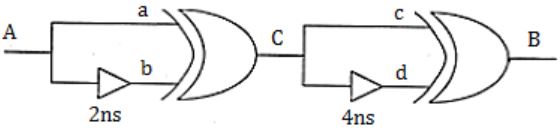
⇒ a will always be equal to A.
Question 8 |
The logic expression for the output of the circuit shown in figure below is:

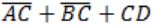 | |
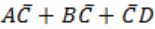 | |
 | |
 | |
None of the above. |
Question 9 |
(a) Assume that a CPU has only two registers R1 and R2 and that only the following instruction is available XOR Ri, Rj; {Rj ← Ri ⊕ Rj, for i,j = 1,2}
Using this XOR instruction, find an instruction sequence in order to exchange
the contents of the registers R1 and R2.
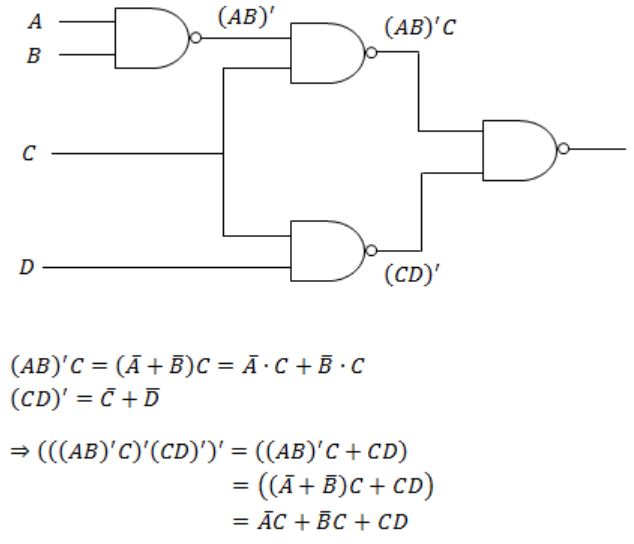
(b) The line p of the circuit shown in figure has stuck at 1 fault. Determine an input test to detect the fault.
Theory Explanation. |
Question 10 |
Identify the logic function performed by the circuit shown in figure.
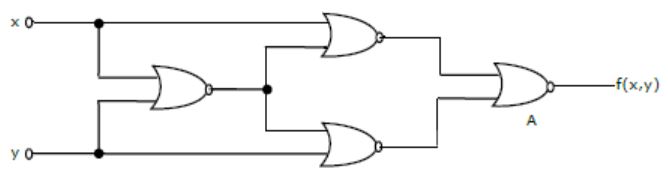
exclusive OR | |
exclusive NOR | |
NAND | |
NOR |

So finally, we can write

Question 11 |
What is the minimum number of NAND gates required to implement a 2-input EXCLUSIVE-OR function without using any other logic gate?
3 | |
4 | |
5 | |
6 |

To create 2-input Exclusive-OR function we require 4 NAND gates.
Question 12 |
What is the minimum number of 2-input NOR gates required to implement a 4-variable function function expressed in sum-of-minterms form as f = Σ(0, 2, 5, 7, 8, 10, 13, 15)? Assume that all the inputs and their complements are available.
2 | |
4 | |
7 | |
1 | |
3(Option not given) |


Question 13 |
Consider three 4-variable functions f1, f2 and f3, which are expressed in sum-of-minterms as
f1 = Σ(0, 2, 5, 8, 14), f2 = Σ(2, 3, 6, 8, 14, 15), f3 = Σ(2, 7, 11, 14)
For the following circuit with one AND gate and one XOR gate, the output function f can be expressed as:
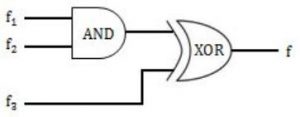
Σ (2, 14) | |
Σ (7, 8, 11) | |
Σ (2, 7, 8, 11, 14) | |
Σ (0, 2, 3, 5, 6, 7, 8, 11, 14, 15) |
f3 = ∑(2,7,11,14)
f1*f2 ⊕ f3 = ∑(2,8,14) ⊕ ∑(2,7,11,14)
= ∑(8,7,11)
(Note: Choose the terms which are not common)
Question 14 |
What is the Boolean expression for the output f of the combinational logic circuit of NOR gates given below?
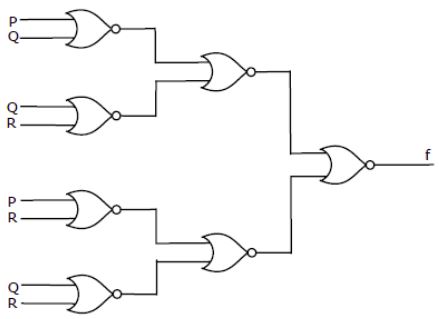
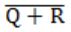 | |
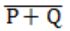 | |
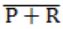 | |
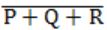 |
= (P’Q’ + Q’R’)( P’R’ + Q’R’)
= (P’Q’P’R’ + P’Q’Q’R’ + Q’R’P’R’ + Q’R’Q’R’)
= (P’Q’R’ + P’Q’R’ + P’Q’R’ + Q’R’)
= (P’Q’R’ + Q’R’)
= (Q’R’)
= (Q+R)’
