Software-Reliability
Question 1 |
The following table shoes the time between failures for a software system
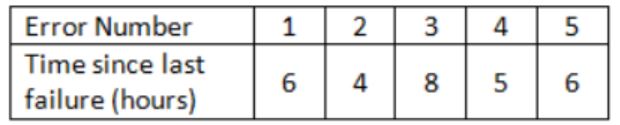
The reliability of the system for one hour of operation assuming an exponential model is
0.45 | |
0.63 | |
0.84 | |
0.95 |
Question 1 Explanation:
MIBF = ∑(Start of downtime - Start of uptime)/No. of failures
MIBF = (6+4+8+5+6)/5 = 29/5
The probability or reliability that the product will work for a defined period of time without failure is given by
R(T) = exp(-T/MTBF); T = 1 hour
R(1) = e(-1/(29/5)) = e(-5/29) = 0.84
MIBF = (6+4+8+5+6)/5 = 29/5
The probability or reliability that the product will work for a defined period of time without failure is given by
R(T) = exp(-T/MTBF); T = 1 hour
R(1) = e(-1/(29/5)) = e(-5/29) = 0.84
Question 2 |
Software reliability is described with respect to
(A) Execution Time
(B) Calendar Time
(C) Clock Time
Choose the correct answer from the options given below:
(A) and (B) only | |
(B) and (C) only | |
(A), (B) and (C)
| |
(A) and (C) only |
Question 2 Explanation:
Software reliability testing is a field of software-testing that relates to testing a software's ability to function(which is related execution), given environmental conditions, for a particular amount of time(related to clock). Software reliability testing helps discover many problems in the software design and functionality.
Software reliability is also related to the ability of software to execute for a long period of time without any failure, which in turn related to calendar time.
Software reliability is also related to the ability of software to execute for a long period of time without any failure, which in turn related to calendar time.
Question 3 |
A server crashes on average once in 30 days, that is, the Mean Time Between Failures (MTBF) is 30 days. When this happens, it takes 12 hours to reboot it, that is, the Mean Time to Repair (MTTR) is 12 hours. The availability of server with these reliability data values is approximately :
96.3% | |
97.3% | |
98.3% | |
99.3% |
Question 3 Explanation:
Given data,
-- Mean Time Between Failures (MTBF)= 30 days
-- Mean Time to Repair (MTTR) =12 hours.
-- Availability=?
Step-1: First we have to convert number of days into hours
30 days= 30 * 24 = 720 hour.
Step-2: The availability of a system is
Availability = MTBF / (MTBF + MTTR)
= 720 / (720 + 12)
= 0.9836 (or) 98.36%
-- Mean Time Between Failures (MTBF)= 30 days
-- Mean Time to Repair (MTTR) =12 hours.
-- Availability=?
Step-1: First we have to convert number of days into hours
30 days= 30 * 24 = 720 hour.
Step-2: The availability of a system is
Availability = MTBF / (MTBF + MTTR)
= 720 / (720 + 12)
= 0.9836 (or) 98.36%
There are 3 questions to complete.
