Sorting
Question 1 |
Merge sort uses
Divide and conquer strategy | |
Backtracking approach | |
Heuristic search | |
Greedy approach |
Question 2 |
Consider the following sequence of numbers
92, 37, 52, 12, 11, 25
Use bubble sort to arrange the sequence in ascending order. Give the sequence at the end of each of the first five passes.
Theory Explanation. |
Question 3 |
A two dimensional array A[1...n][1...n] of integers is partially sorted if
∀i, j ∈ [1...n−1], A[i][j] < A[i][j+1] and
A[i][j] < A[i+1][j]
Fill in the blanks:
(a) The smallest item in the array is at A[i][j] where i=............and j=..............
(b) The smallest item is deleted. Complete the following O(n) procedure to insert item x (which is guaranteed to be smaller than any item in the last row or column) still keeping A partially sorted.
procedure insert (x: integer);
var i,j: integer;
begin
(1) i:=1; j:=1, A[i][j]:=x;
(2) while (x > ...... or x > ......) do
(3) if A[i+1][j] < A[i][j] ......... then begin
(4) A[i][j]:=A[i+1][j]; i:=i+1;
(5) end
(6) else begin
(7) ............
(8) end
(9) A[i][j]:= .............
end
Theory Explanation. |
Question 4 |
A sorting technique is called stable if
it takes O (nlog n) time | |
it maintains the relative order of occurrence of non-distinct elements | |
it uses divide and conquer paradigm | |
it takes O(n) space |
Question 5 |
If one uses straight two-way merge sort algorithm to sort the following elements in ascending order:
20, 47, 15, 8, 9, 4, 40, 30, 12, 17
then the order of these elements after second pass of the algorithm is:
8, 9, 15, 20, 47, 4, 12, 17, 30, 40 | |
8, 15, 20, 47, 4, 9, 30, 40, 12, 17 | |
15, 20, 47, 4, 8, 9, 12, 30, 40, 17 | |
4, 8, 9, 15, 20, 47, 12, 17, 30, 40 |

Question 6 |
Let s be a sorted array of n integers. Let t(n) denote the time taken for the most efficient algorithm to determined if there are two elements with sum less than 1000 in s. Which of the following statements is true?
t(n) is O(1) | |
n ≤ t(n) ≤ n log2 n | |
n log2 n ≤ t(n) < (n/2) | |
t(n) = (n/2) |
Question 7 |
Randomized quicksort is an extension of quicksort where the pivot is chosen randomly. What is the worst case complexity of sorting n numbers using randomized quicksort?
O(n) | |
O(n log n) | |
O(n2) | |
O(n!) |
Question 8 |
In a permutation a1...an of n distinct integers, an inversion is a pair (ai, aj) such that i < j and ai > aj.
If all permutations are equally likely, what is the expected number of inversions in a randomly chosen permutation of 1...n ?
n(n-1)/2 | |
n(n-1)/4 | |
n(n+1)/4 | |
2n[log2n] |
Question 9 |
In a permutation a1...an of n distinct integers, an inversion is a pair (ai, aj) such that i
What would be the worst case time complexity of the Insertion Sort algorithm, if the inputs are restricted to permutations of 1...n with at most n inversions?
Θ(n2) | |
Θ(n log n) | |
Θ(n1.5) | |
Θ(n) |
Question 10 |
Consider the recursive algorithm given below:
procedure bubblersort (n);
var i,j: index; temp : item;
begin
for i:=1 to n-1 do
if A[i] > A [i+1] then
begin
temp : A[i];
A[i]:=A[i+1];
A[i+1]:=temp
end;
bubblesort (n-1)
end
Let an be the number of times the ‘if…then….’ Statement gets executed when the algorithm is run with value n. Set up the recurrence relation by defining an in terms of an-1. Solve for an.
Theory Explanation. |
Question 11 |
Following algorithm(s) can be used to sort n integers in the range [1...n3] in O(n) time
Heapsort | |
Quicksort | |
Mergesort | |
Radixsort |
As Radix sort is not comparison based sort (it is counting sort), so can be done in linear time.
Question 12 |
Let a and b be two sorted arrays containing n integers each, in non-decreasing order. Let c be a sorted array containing 2n integers obtained by merging the two arrays a and b. Assuming the arrays are indexed starting from 0, consider the following four statements
1. a[i] ≥ b [i] => c[2i] ≥ a [i] 2. a[i] ≥ b [i] => c[2i] ≥ b [i] 3. a[i] ≥ b [i] => c[2i] ≤ a [i] 4. a[i] ≥ b [i] => c[2i] ≤ b [i]Which of the following is TRUE?
only I and II | |
only I and IV | |
only II and III | |
only III and IV |
Since both 'a' and 'b' are sorted in the beginning, there are 'i' elements than or equal to a[i] and similarly 'i' elements smaller than or equal to b[i]. So, a[i] ≥ b[i] means there are 2i elements smaller than or equal to a[i] and hence in the merged array, a[i] will come after these 2i elements. So, c[2i] ≤ a[i].
Similarly, a[i] ≥ b[i] says for b that, there are not more than 2i elements smaller than b[i] in the sorted array. So, b[i] ≤ c[2i].
So, option (C) is correct.
Question 13 |
If we use Radix Sort to sort n integers in the range [nk/2, nk], for some k>0 which is independent of n, the time taken would be?
Θ(n) | |
Θ(kn) | |
Θ(nlogn) | |
Θ(n2) |
where n = keys, w = word size
w = log2 (nk) = k × log2 (n)
Complexity Θ(wn) = Θ(k × log2(n) × n) = Θ(n log n) = Θ(n log n)
Question 14 |
Let P be a quicksort program to sort numbers in ascending order. Let t1 and t2 be the time taken by the program for the inputs [1 2 3 4] and [5 4 3 2 1] respectively. Which of the following holds?
t1 = t2 | |
t1 > t2 | |
t1 < t2 | |
t1 = t2 + 5 log 5 |
Question 15 |
Quicksort is ________ efficient than heapsort in the worst case.
LESS. |
Question 16 |
The minimum number of comparisons required to sort 5 elements is _____
7 |
= ⌈log(n!)⌉
= ⌈log(5!)⌉
= ⌈log(120)⌉
= 7
Question 17 |
I. Quicksort runs in Θ(n2) time
II. Bubblesort runs in Θ(n2) time
III. Mergesort runs in Θ(n) time
IV. Insertion sort runs in Θ(n) time
I and II only | |
I and III only | |
II and IV only | |
I and IV only |
→ The recurrence relation for Quicksort, if elements are already sorted,
T(n) = T(n-1)+O(n) with the help of substitution method it will take O(n2).
→ The recurrence relation for Merge sort, is elements are already sorted,
T(n) = 2T(n/2) + O(n) with the help of substitution method it will take O(nlogn).
We can also use master's theorem [a=2, b=2, k=1, p=0] for above recurrence.
Question 18 |
An array of 25 distinct elements is to be sorted using quicksort. Assume that the pivot element is chosen uniformly at random. The probability that the pivot element gets placed in the worst possible location in the first round of partitioning (rounded off to 2 decimal places) is _____.
0.08 | |
0.01 | |
1 | |
8 |
Step-2: Pivot element = uniformly random.
Step-3: Worst case position in the pivot element is either first (or) last.
Step-4: So total 2 possibilities among 25 distinct elements
= 2/25
= 0.08
Question 19 |
There are n unsorted arrays: A1, A2, ..., An. Assume that n is odd. Each of A1, A2, ..., An contains n distinct elements. There are no common elements between any two arrays. The worst-case time complexity of computing the median of the medians of A1, A2, ..., An is
O(n) | |
O(n log n) | |
Ω(n2 log n) | |
O(n2) |
But it is similar to quicksort but in quicksort, partitioning will take extra time.
→ Find the median will be (i+j)/2
1. If n is odd, the value is Ceil((i+j)/2)
2. If n is even, the value is floor((i+j)/2)
-> Here, total number of arrays are
⇒ O(n)*O(n)
⇒ O(n2)
Note:
They are clearly saying that all are distinct elements.
There is no common elements between any two arrays.
Question 20 |
The worst case running times of Insertion sort, Merge sort and Quick sort, respectively, are:
Θ(nlogn), Θ(nlogn), and Θ(n2) | |
Θ(n2 ), Θ(n2 ), and Θ(nlogn) | |
Θ(n2), Θ(nlogn), and Θ(nlogn) | |
Θ(n2), Θ(nlogn), and Θ(n2) |

Question 21 |
What is the number of swaps required to sort n elements using selection sort, in the worst case?
θ(n) | |
θ(n log n) | |
θ(n2) | |
θ(n2 logn) |
Question 22 |
In quick sort, for sorting n elements, the (n/4)th smallest element is selected as pivot using an O(n) time algorithm. What is the worst case time complexity of the quick sort?
θ(n) | |
θ(n log n) | |
θ(n2) | |
θ(n2 log n) |
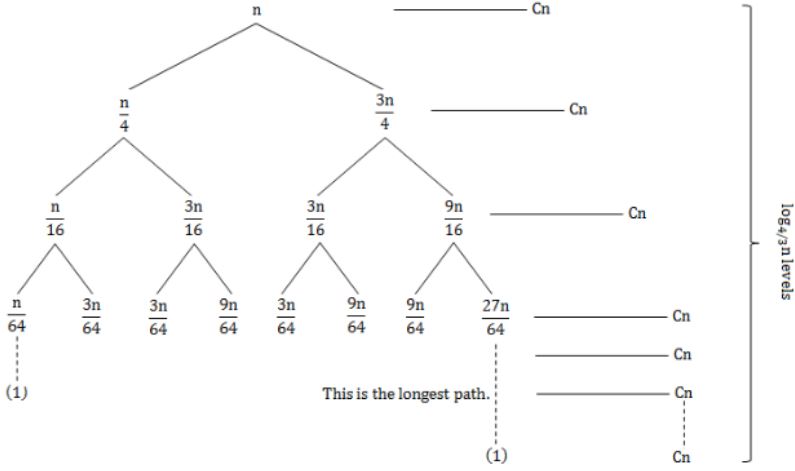
n→n/(4/3)→n/(4/3)2→n/(4/3)3-----n/(4/3)k=1
n/(4/3)k = 1
⇒n=(4/3)k ⇒ k = log4/3n [k=no. of levels]
In each level workdone = Cn
So, total workdone = Cn⋅log4/3n = (nlog4/3n)
Question 23 |
Consider the Quicksort algorithm. Suppose there is a procedure for finding a pivot element which splits the list into two sub-lists each of which contains at least one-fifth of the elements. Let T(n) be the number of comparisons required to sort n elements. Then
T(n) ≤ 2T(n/5) + n
| |
T(n) ≤ T(n/5) + T(4n/5) + n | |
T(n) ≤ 2T(4n/5) + n | |
T(n) ≤ 2T(n/2) + n
|
So, T(n/5) comparisons are needed for the first subset and T(4n/5) comparisons needed for second subset.
Now, suppose that one subset contains more than n/5 elements then another subset will contain less than 4n/5 elements. Due to which time complexity will be less than
T(n/5) + T(4n/5) + n
Because recursion tree will be more balanced.
Question 24 |
Which one of the following is the tightest upper bound that represents the number of swaps required to sort n numbers using selection sort?
O(log n) | |
O(n) | |
O(n log n) | |
O(n2) |
Selection sort time complexity O(n2) in terms of number of comparisons. Each of these scans requires one swap for n-1 elements (the final element is already in place).
Question 25 |
The number of elements that can be sorted in Θ(log n) time using heap sort is
Θ(1) | |
Θ(√logn) | |
Θ (logn/loglogn) | |
Θ(log n) |
So, Θ((logn/ log log n)log(logn/log log n))
= Θ(logn/log logn (log logn - log log logn))
= Θ((log n/log logn) × log log n)
= Θ(log n)
Hence, option (C) is correct answer.
Question 26 |
You have an array of n elements. Suppose you implement quicksort by always choosing the central element of the array as the pivot. Then the tightest upper bound for the worst case performance is
O(n2) | |
O(n log n) | |
Θ(n logn) | |
O(n3) |
Question 27 |
Which one of the following in place sorting algorithms needs the minimum number of swaps?
Quick sort | |
Insertion sort | |
Selection sort | |
Heap sort |
Question 28 |
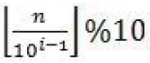 | |
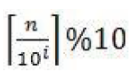 | |
 | |
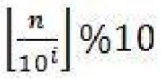 |
Question 29 |
001<010<011<0001<0101 | |
0001<001<010<0101<011 | |
0001<0101<001<010<011 | |
001<010<0001<0101<011 |
0001<001<010<0101<011
Note: Lexicographical order is nothing but dictionary based order.
Question 30 |
Impossible to sort in linear time | |
Radix Sort | |
Insertion Sort | |
Bubble Sort |
Even it gives linear time when the input array is 0 to n^6….
Question 31 |
4 | |
2 | |
1 | |
3 |

Note: Official answer key given, Option-D as the correct answer.
Question 32 |
function mystery (A[0..99]) {
int i,j,m;
for (i = 0; i < 100; i++) {
m = i;
for (j = i; j < 100, j++) {
if (A[j] > A[m]) {
m = j;
}
}
reverse(A,i,m);
}
return;
}
When the procedure terminates, the array A has been:
Sorted in descending order | |
Sorted in ascending order | |
Reversed | |
Left unaltered |
Question 33 |
Insertion sort | |
Quick sort | |
Merge sort | |
Selection sort |

Question 34 |
67, 12, 10, 5, 4, 7, 23 | |
4, 7, 10, 23, 67, 12, 5 | |
4, 5, 7, 67, 10, 12, 23 | |
10, 7, 4, 67, 23, 12, 5 |
Pass-1: 4, 10, 7, 23, 67, 12, 5
Pass-2: 4, 7, 10, 23, 67, 12, 5
Pass-3: 4, 7, 10, 23, 67, 12, 5 [ No change because the value 10 is placed in the same position ]
Question 35 |
O(n) | |
O(1) | |
O(n2) | |
O(n log n) |
Question 36 |
Merge sort | |
Radix sort | |
Heap sort | |
Address Calculation Sort |
Merge sort has space complexity of O(n). Hence it is not an in-place sorting algorithm.
