UGC NET Dec-2020 and June-2021 Paper-2
October 6, 2023NIC-NIELIT Scientist-B 2020
October 6, 2023Theory-of-Computation
|
Question 14
|
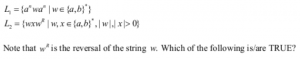
|
L 1 and L 2 are regular.
|
|
|
L 1 and L 2 are context-free.
|
|
|
L 1 is regular and L 2 is context-free.
|
|
|
L 1 and L 2 are context-free but not regular.
|
Question 14 Explanation:
Both L1 and L2 are regular.
Since no condition on the value of “n” is mentioned so for a particular case we can assume n=0, now when n=0 the language L1= w =(a+b)*
So if one case is (a+b)* then now even we assume any value of “n” the generated string will already present in (a+b)* thus L1=(a+b)*.
L2: In L2 the middle X can expand and consume all symbols of w except the first symbol and symbols of wr except the last symbol so L2 will be equivalent to language all strings start and end with the same symbol, hence L2 is regular.
Since no condition on the value of “n” is mentioned so for a particular case we can assume n=0, now when n=0 the language L1= w =(a+b)*
So if one case is (a+b)* then now even we assume any value of “n” the generated string will already present in (a+b)* thus L1=(a+b)*.
L2: In L2 the middle X can expand and consume all symbols of w except the first symbol and symbols of wr except the last symbol so L2 will be equivalent to language all strings start and end with the same symbol, hence L2 is regular.
Correct Answer: C
Question 14 Explanation:
Both L1 and L2 are regular.
Since no condition on the value of “n” is mentioned so for a particular case we can assume n=0, now when n=0 the language L1= w =(a+b)*
So if one case is (a+b)* then now even we assume any value of “n” the generated string will already present in (a+b)* thus L1=(a+b)*.
L2: In L2 the middle X can expand and consume all symbols of w except the first symbol and symbols of wr except the last symbol so L2 will be equivalent to language all strings start and end with the same symbol, hence L2 is regular.
Since no condition on the value of “n” is mentioned so for a particular case we can assume n=0, now when n=0 the language L1= w =(a+b)*
So if one case is (a+b)* then now even we assume any value of “n” the generated string will already present in (a+b)* thus L1=(a+b)*.
L2: In L2 the middle X can expand and consume all symbols of w except the first symbol and symbols of wr except the last symbol so L2 will be equivalent to language all strings start and end with the same symbol, hence L2 is regular.
Subscribe
Login
0 Comments
