Aptitude
October 10, 2023Programming
October 10, 2023UGC NET CS 2014 June-paper-2
|
Question 10
|
The regular grammar for the language
L = {w|na(w) and nb(w) are both even,
w ∈ {a, b}*} is given by :
(Assume, p, q, r and s are states)
L = {w|na(w) and nb(w) are both even,
w ∈ {a, b}*} is given by :
(Assume, p, q, r and s are states)
|
p → aq | br | λ, q → bs | ap
r → as | bp, s → ar | bq, p and s are initial and final states. |
|
|
p → aq | br, q → bs | ap
r → as | bp, s → ar | bq, p and s are initial and final states. |
|
|
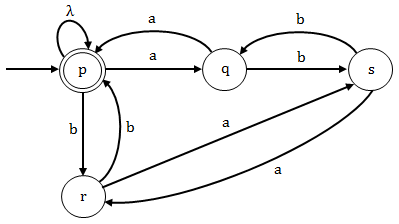
p → aq | br | λ, q → bs | ap
r → as | bp, s → ar | bq p is both initial and final states. |
|
|
p → aq | br, q → bs | ap
r → as | bp, s → ar | bq p is both initial and final states |
Question 10 Explanation:
L={ λ. ab, λab, λaabb, aabb, ……….}
Option (A): The grammar given in this option does not contain a state which is accepting a terminal “λ” , having zero number of “a” and “b”. Since the grammar is not accepting λ so it not the regular grammar for the given language L.
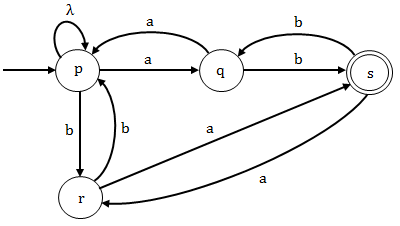
Option (B): The grammar given in this option is not generating any string “λ” which is having zero number of “a” and “b”. Since the grammar is not generating λ so it not the regular grammar for the given language L.

Option (C): Here state “p” is the initial and final state and the grammar given here is generating string “λ” , having zero number of “a” and “b”. Since the grammar is accepting λ so it is the regular grammar for the given language L.
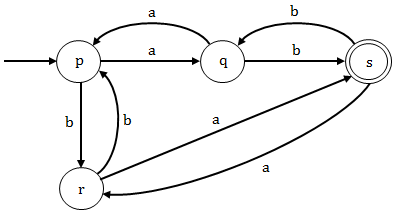
Option (D): In this option (p) is the initial and final state but the grammar is not generating any string “λ” which also belongs to the given language L. So this grammar is not the regular grammar for the given language L.
Option (A): The grammar given in this option does not contain a state which is accepting a terminal “λ” , having zero number of “a” and “b”. Since the grammar is not accepting λ so it not the regular grammar for the given language L.

Option (B): The grammar given in this option is not generating any string “λ” which is having zero number of “a” and “b”. Since the grammar is not generating λ so it not the regular grammar for the given language L.

Option (C): Here state “p” is the initial and final state and the grammar given here is generating string “λ” , having zero number of “a” and “b”. Since the grammar is accepting λ so it is the regular grammar for the given language L.

Option (D): In this option (p) is the initial and final state but the grammar is not generating any string “λ” which also belongs to the given language L. So this grammar is not the regular grammar for the given language L.

Correct Answer: C
Question 10 Explanation:
L={ λ. ab, λab, λaabb, aabb, ……….}
Option (A): The grammar given in this option does not contain a state which is accepting a terminal “λ” , having zero number of “a” and “b”. Since the grammar is not accepting λ so it not the regular grammar for the given language L.

Option (B): The grammar given in this option is not generating any string “λ” which is having zero number of “a” and “b”. Since the grammar is not generating λ so it not the regular grammar for the given language L.

Option (C): Here state “p” is the initial and final state and the grammar given here is generating string “λ” , having zero number of “a” and “b”. Since the grammar is accepting λ so it is the regular grammar for the given language L.

Option (D): In this option (p) is the initial and final state but the grammar is not generating any string “λ” which also belongs to the given language L. So this grammar is not the regular grammar for the given language L.

Option (A): The grammar given in this option does not contain a state which is accepting a terminal “λ” , having zero number of “a” and “b”. Since the grammar is not accepting λ so it not the regular grammar for the given language L.

Option (B): The grammar given in this option is not generating any string “λ” which is having zero number of “a” and “b”. Since the grammar is not generating λ so it not the regular grammar for the given language L.

Option (C): Here state “p” is the initial and final state and the grammar given here is generating string “λ” , having zero number of “a” and “b”. Since the grammar is accepting λ so it is the regular grammar for the given language L.

Option (D): In this option (p) is the initial and final state but the grammar is not generating any string “λ” which also belongs to the given language L. So this grammar is not the regular grammar for the given language L.

Subscribe
Login
0 Comments
