Question 3760 – UGC NET CS 2015 Jun- paper-2
May 9, 2024Question 3814 – UGC NET CS 2015 Jun- paper-2
May 9, 2024Question 3762 – UGC NET CS 2015 Jun- paper-2
Match the following:
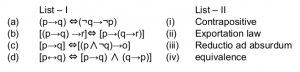
Correct Answer: A
Question 9 Explanation:
→ In logic, contraposition is an inference that says that a conditional statement is logically equivalent to its contrapositive. The contrapositive of the statement has its antecedent and consequent inverted and flipped: the contrapositive of P → Q is thus as ~Q → ~P.
→ The equivalence relation translates verbally into “if and only if” and is symbolized by a double-lined, double arrow pointing to the left and right (↔). If A and B represent statements, then A ↔ B means “A if and only if B.”
→ The exportation rule is a rule in logic which states that “if (P and Q), then R” is equivalent to “if P then (if Q then R)”.
→ The exportation rule may be formally stated as: (P ∧ Q) → R is equivalent to P → (Q →R)
→ A mode of argumentation or a form of argument in which a proposition is disproven by following its implications logically to an absurd conclusion. Arguments that use universals such as, “always”, “never”, “everyone”, “nobody”, etc., are prone to being reduced to absurd conclusions. The fallacy is in the argument that could be reduced to absurdity — so in essence, reductio ad absurdum is a technique to expose the fallacy.
→ The equivalence relation translates verbally into “if and only if” and is symbolized by a double-lined, double arrow pointing to the left and right (↔). If A and B represent statements, then A ↔ B means “A if and only if B.”
→ The exportation rule is a rule in logic which states that “if (P and Q), then R” is equivalent to “if P then (if Q then R)”.
→ The exportation rule may be formally stated as: (P ∧ Q) → R is equivalent to P → (Q →R)
→ A mode of argumentation or a form of argument in which a proposition is disproven by following its implications logically to an absurd conclusion. Arguments that use universals such as, “always”, “never”, “everyone”, “nobody”, etc., are prone to being reduced to absurd conclusions. The fallacy is in the argument that could be reduced to absurdity — so in essence, reductio ad absurdum is a technique to expose the fallacy.
(a)-(i), (b)-(ii), (c)-(iii), (d)-(iv)
(a)-(ii), (b)-(iii), (c)-(i), (d)-(iv)
(a)-(iii), (b)-(ii), (c)-(iv), (d)-(i)
(a)-(iv), (b)-(ii), (c)-(iii), (d)-(i)
Subscribe
Login
0 Comments
