GATE 1993
Question 1 |
The eigen vector(s) of the matrix
is (are)
(0,0,α ) | |
(α,0,0) | |
(0,0,1) | |
(0,α,0) | |
Both B and D |
So the question as has
(A - λI)X = 0
AX = 0
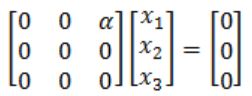
What x1, x2, x3 are suitable?
Which means:
x1 times column 1 + x2 times column 2 + x3 times column 3 = zero vector
Since α is not equal to zero, so x3 must be necessarily zero to get zero vector.
Hence, only (B) and (D) satisfies.
Question 2 |
The differential equation
d2y/dx2 + dy/dx + siny = 0 is:
linear | |
non-linear | |
homogeneous | |
of degree two |
d2y/dx2 + dy/dx + siny = 0
In this DE, degree is 1 then this represent linear equation.
Question 3 |
Simpson’s rule for integration gives exact result when f(x) is a polynomial of degree
1 | |
2 | |
3 | |
4 |
Question 4 |
Which of the following is (are) valid FORTRAN 77 statement(s)?
DO 13 I = 1 | |
A = DIM ***7 | |
READ = 15.0 | |
GO TO 3 = 10 |
Question 5 |
Fourier series of the periodic function (period 2π) defined by

But putting x = π, we get the sum of the series.
π2/4 | |
π2/6 | |
π2/8 | |
π2/12 |
Question 6 |
Which of the following improper integrals is (are) convergent?
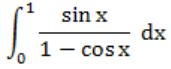 | |
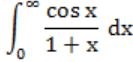 | |
 | |
 |
Question 7 |
The function f(x,y) = x2y - 3xy + 2y + x has
no local extremum | |
one local minimum but no local maximum | |
one local maximum but no local minimum | |
one local minimum and one local maximum |
Question 8 |
1 |
Question 9 |
The radius of convergence of the power series
Out of syllabus. |
Question 10 |
If the linear velocity is given by
The angular velocity at the point (1, 1, -1) is ________
Out of syllabus. |
Question 11 |
Given the differential equation, y′ = x − y with the initial condition y(0) = 0. The value of y(0.1) calculated numerically upto the third place of decimal by the second order Runga-Kutta method with step size h = 0.1 is ________
Out of syllabus. |
Question 12 |
For X = 4.0, the value of I in the FORTRAN 77 statement
1 = -2**2 + 5.0*X/X*3 + 3/4 is _______
Out of syllabus. |
Question 13 |
The value of the double integral is
1/3 |
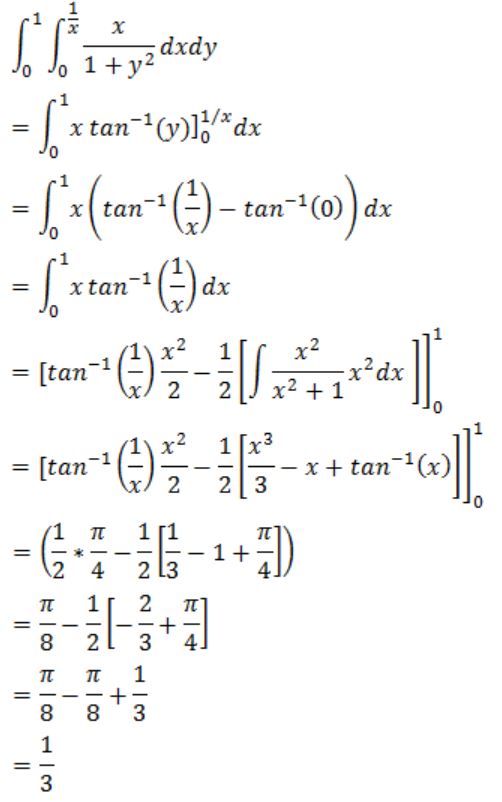
Question 14 |
If 
A4 = I |
(1-λ) (-1-λ) (i-λ) (-i-λ)
= (λ2-1) (λ2+1)
= λ4-1
Characteristic equation is λ4-1 = 0.
According to Cayley-Hamilton theorem, every matrix satisfies its own characteristic equation, so
A4 = I
Question 15 |
Given and S the surface of a unit cube with one corner at the origin and edges parallel to the coordinate axes, the value of integral
Out of syllabus. |
