CHENNAI MATHEMATICAL INSTITUTE M.Sc. / Ph.D. Programme in Computer Science (18 May 2017)
Question 1 |
The regular expression (a ∗ + b) ∗ is equivalent to which of the following regular expressions:
a ∗ b ∗ | |
(a ∗ b + b) ∗ | |
(a + b ∗ ) ∗ | |
(a ∗ b) ∗ |
Question 1 Explanation:
(a ∗ + b) ∗ allows any string over {a, b} and is the same as (a + b) ∗ . Option (a) only allows strings of the form a i b j . Options (b) and (d) do not allow strings of the form a i with no b’s.
Question 2 |
An FM radio channel has a repository of 10 songs. Each day, the channel plays 3 distinct songs that are chosen randomly from the repository.
Mary decides to tune in to the radio channel on the weekend after her exams. What is the probability that no song gets repeated during these 2 days?
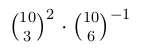 | |
 | |
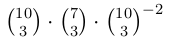 | |
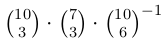 |
Question 2 Explanation:

Question 3 |
Four siblings go shopping with their father. If Abhay gets shoes, then Asha does not get a necklace. If Arun gets a T-shirt, then Aditi gets bangles. If Abhay does not get shoes or Aditi gets bangles, the mother will be happy. Which of the following is true?
If the mother is happy, then Aditi got bangles. | |
If Aditi got bangles, then Abhay got shoes. | |
If the mother is not happy, then Asha did not get a necklace and Arun did not get a T-shirt. | |
None of the above. |
Question 3 Explanation:
Let p denote that Asha get a necklace, q denote that Abhay gets shoes, r denote that Arun gets a T-shirt, s denote that Aditi gets bangles and w denote that mother is happy. The question is equivalent to the formula φ : q → ¬p ∧ r → s ∧ (¬q ∨ s) → w. A formula ψ is a valid implication iff every truth assignment to p, q, r, s, w that makes φ true also makes ψ true. Option (a) is the formula ψ a : w → s, option (b) is the formula ψ b : s → q and option (c) is the formula ψ c : ¬w → (¬p ∧ ¬r). Neither ψ a nor ψ b are valid implications but ψ c is.
Question 4 |
City authorities are concerned about traffic accidents on major roads. They would like to have ambulances stationed at road intersections to quickly reach the scene of any accident along these roads. To minimize response time, ambulances are to be located at intersections with traffic lights so that any segment of road can be reached by at least one ambulance that does not have to pass through a traffic light to reach the scene of the accident. If we model the road network as a graph, where intersections with traffic lights are vertices and edges represent road segments between traffic lights, the graph theoretic question to be answered is:
Find a spanning tree with minimum number of edges. | |
Find a spanning tree with minimum cost. | |
Find a minimal colouring. | |
Find a minimum size vertex cover. |
Question 4 Explanation:
Each ambulance “covers” the adjacent roads, and all roads are covered in this way.
There are 4 questions to complete.
