Database-Management-System
Question 1 |

What does the above expression generate?
A | Employee numbers of all employees whose age is not the maximum. |
B | Employee numbers of only those employees whose age is the maximum. |
C | Employee numbers of all employees whose age is not the minimum. |
D | Employee numbers of only those employees whose age is more than the age of exactly one other employee. |
Question 2 |
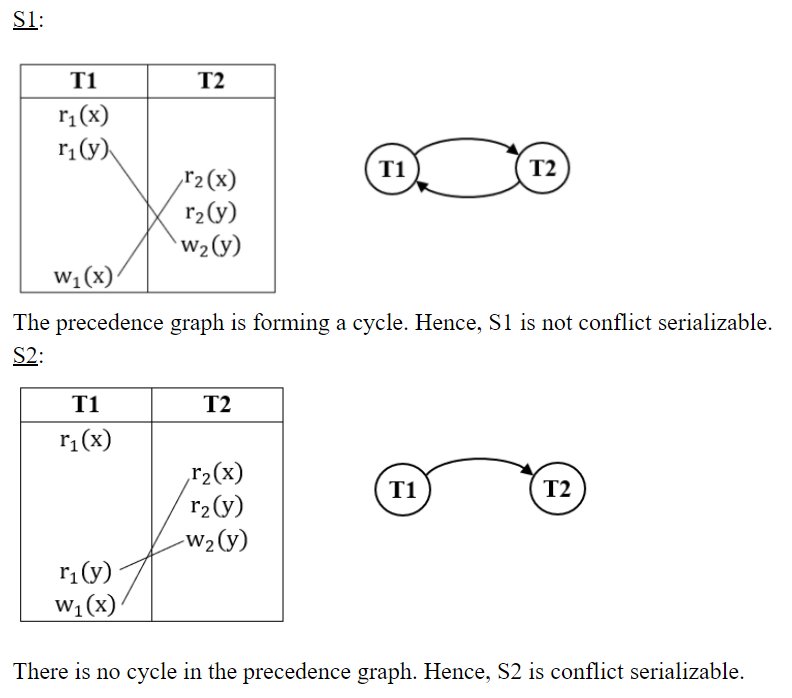
S1: r1(x) r1(y) r2(x) r2(y) w2(y) w1(x)
S2: r1(x) r2(x) r2(y) w2(y) r1(y) w1(x)
Which one of the following options is correct?
A | S1is not conflict serializable, and S2 is conflict serializable. |
B | Neither S1nor S2is conflict serializable.
|
C | Both S1and S2are conflict serializable. |
D | S1is conflict serializable, and S2is not conflict serializable. |
Question 3 |
Consider the decomposition of the relation R into the consistent relations according to the following two decomposition schemes.
D1: R=[(P,Q,S,T); (P,T,X); (Q,Y); (Y,Z,W)]
D2: R=[(P,Q,S);(T,X);(Q,Y);(Y,Z,W)]
Which one of the following options is correct?
A | D1is a lossy decomposition, but D2is a lossless decomposition.
|
B | Both D1and D2are lossy decompositions. |
C | Both D1and D2are lossless decompositions. |
D | D1is a lossless decomposition, but D2is a lossy decomposition. |
Given functional dependencies set:
PQ->X
P->YX
Q->Y
Y->ZW
- While merging the tables there should be some common attribute(s) and it should be a candidate key of one of the tables.
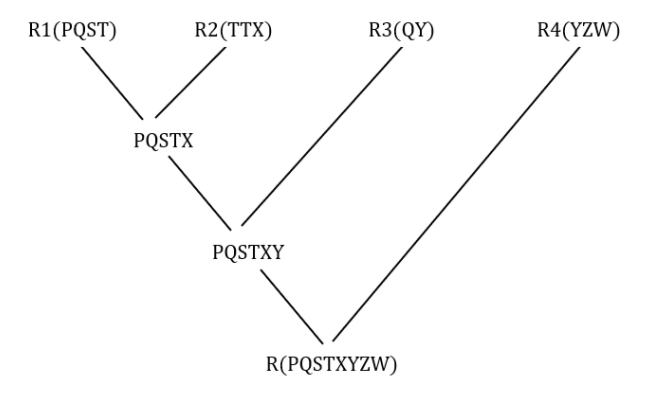
- R1 should be merged with R2 because PT is a key of R2.
- R3 should be merged with PQSTX because Q is a key of R3.
- R4 should be merged with PQSTXY because Y is a key of R4.

- R1 should be merged with R3 because Q is a key of R3.
- R4 should be merged with PQSY because Y is a key of R4.
- Now, there is no common attribute in between R2(TX) and PQSYZW.
- Hence, D2 is lossy decomposition.
Question 4 |
A | The same undo and redo list will be used while recovering again. |
B | The database will become inconsistent. |
C | The system cannot recover any further. |
D | All the transactions that are already undone and redone will not be recovered again. |
Question 5 |

A | 820 |
Explanation :
Probability of 1st condition being satisfied(say P(A)) = 10/15 = 2/3
Probability of 2nd condition being satisfied(say P(B)) = 1/20
Probability of both conditions being satisfied(say P(A intersection B)) = 2/3*1/20 = 1/30
Probability of any one condition being satisfied = P(A union B) = P(A)+P(B)-P(A intersection B) = 2/3 + 1/20 - 1/30 = 41/60
therefore, expected number of tuples = (41/60)*1200 = 820
Question 6 |
The following relations are used to store data about students, courses, enrollment of students in courses and teachers of courses. Attributes for primary key in each relation are marked by ‘*’.
Students (rollno*, sname, saddr) courses (cno*, cname) enroll(rollno*, cno*,grade) teach(tno*,tname,cao*)
(cno is course number, cname is course name, tno is teacher number, tname is teacher name, sname is student name, etc.)
Write a SQL query for retrieving roll number and name of students who got A grade in at least one course taught by teacher named Ramesh for the above relational database.
A | Theory Explanation. |
Question 7 |
The following relations are used to store data about students, courses, enrollment of students in courses and teachers of courses. Attributes for primary key in each relation are marked by ‘*’.
Students (rollno*, sname, saddr) courses (cno*, cname) enroll(rollno*, cno*,grade) teach(tno*,tname,cao*)
(cno is course number, cname is course name, tno is teacher number, tname is teacher name, sname is student name, etc.)
For the relational database given above, the following functional dependencies hold:
rollno → sname,sdaddr cno → cname tno → tname rollno, cno → grade
(a) Is the database in 3rd normal form (3NF)?
(b) If yes, prove that it is in 3 NF. If not, normalize, the relations so that they
are in 3 NF (without proving).
A | Theory Explanation. |
Question 8 |
State True or False with reason
There is always a decomposition into Boyce-Codd normal form (BCNF) that is
lossless and dependency preserving.
A | True |
B | False |
Question 9 |
An instance of a relational scheme R(A, B, C) has distinct values for attribute A.
Can you conclude that A is a candidate key for R?
A | Yes |
B | No |
Question 10 |
Give a relational algebra expression using only the minimum number of operators from (∪, −) which is equivalent to R ∩ S.
A | Out of syllabus (For explanation see below) |
→ No need of using Union operation here. → In question they gave (∪, −) but we don't use both.
→ And also they are saying that only the minimum number of operators from (∪, −) which is equivalent to R ∩ S.
So, the expression is minimal.
Question 11 |
State True or False with reason
Logical data independence is easier to achieve than physical data independence
A | True |
B | False |
Question 12 |
Consider the following relational schema:
COURSES (cno, cname) STUDENTS (rollno, sname, age, year) REGISTERED FOR (cno, rollno)
(a) Write a relational algebra query to
Print the roll number of students who have registered for cno 322.
(b) Write a SQL query to
Print the age and year of the youngest student in each year.
A | Theory Explanation. |
Question 13 |
Consider B+ − tree of order d shown in figure? (A) B+ − tree of order d contains between d and 2d keys in each node. (a) Draw the resulting B+ − tree after inserted in the figure.

(b) For a B+ − tree of order d with n leaf nodes, the number of nodes accessed during a search is 0(-).
A | Theory Explanation. |
Question 14 |
(a) Consider the relation scheme R(A, B, C) with the following functional dependencies:
A, B → C, C → A
Show that the scheme R is the Third Normal Form (3NF) but not in Boyce-Code Normal Form (BCNF).
(b) Determine the minimal keys of relation R.
A | Theory Explanation. |
Question 15 |
Consider the relation scheme.
AUTHOR (ANAME, INSTITUTION, ACITY, AGE) PUBLISHER (PNAME, PCITY) BOOK (TITLE, ANAME, PNAME)
Express the following queries using (one or more of )SELECT, PROJECT, JOIN and DIVIDE operations.
(a) Get the names of all publishers.
(b) Get values of all attributes of all authors who have published a book for the
publisher with PNAME = ‘TECHNICAL PUBLISHERS’.
(c) Get the names of all authors who have published a book for any publisher located in Madras.
A | Theory Explanation. |
Question 16 |
Consider a relational database containing the following schemas.
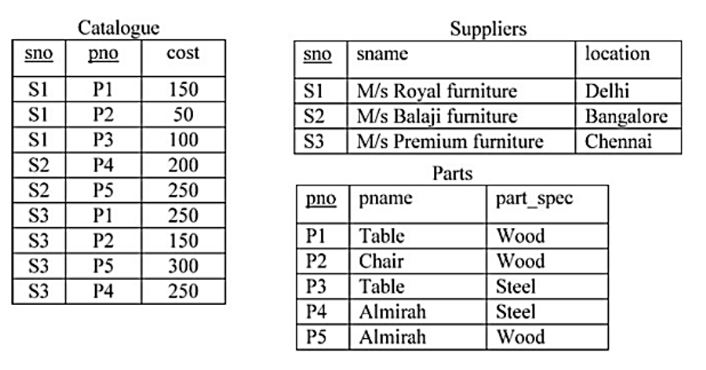
The primary key of each table is indicated by underlying the constituent fields.
SELECT s.sno, s.sname
FROM Suppliers s, Catalogue c
WHERE s.sno = c.sno AND
Cost > (SELECT AVG (cost)
FROM Catalogue
WHERE pno = ‘P4’
GROUP BY pno);
The number of rows returned by the above SQL query is
A | 0 |
B | 5 |
C | 4 |
D | 2 |
AVG(COST)
------------
225
The outer query “select s.sno, s.sname from suppliers s, catalogue c where s.sno=c.sno” returns:
SNO SNAME
----------------------------------------
S1 M/s Royal furniture
S1 M/s Royal furniture
S1 M/s Royal furniture
S2 M/s Balaji furniture
S2 M/s Balaji furniture
S3 M/s Premium furniture
S3 M/s Premium furniture
S3 M/s Premium furniture
S3 M/s Premium furniture
So, the final result of the query is:
SN SNAME
----------------------------------------
S2 M/s Balaji furniture
S3 M/s Premium furniture
S3 M/s Premium furniture
S3 M/s Premium furniture
Therefore, 4 rows will be returned by the query.
Question 17 |
Which one of the following is used to represent the supporting many-one relationships of a weak entity set in an entity-relationship diagram?
A | Ovals that contain underlined identifiers
|
B | Rectangles with double/bold border |
C | Diamonds with double/bold border
|
D | Ovals with double/bold border
|

Question 18 |
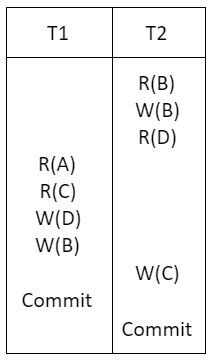
Consider a schedule of transactions T1 and T2:

Here, RX stands for “Read(X)” and WX stands for “Write(X)”. Which one of the following schedules is conflict equivalent to the above schedule?
A |  |
B |  |
C |  |
D |  |
• First, let’s list the conflict operations of each of the schedule given in the options and compare with the conflict operations of schedule which is given in the question.
Given schedule:

Conflict operations:
R2(B) → W1(B)
W2(B) → W1(B)
R1(C) → W2(C)
R2(D) → W1(D)
Option(1):

Conflict operations:
R1(C) → W2(C)
W1(D) → R2(D)
W1(B) → R2(B)
W1(B) → W2(B)
Option(2):
Conflict operations:
R2(B) → W1(B)
W2(B) → W1(B)
R2(D) → W1(D)
R1(C) → W2(C)
Option(3):
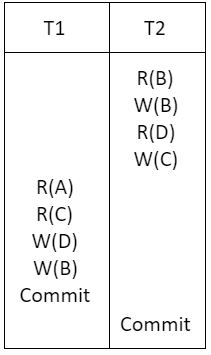
Conflict operations:
R2(B) → W1(B)
W2(B) → W1(B)
R2(D) → W1(D)
W2(C) → R1(C)
Option(4):

Conflict operations:
R1(C) → W2(C)
W1(D) → R2(D)
R2(B) → W1(B)
W2(B) → W1(B)
The conflict operations in the option (2) and given schedule are appearing in the same sequence order, so option (2) is the answer.
Question 19 |
Consider a relational table R that is in 3NF, but not in BCNF. Which one of the following statements is TRUE?
A | A cell in R holds a set instead of an atomic value. |
B | R has a nontrivial functional dependency X→A, where X is not a superkey and A is a non-prime attribute and X is not a proper subset of any key.
|
C | R has a nontrivial functional dependency X→A, where X is not a superkey and A is a non-prime attribute and X is a proper subset of some key. |
D | R has a nontrivial functional dependency X→A, where X is not a superkey and A is a prime attribute. |
FDs:
AB → C
BC → A
(BD)+ = BD ✖
(ABD)+ = ABDC ✔
(CBD)+ = CBDA ✔
Candidate keys = {ABD, CBD}
• The relation R is in 3NF, as there are no transitive dependencies.
• The relation R is not in BCNF, because the left side of both the FD’s are not Super keys.
• In R, BC → A is a non-trivial FD and in which BC is not a Super key and A is a prime attribute.
Question 20 |
Consider a database implemented using B+ tree for file indexing and installed on a disk drive with block size of 4 KB. The size of search key is 12 bytes and the size of tree/disk pointer is 8 bytes. Assume that the database has one million records. Also assume that no node of the B+ tree and no records are present initially in main memory. Consider that each record fits into one disk block. The minimum number of disk accesses required to retrieve any record in the database is ______.
A | 4 |
(1) Database BF = 1
No. of block = 106 } ➝ 1 block access from database
(2) ⎡106/204⎤ = 491
(3) ⎡491/204⎤ = 3
(4) ⎡3/204⎤ = 1
So, 1+3 = 4 disk accesses are required to retrieve any record in the database.
Question 21 |
A library relational database system uses the following schema
USERS (User#, UserName, HomeTown) BOOKS (Book#, BookTitle, AuthorName) ISSUED (Book#, User#, Date)
Explain in one English sentence, what each of the following relational algebra queries is designed to determine
(a) σ User #=6 (11 User #, Book Title ((USERS ISSUED) BOOKS)) (b) σ Author Name (BOOKS (σ Home Town) = Delhi (USERS ISSUED)))
A | Theory Explanation. |
Question 22 |
Which one of the following statements is NOT correct about the B+ tree data structure used for creating an index of a relational database table?
A | Each leaf node has a pointer to the next leaf node |
B | Non-leaf nodes have pointers to data records |
C | B+ Tree is a height-balanced tree |
D | Key values in each node are kept in sorted order |
In B+ trees non-leaf nodes do not have pointers to data records.
Question 23 |
I. Strict two-phase locking protocol generates conflict serializable schedules that are also recoverable.
II. Timestamp-ordering concurrency control protocol with Thomas Write Rule can generate view serializable schedules that are not conflict serializable.
Which of the above statements is/are TRUE?
A | Both I and II |
B | Neither I nor II |
C | II only |
D | I only |
In strict 2PL, a transaction T does not release any of its exclusive (write) locks until after it commits or aborts.
Hence, no other transaction can read or write an item that is written by T unless T has committed, leading to a strict schedule for recoverability.
(Ref: Fundamentals of Database Systems by Elmasri and Navathe, 7e Pg. No. 789)
By ignoring the write, Thomas write rule allows schedules that are not conflict serializable but are nevertheless correct.
Those non-conflict-serializable schedules allowed satisfy the definition of view serializable schedules.
(Ref: Database System Concepts by Silberschatch, Korth and Sudarshan, 6e Pg No. 686)
Question 24 |

How many tuples will be returned by the following relational algebra query?
∏x(P.Y=R.Y ∧ R.V=V2)(P × R)) - ∏x(Q.Y=R.Y ∧ Q.T>2)(Q × R))
A | 0 |
B | 1 |
C | 2 |
D | 3 |
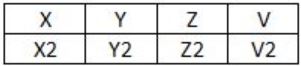
∏x(σ(P.Y = R.Y ∧ R.V = V2)(P × R))
σ(Q.Y = R.Y ∧ Q.T>2)(Q × R)
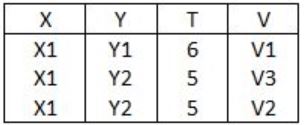 ∏x(σ(Q.Y = R.Y ∧ Q.T>2)(Q × R))
∏x(σ(Q.Y = R.Y ∧ Q.T>2)(Q × R))
∏x(σ(P.Y = R.Y ∧ R.V = V2)(P × R)) - ∏x(σ(Q.Y = R.Y ∧ Q.T>2)(Q × R))
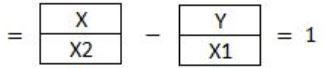
Question 25 |
A relational database contains two tables Student and Performance as shown below:
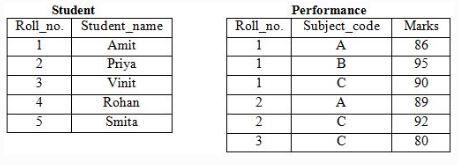
The primary key of the Student table is Roll_no. For the Performance table, the columns Roll_no. and Subject_code together from the primary key. Consider the SQL query given below:
SELECT S.Student_name, sum (P.Marks)
FROM Student S, Performance P
WHERE P.Marks > 84
GROUP BY S.Student_name;
The number of rows returned by the above SQL query is _____.
A | 0 |
B | 9 |
C | 7 |
D | 5 |
SQL> SELECT S.Student_name,sum(P.Marks)
2 FROM Student S,Performance P
3 WHERE P.Marks>84
4 GROUP BY S.Student_name;
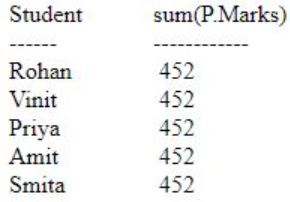
Question 26 |
Let the set of functional dependencies F = {QR → S, R → P, S → Q} hold on a relation schema X = (PQRS). X is not in BCNF. Suppose X is decomposed into two schemas Y and Z, where Y = (PR) and Z = (QRS).
Consider the two statements given below.
-
- I. Both Y and Z are in BCNF
- II. Decomposition of X into Y and Z is dependency preserving and lossless
Which of the above statements is/are correct?
A | I only |
B | Neither I nor II |
C | II only |
D | Both I and II |
R → P
R+ = RP
* In R → P, 'R' is a super key. So, Y is in BCNF.
Z = (QRS)
QR → S
S → Q
CK's = QR, RS
* In, S → Q, 'S' is not a super key. So, Z is not in BCNF.
* Y is in BCNF and Z is not in BCNF.
* 'R' is common attribute in the relations Y and Z. and R is candidate key for Y. So, the decomposition is lossless.
* The FD, R → P is applicable on Y and QR → S, S → Q are applicablein 2.
So, the decomposition is dependency preserving.
* Hence, Statement II is correct.
Question 27 |
For a database relation R(a,b,c,d), where the domains a, b, c, d include only atomic values, only the following functional dependencies and those that can be inferred from them hold:
a → c b → d
This relation is
A | in first normal form but not in second normal form |
B | in second normal form but not in third normal form |
C | in third normal form |
D | None of the above |
Since all a, b, c, d are atomic. So the relation is in 1NF.
Checking the FD's
a → c
b → d
We can see that there is partial dependencies. So it is not 2NF.
So answer is option (A).
Question 28 |
Let R(a,b,c) and S(d,e,f) be two relations in which d is the foreign key of S that refers to the primary key of R. Consider the following four operations R and S
(a) Insert into R (b) Insert into S (c) Delete from R (d) Delete from S
Which of the following can cause violation of the referential integrity constraint above?
A | None of (a), (b), (c) or (d) can cause its violation |
B | All of (a), (b), (c) and (d) can cause its violation |
C | Both (a) and (d) can cause its violation |
D | Both (b) and (c) can cause its violation |

Here 'd' is the foreign key of S and let 'a' is the primary key of R.
(A) Insertion into R: will cause no violation.
(B) Insertion into S: may cause violation because there may not be entry of the tuple in relation R. Example entry of 〈S4, __, __〉 is not allowed.
(C) Delete from R: may cause violation. For example, deletion of tuple 〈S2, __, __〉 will cause violation as there is entry of S2 in the foreign key table.
(D) Delete from S: will cause no violation as it does not result inconsistency.
Question 29 |
Given two union compatible relations R1(A,B) and R2(C,D), what is the result of the operation R1A = CAB = DR2?
A | R1 ∪ R2 |
B | R1 × R2 |
C | R1 - R2 |
D | R1 ∩ R2 |
Question 30 |
Which normal form is considered adequate for normal relational database design?
A | 2 NF |
B | 5 NF |
C | 4 NF |
D | 3 NF |
Question 31 |
There are 5 records in a database.

There is an index file associated with this and it contain the values 1, 3, 2, 5 and 4. Which one of the fields is the index built form?
A | Age |
B | Name |
C | Occupation |
D | Category |
Question 32 |
Which of the following query transformations (i.e. replacing the l.h.s. expression by the r.h.s. expression) is incorrect? R1 and R2 are relations, C1, C2 are selection conditions and A1, A2 are attributes of R1?
A | σC1(σC1(R1)) → σC2(σC2(R1)) |
B | σC1(σA1(R1)) → σA1(σC1(R1)) |
C | σC1(R1 ∪ R2) → σC1(R1) ∪ σC1 |
D | πA1(σC1(R1)) → σC1(σA1(R1)) |
Question 33 |
(a) Suppose we have a database consisting of the following three relations.
FREQUENTS(student, parlor) giving the parlors each student visits.
SERVES(parlor, ice-cream) indicating what kind of ice-creams each parlor serves.
LIKES(student, ice-cream) indicating what ice-creams each parlor serves.
(Assuming that each student likes at least one ice-cream and frequents at least one parlor)
Express the following in SQL:
Print the students that frequent at least one parlor that serves some ice-cream that they like.
(b) In a computer system where the 'best-fit' algorithm is used for allocating 'jobs' to 'memory partitions', the following situation was encountered:

When will the 20K job complete? Note - This question was subjective type.
A | Theory Explanation. |
Question 34 |
(a) Four jobs are waiting to be run. Their expected run times are 6, 3, 5 and x. In what order should they be run to minimize the average response time?
(b) Write a concurrent program using par begin - par end to represent the precedence graph shown below.

A | Theory Explanation. |
Question 35 |
Consider the following database relations containing the attributes
Book_id Subject_Category_of_book Name_of_Author Nationality_of_Author with Book_id as the Primary Key.
(a) What is the highest normal form satisfied by this relation?
(b) Suppose the attributes Book_title and Author_address are added to the relation, and the primary key is changed to (Name_of_Author, Book_Title), what will be the highest normal form satisfied by the relation?
A | Theory Explanation. |
Question 36 |
Consider the following relational database schemes:
COURSES(Cno, name) PRE-REQ(Cno, pre_Cno) COMPLETED(student_no, Cno)
COURSES give the number and the name of all the available courses.
PRE-REQ gives the information about which course are pre-requisites for a given course.
COMPLETED indicates what courses have been completed by students.
Express the following using relational algebra:
List all the courses for which a student with student_no 2310 has completed all the pre-requisites.
A | Theory Explanation. |
Question 37 |
Consider the join of a relation R with a relation S. If R has m tuples and S has n tuples then the maximum and minimum sizes of the join respectively are
A | m + n and 0 |
B | mn and 0 |
C | m + n and |m – n| |
D | mn and m + n |
Suppose there is no common attribute in R and S due to which natural join will act as cross product. So then in cross product total no. of tuples will be mn.
For minimum:
Suppose there is common attribute in R and S, but none of the row of R matches with rows of S then minimum no. of tuples will be 0.
Question 38 |
The relational algebra expression equivalent to the following tuple calculus expression:
{t| t ∈ r ∧(t[A] = 10 ∧ t[B] = 20)} isA | σ(A=10∨B=20) (r) |
B | σ(A=10) (r) ∪ σ(B=20) (r) |
C | σ(A=10) (r) ∩ σ(B=20) (r) |
D | σ(A=10) (r) - σ(B=20) (r) |
σ(A=10) (r) ∩ σ(B=20) (r)
Question 39 |
Let R = (A, B, C, D, E, F) be a relation scheme with the following dependencies: C→F, E→A, EC→D, A→B. Which of the following is a key of R?
A | CD |
B | EC |
C | AE |
D | AC |
A) (CD)+ = cdf
Not a key.
B) (EC)+ = ecdabf
Yes, it is a key.
C) (AE)+ = aeb
Not a key. D) (AC)+ = abcf
Not a key.
Question 40 |
Which of the following is correct?
A | B-trees are for storing data on disk and B+ trees are for main memory. |
B | Range queries are faster on B* trees. |
C | B-trees are for primary indexes and B* trees are for secondary indexes. |
D | The height of a B* tree is independent of the number of records. |
Question 41 |
1 Read A
2 Read B
3 Write A
4 Read A
5 Write A
6 Write B
7 Read B
8 Write B
A | This schedule is serialized and can occur in a scheme using 2PL protocol |
B | This schedule is serializable but cannot occur in a scheme using 2PL protocol |
C | This schedule is not serialiable but can occur in a scheme using 2PL protocol |
D | This schedule is not seralisable and cannot occur in a scheme using 2PL protocol. |
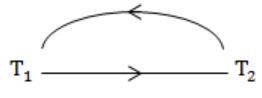
Since cycle exist so not conflict serializable.
And we know that if the schedule is not serializable then it is not 2PL.
Hence correct option is (D).
Question 42 |
Consider the schema R = (S T U V) and the dependencies S → T, T → U, U → V and V → S. Let R = (R1 and R2) be a decomposition such that R1 ∩ R2 ≠ ∅ . The decomposition is
A | not in 2NF |
B | in 2NF but not 3NF |
C | in 3NF but not in 2NF |
D | in both 2NF and 3NF |
And since every attribute is key so the decomposed relation will be in BCNF and hence in 3NF.
Question 43 |
Consider the circuit shown below. In a certain steady state, the line Y is at '1'. What are the possible values of A, B and C in this state?

A | A = 0, B = 0, C = 1 |
B | A = 0, B = 1, C = 1 |
C | A = 1, B = 0, C = 1 |
D | A = 1, B = 1, C = 1 |
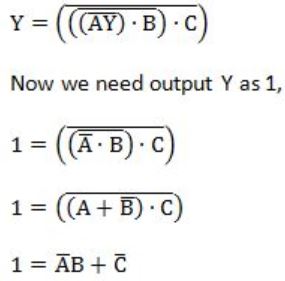
So the above equation is satisfied if either C=0 or A=0 and B=1.
Hence, Option (B) is correct.
Question 44 |
Which of the following sets of component(s) is/are sufficient to implement any arbitrary Boolean function?
A | XOR gates, NOT gates |
B | 2 to 1 multiplexors |
C | AND gates, XOR gates |
D | Three-input gates that output (A⋅B) + C for the inputs A⋅B and C |
E | Both B and C |
(B) 2 to 1 multiplexors is functionally complete.
(C) XOR gate can be used to make a NOT gate. So, (AND, NOT) is functionally complete.
(D) With given gates and inputs NOT gate cannot be derived.
Hence, not complete.
Question 45 |
Which of the following is/are correct?
A | An SQL query automatically eliminates duplicates |
B | An SQL query will not work if there are no indexes on the relations |
C | SQL permits attribute names to be repeated in the same relation |
D | None of the above |
→ If there are no indexes on the relation SQL, then also it works.
→ SQL does not permit 2 attributes to have same name in a relation.
Question 46 |
Consider a B-tree with degree m, that is, the number of children, c, of any internal node (except the root) is such that m ≤ c ≤ 2m-1. Derive the maximum and minimum number of records in the leaf nodes for such a B-tree with height h, h≥1. (Assume that the root of a tree is at height 0.)
A | Theory Explanation. |
Question 47 |
Consider the set of relations
EMP(Employee-no, Dept-no, Employee-name, Salary) DEPT(Dept-no, Dept-name, Location)
Write an SQL query to:
(a) Find all employee names who work in departments located at "Calcutta" and whose salary is greater than Rs. 50,000.
(b) Calculate, for each department number, the number of employees with a salary greater than Rs. 100,000.
A | Theory Explanation. |
Question 48 |
B+-trees are preferred to binary trees in databases because
A | Disk capacities are greater than memory capacities |
B | Disk access is much slower than memory access |
C | Disk data transfer rates are much less than memory data transfer rates |
D | Disks are more reliable than memory |
Question 49 |
Given the relations
employee (name, salary, deptno) and department (deptno, deptname, address)
Which of the following queries cannot be expressed using the basic relational algebra operations (σ, π, ×, ⋈, ∪, ∩, -)?
A | Department address of every employee |
B | Employees whose name is the same as their department name |
C | The sum of all employees’ salaries |
D | All employees of a given department |
Question 50 |
Given the following relation instance.
x y z
1 4 2
1 5 3
1 6 3
3 2 2
Which of the following functional dependencies are satisfied by the instance?
A | XY → Z and Z → Y |
B | YZ → X and Y → Z |
C | YZ → X and X → Z |
D | XZ → Y and Y → X |
If for t1[A] = t2[A] then t1[Y] = t2[Y].
