Programming
Question 1 |
int SimpleFunction (int Y[], int n, int x)
{
int total = Y[0], loopIndex;
for (loopIndex = 1; loopIndex <= n - 1; loopIndex++)
total = x * total + Y[loopIndex]
return total;
}
Let Z be an array of 10 elements with Z[i]=1, for all i such that 0 ≤ i ≤ 9. The value returned by SimpleFunction(Z, 10, 2) is _______
A | 1023 |
n=10,x=2
Initial total value is 1 => total=1.
For loop will execute 9 times.
loopindex=1, 1<=9 condition is true then
total = x * total + Y[loopIndex]= 2*1+Y[1]=2+1=3
loopindex=2, 2<=9 condition is true then
total=2*3+Y[2]=6+1=7
loopindex=3, 3<=9 condition is true then
total=2*7+Y[3]=14+1 =15
loopindex=4, 4<=9 condition is true then
total= 2*15+Y[4]=30+1=31
loopindex=5, 5<=9 condition is true then
total=2*31+Y[5]=62+1=63
loopindex=6, 6<=9 condition is true then
total=2*63+Y[6]=126+1=127
loopindex=7, 7<=9 condition is true then
Total =2*127+Y[7]=254+1=255
loopindex=8, 8<=9 condition is true then
total=2*255+Y[8]=510+1=511
loopindex=9, 9<=9 condition is true then
total=2*511+Y[9]=1022+1=1023
loopindex=10, 10<=9 condition is false then
Total value is returned which is 1023.
You can also write generalized formulae 210-1=1023
Question 2 |
# include <stdio.h>
int main()
{
int i, j, count;
count = 0;
i = 0;
for (j = -3; j <= 3; j++)
{
if ((j >= 0) && (i++))
count = count + j;
}
count = count + i;
printf(“%d”, count);
return 0;
}
Which one of the following options is correct?
A | The program will compile successfully and output 13 when executed. |
B | The program will compile successfully and output 10 when executed. |
C | The program will compile successfully and output 8 when executed. |
D | The program will not compile successfully. |
Input: count=0 , i=0 and j=-3
For(j = -3; j <= 3; j++) → Condition TRUE then enters into the loop.
if((j >= 0) && (i++)) → Condition fails because they are given logical AND.
So, we are not entering the “if” condition and come out of the loop. The count and “i” values remain “0”.
For(j = -2; j <= 3; j++) → Condition TRUE then enters into the loop.
if((j >= 0) && (i++)) → Condition fails because they are given logical AND.
So, we are not entering the “if” condition and come out of the loop. The count and “i” values remain “0”.
For(j = -1; j <= 3; j++) → Condition TRUE then enters into the loop.
if((j >= 0) && (i++)) → Condition fails because they are given logical AND.
So, we are not entering the “if” condition and come out of the loop. The count and “i” values remain “0”.
For(j = 0; j <= 3; j++) → Condition TRUE then enters into the loop.
if((j >= 0) && (i++)) → Condition TRUE then enters into the loop.
count=0+0 → Count=0
For(j = 1; j <= 3; j++) → Condition TRUE then enters into the loop.
if((j >= 0) && (i++)) → Condition TRUE then enters into the loop.
count=0+1 → Count=1
For(j = 2; j <= 3; j++) → Condition TRUE then enters into the loop.
if((j >= 0) && (i++)) → Condition TRUE then enters into the loop.
count=1+2 → Count=3
For(j = 3; j <= 3; j++) → Condition TRUE then enters into the loop.
if((j >= 0) && (i++)) → Condition TRUE then enters into the loop.
count=3+3 → Count=6
For(j = 4; j <= 3; j++) → Condition FALSE we are not entering the loop.
count=6+4 → We are given a condition as a post increment. So, “i” updates the next instruction.
The above code segment executes successfully and will print value=10.
Question 3 |
Program PARAM (input, output);
var m, n : integer;
procedure P (var, x, y : integer);
var m : integer;
begin
m : = 1;
x : = y + 1
end;
procedure Q (x:integer; vary : integer);
begin
x:=y+1;
end;
begin
m:=0; P(m,m); write (m);
n:=0; Q(n*1,n); write (n)
end
The value of m, output by the program PARAM is:
A | 1, because m is a local variable in P |
B | 0, because m is the actual parameter that corresponds to the formal parameter in p
|
C | 0, because both x and y are just reference to m, and y has the value 0 |
D | 1, because both x and y are just references to m which gets modified in procedure P |
E | none of the above |
Question 4 |
Program PARAM (input, output);
var m, n : integer;
procedure P (var, x, y : integer);
var m : integer;
begin
m : = 1;
x : = y + 1
end;
procedure Q (x:integer; vary : integer);
begin
x:=y+1;
end;
begin
m:=0; P(m,m); write (m);
n:=0; Q(n*1,n); write (n)
end
The value of n, output by the program PARAM is:
A | 0, because n is the actual parameter corresponding to x in procedure Q. |
B | 0, because n is the actual parameter to y in procedure Q. |
C | 1, because n is the actual parameter corresponding to x in procedure Q. |
D | 1, because n is the actual parameter corresponding to y in procedure Q. |
E | none of the above |
Question 5 |
Program PARAM (input, output);
var m, n : integer;
procedure P (var, x, y : integer);
var m : integer;
begin
m : = 1;
x : = y + 1
end;
procedure Q (x:integer; vary : integer);
begin
x:=y+1;
end;
begin
m:=0; P(m,m); write (m);
n:=0; Q(n*1,n); write (n)
end
What is the scope of m declared in the main program?
A | PARAM, P, Q |
B | PARAM, P |
C | PARAM, Q |
D | P, Q |
E | none of the above |
Question 6 |
What does the following code do?
var a, b : integer;
begin
a:=a+b;
b:=a-b;
a:=a-b
end; A | exchanges a and b |
B | doubles a and stores in b |
C | doubles b and stores in a |
D | leaves a and b unchanged |
E | none of the above |
Let us consider a=5; b=2
a := a+b = 5+2 = 7
b := a-b = 7-2 = 5
a := a-b = 7-5 = 2
O/P: a=2; b=5
Question 7 |
The following Pascal program segments finds the largest number in a two-dimensional integer array A[0...n-1,0...n-1] using a single loop. Fill up the boxes to complete the program and write against ![]() in your answer book. Assume that max is a variable to store the largest value and i,j are the indices to the array.
in your answer book. Assume that max is a variable to store the largest value and i,j are the indices to the array.
begin
max:= 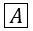 , i:=0,j:=0;
while
, i:=0,j:=0;
while 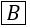 do
begin
if A[i,j]>max then max:=A[i,j]
if
do
begin
if A[i,j]>max then max:=A[i,j]
if  then j:=j+1
else begin
j:=0;
i:=
then j:=j+1
else begin
j:=0;
i:= 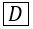 end
end
end.
end
end
end.A | Theory Explanation. |
Question 8 |
What function of x, n is computed by this program?
Function what (x, n:integer): integer:
Var
value : integer;
begin
value:=1
if n>0 then
begin
if n mod 2 = 1 then
value:=value*x;
value:=value*what(x*x, n div 2);
end;
what:value
end; A | Theory Explanation. |
Question 9 |
Consider the program below:
Program main;
var r:integer;
procedure two;
begin write (r) end;
procedure one;
var r:integer;
begin r:=5 two; end
begin r:=2;
two; one; two;
end.
What is printed by the above program if
(i) Static scoping is assumed for all variables;
(ii) Dynamic scoping is assumed for all variables.
Give reasons for your answer.
A | Theory Explanation. |
Question 10 |
An array a contains n integers in non-decreasing order, A[1] ≤ A[2] ≤ ... ≤ A[n]. Describe, using Pascal like pseudo code, a linear time algorithm to find i, j, such that A[i] + A[j] = a given integer M, if such i, j exist.
A | Theory Explanation. |
Question 11 |
(a) Draw a precedence graph for the following sequential code. The statements are numbered from S1 to S6
S1 read n S2 i:=1 S3 if i>n goto next S4 a(i):=i+1 S5 i:=i+1 S6 next : Write a(i)
(b) Can this graph be converted to a concurrent program using parbegin-parend construct only?
A | Theory Explanation. |
Question 12 |
In the following Pascal program segment, what is the value of X after the execution of the program segment?
X:=-10; Y:=20;
If X > Y then if X < 0 then X:=abs(X) else X:=2*X;
A | 10 |
B | -20 |
C | -10 |
D | None |
X = -10
Question 13 |
Which of the following strings can definitely be said to be tokens without looking at the next input character while compiling a Pascal program?
I. begin II. program III. <>
A | I |
B | II |
C | III |
D | All of the above |
Question 14 |
Assume that X and Y are non-zero positive integers. What does the following Pascal program segment do?
while X <>Y do
if X > Y then
X := X – Y
else
Y := Y – X;
write(X);
A | Computes the LCM of two numbers |
B | Divides the larger number by the smaller number |
C | Computes the GCD of two numbers |
D | None of the above |
1st pass : X=3 and Y=2
2nd pass : X=1 and Y=2
3rd pass : X=1 and Y=1
Write(X), which writes 1. Which is nothing but GCD of 3 & 5.
Question 15 |
What is the value of X printed by the following program?
program COMPUTE (input, output);
var
X:integer;
procedure FIND (X:real);
begin
X:=sqrt(X);
end;
begin
X:=2
Find(X)
Writeln(X)
end A | 2 |
B | √2 |
C | Run time error |
D | None of the above |
X in the procedure FIND is a local variable. No change will be reflected in global variable X.
Question 16 |
A variant record in Pascal is defined by
type varirec = record
number : integer;
case (var1,var2) of
var1: (x,y : integer);
var2: (p.q.: real)
end
end
Suppose an array of 100 records was declared on a machine which uses 4 bytes for an integer and 8 bytes for a real. How much space would the compiler have to reserve for the array?
A | 2800 |
B | 2400 |
C | 2000 |
D | 1200 |
Question 17 |
Consider the following high level program segment. Give the contents of the memory locations for variables W, X, Y and Z after the execution of the program segment. The values of the variables A and B are 5 CH and 92H, respectively. Also indicate error conditions if any.
var
A, B, W, X, Y :unsigned byte;
Z :unsigned integer, (each integer is represented by two bytes)
begin
X :=A+B
Y :=abs(bA-b);
W :=A-B
Z :=A*B
End; A | Theory Explanation. |
Question 18 |
(a) Consider the following Pascal function where A and B are non-zero positive integers. What is the value of GET(3,2)?
function GET(A,B:integer);integer;
begin
if B = 0 then
GET:=1
else if A < B then
GET:=0
else
GET:=GET(A-1,B)+GET(A-1,B-1)
end ;
(b) The Pascal procedure given for computing the transpose of an N × N (N>1) matrix A of integers has an error. Find the error and correct it.
Assume that the following declaration are made in the main program
const
MAXSIZE=20;
type
INTARR=array [1.,MAXSIZE,1..MAXSIZE] of integer;
Procedure TRANSPOSE (var A: INTARR; N : integer);
var
I, J, TMP, integer;
begin
for I:=1 to NO – 1 do
for J:=1 to N do
begin
TMP: = A[I,J];
A[I,J]:=A[J,I];
A(J,I):=TMP
end
end; A | Theory Explanation. |
Question 19 |
(a) Using the scope rules of Pascal determine the declaration that apply to each occurrence of the names A and B in the following program segment.
procedure T(U, V, X, Y: integer);
var
A: record
A, B : integer
end;
B: record
B, A : integer
end;
begin
with A do
begin
A:=4;
B:=V
end;
with B do
begin
A:=X;
B:=Y
end
end;
(b) Find the lexical errors in the following Pascal statement:
if A > 1, then B = 2.5A else read (C);
A | Theory Explanation. |
Question 20 |
The following is an incomplete Pascal function to convert a given decimal integer (in the range -8 to +7) into a binary integer in 2’s complement representation. Determine the expression A, B, C that complete program.
function TWOSCOMP (N:integer):integer;
var
RAM, EXPONENT:integer;
BINARY :integer;
begin
if(N>=-8) and (N<=+7) then
begin
if N<0 then
N : = A;
BINARY:=0;
EXPONENT:=1;
while N<>0 do
begin
REM:=N mod 2;
BINARY:=BINARY + B*EXPONENT;
EXPONENT:=EXPONENT*10;
N := C
end
TWOSCOMP:=BINARY
end
end;
A | Theory Explanation. |
Question 21 |
Consider the following C functions.
int fun1 (int n) { int fun2 (int n) {
static int i = 0; static int i = 0;
if (n > 0) { if (n > 0) {
++i; i = i + fun1 (n);
fun1 (n-1); fun2 (n-1);
} }
return (i); return (i);
} }
The return value of fun2 (5) is _______.
A | 55 |
int fun1(int n) {
printf("--fun1 call--\n");
static int i = 0;
if(n>0){
++i;
printf("fun1(%d-1)\n",n);
fun1(n-1);
}
printf("fun1(%d)= %d\n",n, i);
return(i);
}
int fun2(int n) {
printf("\n******* fun2 call ********\n");
static int i = 0;
if(n>0){
printf("%d + fun1(%d)\n", i,n);
i=i+fun1(n);
fun2(n-1);
}
printf("fun2(%d)= %d\n",n, i);
return(i);
}
void main()
{
printf("final = %d\n", fun2(5));
}
Check step by step hand run of the code to understand the recursion:
******* fun2 call ********
0 + fun1(5)
--fun1 call--
fun1(5-1)
--fun1 call--
fun1(4-1)
--fun1 call--
fun1(3-1)
--fun1 call--
fun1(2-1)
--fun1 call--
fun1(1-1)
--fun1 call--
fun1(0)= 5
fun1(1)= 5
fun1(2)= 5
fun1(3)= 5
fun1(4)= 5
fun1(5)= 5
******* fun2 call ********
5 + fun1(4)
--fun1 call--
fun1(4-1)
--fun1 call--
fun1(3-1)
--fun1 call--
fun1(2-1)
--fun1 call--
fun1(1-1)
--fun1 call--
fun1(0)= 9
fun1(1)= 9
fun1(2)= 9
fun1(3)= 9
fun1(4)= 9
******* fun2 call ********
14 + fun1(3)
--fun1 call--
fun1(3-1)
--fun1 call--
fun1(2-1)
--fun1 call--
fun1(1-1)
--fun1 call--
fun1(0)= 12
fun1(1)= 12
fun1(2)= 12
fun1(3)= 12
******* fun2 call ********
26 + fun1(2)
--fun1 call--
fun1(2-1)
--fun1 call--
fun1(1-1)
--fun1 call--
fun1(0)= 14
fun1(1)= 14
fun1(2)= 14
******* fun2 call ********
40 + fun1(1)
--fun1 call--
fun1(1-1)
--fun1 call--
fun1(0)= 15
fun1(1)= 15
******* fun2 call ********
fun2(0)= 55
fun2(1)= 55
fun2(2)= 55
fun2(3)= 55
fun2(4)= 55
fun2(5)= 55
final = 55
Question 22 |
int tob (int b, int* arr) {
int i;
for (i=0; b>0; i++) {
if (b%2) arr [i] = 1;
else arr [i] = 0;
b = b/2;
}
return (i);
}
int pp (int a, int b) {
int arr [20];
int i, tot = 1, ex, len;
ex = a;
len = tob (b,arr);
for (i=0; i
tot = tot * ex;
ex = ex * ex;
}
return (tot);
}
The value returned by pp(3,4) is ________.
A | 81 |
a=3,b=4
tot=1
ex=a=3
len=tob(b,arr) which is 3
[
tob(4,arr)==>
b=4
b%2 =4%2=0 Condition is false then arr[0]=0
=> b=b/2 =4/2 =2
b=2
b%2 =2%2=0 condition is false then arr[1]=0
=>b=b/2=2/2=1
b=1
then b%2=1%2 condition is true then arr[2]=1
=>b=b/2=1/2=0
The i value is 3 [length is 3]
]
i=0,
arr[0] ==1 condition is false
ex=3*3=9
i=1
arr[1]==1 condition is false
then
ex=9*9=81
i=2
then arr[2]==1 condition is true
tot=tot*ex=1*81=81
ex=81*81
Finally it returns tot value which 81.
Question 23 |
Given the following Pascal-like program segment
Procedure A;
x,y: integer;
Procedure B;
x,z: real
S1
end B;
Procedure C;
i: integer;
S2
end C;
end A;
The variables accessible in S1 and S2 are
A | x or A, y, x of B and z in S1 and x of B, y and i in S2 |
B | x or B, y and z in S1 and x of B, i and z in S2 |
C | x or B, z and y in S1 and x of A, i and y in S2 |
D | None of the above |
Question 24 |
What value would the following function return for the input x=95?
Function fun (x:integer):integer;
Begin
If x > 100 then fun = x - 10
Else fun = fun(fun(x + 11))
End; A | 89 |
B | 90 |
C | 91 |
D | 92 |
fun(95) = fun(fun(106))
= fun(96)
= fun(fun(107))
= fun(97)
= fun(fun(108))
= fun(98)
= fun(fun(109))
= fun(99)
= fun(110)
= fun(100)
= fun(fun(111))
= fun(101)
= 91
Question 25 |
What is the result of the following program?
program side-effect (input, output);
var x, result: integer;
function f (var x:integer):integer;
begin
x:x+1;f:=x;
end;
begin
x:=5;
result:=f(x)*f(x);
writeln(result);
end; A | 5 |
B | 25 |
C | 36 |
D | 42 |
If it is call by value then answer is 36.
Question 26 |
Given the programming constructs (i) assignment (ii) for loops where the loop parameter cannot be changed within the loop (iii) if-then-else (iv) forward go to (v) arbitrary go to (vi) non-recursive procedure call (vii) recursive procedure/function call (viii) repeat loop, which constructs will you not include in a programming language such that it should be possible to program the terminates (i.e., halting) function in the same programming language.
A | (ii), (iii), (iv) |
B | (v), (vii), (viii) |
C | (vi), (vii), (viii) |
D | (iii), (vii), (viii) |
Question 27 |
Consider the following C function definition.
int Trial (int a, int b, int c)
{
if ((a >= b) && (c < b) return b;
else if (a >= b) return Trial(a, c, b);
else return Trial(b, a, c);
}
The function Trial:
A | Finds the maximum of a, b, and c |
B | Finds the minimum of a, b and c |
C | Finds the middle number of a, b, c |
D | None of the above |
Question 28 |
Suppose we have a function HALTS which when applied to any arbitrary function f and its arguments will say TRUE if function f terminates for those arguments and FALSE otherwise. Example, Given the following function definition.
FACTORIAL (N) = IF(N=0) THEN 1 ELSE N*FACTORIAL (N-1)
Then HALTS(FACTORIAL 4) = TRUE and HATS(FACTORIAL - 5) = FALSE
Let us define the function FUNNY(f) = IF HALTS(ff) THEN not(ff) ELSE TRUE
(a) Show that FUNNY terminates for all functions f.
(b) Use (a) to prove (by contradiction) that it is not possible to have a function like HALTS which for arbitrary functions and inputs says whether it will terminate on that input or not.
A | Theory Explanation. |
Question 29 |
What will be the output of the following program assuming that parameter passing is
- (i) call by value
(ii) call by reference
(iii) call by copy restore
procedure P{x, y, z};
begin y:y+1; z: x+x end;
begin
a:= b:= 3;
P(a+b, a, a);
Print(a)
end. A | Theory Explanation. |
Question 30 |
Consider the following pascal program skeleton:
program sort(...); var a,x,...;
procedure readarray;
var i,....;
begin
...:=a...
end;
procedure exchange(...);
begin
...:=a...
...:=x...
end;
procedure qsort(...);
var k,v,...;
function partition (...)...;
var i,j,...;
begin
...:=a...
...:=v...
end;
begin
.
.
end;
begin
.
.
end;
Assume that at a given point in time during program execution, following procedures are active: sort, qsort(1,9), qsort(1.3), partition(1,3), exchange(1,3).
Show snapshots of the runtime stack with access links after each of the activations.
A | Theory Explanation. |
Question 31 |
The following C declarations
struct node
{
int i;
float j;
};
struct node *s[10];
define s to be
A | An array, each element of which is a pointer to a structure of type node |
B | A structure of 2 fields, each field being a pointer to an array of 10 elements |
C | A structure of 3 fields: an integer, a float, and an array of 10 elements |
D | An array, each element of which is a structure of type node |
Question 32 |
The most appropriate matching for the following pairs
X: m=malloc(5); m= NULL; 1: using dangling pointers
Y: free(n); n->value=5; 2: using uninitialized pointers
Z: char *p; *p = ’a’; 3. lost memory
is:
A | X – 1 Y – 3 Z – 2 |
B | X – 2 Y – 1 Z – 3 |
C | X – 3 Y – 2 Z – 1 |
D | X – 3 Y – 1 Z – 2 |
Y → n is pointer to invalid memory, a making it as a dangling pointer.
Z → p is not initialized.
p = malloc (size of(char))p = malloc (size of(char)); should have been used before assigning 'aa' to ∗p.
Question 33 |
Aliasing in the context of programming languages refers to
A | multiple variables having the same memory location |
B | multiple variables having the same value |
C | multiple variables having the same identifier |
D | multiple uses of the same variable |
Question 34 |
Consider the following C declaration
struct {
short s [5]
union {
float y;
long z;
} u;
} t;
Assume that objects of the type short, float and long occupy 2 bytes, 4 bytes and 8 bytes, respectively. The memory requirement for variable t, ignoring alignment considerations, is
A | 22 bytes |
B | 14 bytes |
C | 18 bytes |
D | 10 bytes |
max[float, long] = max [4, 8] = 8
Total = short[5] + max[float,long] = 10 + 8 = 18
Question 35 |
The value of j at the end of the execution of the following C program.
int incr(int i)
{
static int count = 0;
count = count + i;
return (count);
}
main()
{
int i,j;
for (i = 0; i <= 4; i++)
j = incr(i);
}
is
A | 10 |
B | 4 |
C | 6 |
D | 7 |
i=1; count=1
i=2; count=3
i=3; count=6
i=4; count=10
It return count value is 10.
Question 36 |
Consider the following program is pseudo-Pascal syntax.
program main;
var x: integer;
procedure Q [z:integer);
begin
z: z + x;
writeln(z)
end;
procedure P (y:integer);
var x: integer;
begin
x: y + 2;
Q(x);
writeln(x)
end;
begin
x:=5;
P(x);
Q(x);
writeln(x)
end.
What is the output of the program, when
(a) The parameter passing mechanism is call-by-value and the scope rule is static scooping?
(b) The parameter passing mechanism is call-by-reference and the scope rule is dynamic scooping?
A | Theory Explanation is given below. |
Question 37 |
What is printed by the print statements in the program P1 assuming call by reference parameter passing?
Program P1()
{
x = 10;
y = 3;
func1(y,x,x);
print x;
print y;
}
func1(x,y,z)
{
y = y+4;
z = x+y+z;
} A | 10, 3 |
B | 31, 3 |
C | 27, 7 |
D | None of the above |
And variable y and z of func1 points to address of variable x.
Therefore, y = y+4 ⇒ y = 10+4 = 14
and z = x+y+z ⇒ z = 14+14+3 = 31
z will be stored back in k.
Hence, x=31 and y will remain as it is (y=3).
Hence, answer is (B).
Question 38 |
Consider the following program
Program P2
var n: int:
procedure W(var x: int)
begin
x=x+1;
print x;
end
procedure D
begin
var n: int;
n=3;
W(n);
End
begin //beginP2
n=10;
D;
end
If the language has dynamic scoping and parameters are passed by reference, what will be printed by the program?
A | 10 |
B | 11 |
C | 3 |
D | None of the above |
W(n)=W(3)
Procedure W(var x; int)
begin
x = x+1 = 3+1 = 4
Print x → Print x=4
end
Question 39 |
Consider the following C program:
void abc(char*s)
{
if(s[0]==’\0’)return;
abc(s+1);
abc(s+1);
printf(“%c”,s[0]);
}
main()
{ abc(“123”)
}
(a) What will be the output of the program?
(b) If abc(s) is called with a null-terminated string s of length n characters (not
counting the null (‘\0’) character), how many characters will be printed by abc(s)?
A | Theory Explanation is given below. |
Question 40 |
In the C language
A | At most one activation record exists between the current activation record and the activation record for the main |
B | The number of activation records between the current activation record and the activation record for the main depends on the actual function calling sequence. |
C | The visibility of global variables depends on the actual function calling sequence. |
D | Recursion requires the activation record for the recursive function to be saved on a different stack before the recursive fraction can be called. |
Question 41 |
#include <stdio.h>
int counter = 0;
int calc (int a, int b) {
int c;
counter++;
if (b==3) return (a*a*a) ;
else {
c = calc (a, b/3) ;
return (c*c*c) ;
}
}
int main () {
calc (4, 81);
printf ("%d", counter) ;
}
The output of this program is ______.
A | 4 |
B | 5 |
C | 6 |
D | 7 |

Question 42 |
Consider the following C program.
#include <stdio.h>
struct Outnode {
char x, y, z ;
};
int main () {
struct Outnode p = {'1', '0', 'a'+2} ;
struct Outnode *q = &p ;
printf ("%c, %c", *((char*)q+1), *((char*)q+2)) ;
return 0 ;
}
The output of this program is
A | 0, c |
B | 0, a+2 |
C | ‘0’, ‘a+2’ |
D | ‘0’, ‘c’ |
The x variable here stores a character ‘c’ in it.
Because +2 will increment ascii value of a from 92 to 95.
Hence the structure p contains 3 character values and they are ‘1’, ‘0’, and ‘c’.
q is a pointer pointing to structure p.
Hence q is pointing to ‘1’, q+1 pointing to ‘0’ and q+2 pointing to ‘c’.
Option d cannot be correct, as though they are characters, printf will not print them in single quotes.
Question 43 |
Consider the following C program:
#include<stdio.h>
void fun1(char *s1, char *s2) {
char *tmp;
tmp = s1;
s1 = s2;
s2 = tmp;
}
void fun2(char **s2, char **s2) {
char *tmp;
tmp = *s1;
*s1 = *s2;
*s2 = tmp;
}
int main () {
char *str1 = "Hi", *str2 = "Bye";
fun1(str1, str2); printf("%s %s", str1, str2);
fun2(&str1, &str2); printf("%s %s", str1, str2);
return 0;
}
The output of the program above is
A | Hi Bye Bye Hi |
B | Hi Bye Hi Bye |
C | Bye Hi Hi Bye |
D | Bye Hi Bye Hi |
Hence, any change in the formal parameters are NOT reflected in actual parameters.
Hence, str1 points at “hi” and str2 points at “bye”.
The second call to the function ‘func2(&str1, &str2);’ is call by reference.
Hence, any change in formal parameters are reflected in actual parameters.
Hence, str1 now points at “bye” and str2 points at “hi”.
Hence answer is “hi bye bye hi”.
Question 44 |
Consider the following C code. Assume that unsigned long int type length is 64 bits.
unsigned long int fun(unsigned long int n) {
unsigned long int i, j, j=0, sum = 0;
for (i = n; i > 1; i = i/2) j++;
for ( ; j > 1; j = j/2) sum++;
return sum;
}
The value returned when we call fun with the input 240 is
A | 4 |
B | 5 |
C | 6 |
D | 40 |
Next for loop will divide j value (which is 40) by 2, each time until j>1.
j loop starts:
j=40 & sum=1
j=20 & sum=2
j=10 & sum=3
j=5 & sum=4
j=2 & sum=5
j=1 & break
So, sum = 5.
Question 45 |
Consider the following program written in pseudo-code. Assume that x and y are integers.
Count (x, y) {
if (y != 1) {
if (x != 1) {
print("*") ;
Count (x/2, y) ;
}
else {
y = y - 1 ;
Count (1024, y) ;
}
}
}
The number of times that the print statement is executed by the call Count(1024, 1024) is ______.
A | 10230 |
B | 10231 |
C | 10232 |
D | 10233 |
int count=0;
Count(x,y){
if(y!=1){
if(x!=1){
printf("*");
count = count +1;
Count(x/2,y);
}
else{
y=y-1;
Count(1024,y);
}
}
}
void main()
{
Count(1024,1024);
printf("\n%d\n",count);
}


Count ( ) is called recursively for every (y = 1023) & for every y, Count ( ) is called (x = 10) times = 1023 × 10 = 10230
Question 46 |
Consider the following PASCAL program segment:
if i mode 2 = 0 then
while i > = 0 do
begin
i:=i div 2;
if i mod 2 < > 0 do then i:=i – 1
else i:=i – 2
end
An appropriate loop-invariant for the while-loop is ______
A | PASCAL is out of syllabus. |
Question 47 |
Consider the following recursive definition of fib:
fib (n) : = if n = 0 then 1
else if n = 1 than 1
else fib (n – 1) + fib (n – 2)
The number of times fib is called (including the first call) for an evaluation of fib (7) is ___________
A | 41 |
T(n) = T(n-1) + T(n-2) + 2
T(0) = T(1) = 0 (for fib(0) and fib(1), there are no extra recursive calls)
T(2) = 2
T(3) = 4
T(4) = 8
T(5) = 14
T(6) = 24
T(7) = 40
Counting the initial call, we get
40+1 = 41
Question 48 |
Choose the correct alternatives (more than one may be correct) and write the corresponding letters only: Consider the following Pascal function:
function X (M:integer) : integer; var i:integer; begin i = 0; while i*i < M do i; =i+1 X;=i endThe function call X(N), if N is positive, will return
A | (√N) |
B | (√N)+1 |
C | [√N] |
D | [√N]+1 |
E | None of the above |
Question 49 |
Give short answers to the following questions:
(i) Convert the following Pascal statement to a single assignment statement:
if x > 5 they y:=true
else y:=false;
(ii) Convert the Pascal statement repeat S until B; into an equivalent Pascal statement that uses the while construct. (iii) Obtain the optimal binary search tree with equal probabilities for the identifier set (a1, a2, a3) = (if, stop, while)
(iv) If a finite axiom system A for a theory is complete and consistent, then is every subsystem of A complete and consistent? Explain briefly.
A | Theory Explanation. |
Question 50 |
(a) Consider the following pseudo-code
(all data items are of type integer):
Procedure P (a, b, c);
a:=2;
c:=a+b;
end {P}
begin
x:=1
y:=5;
z:=100;
P(x,x*y,z);
Write (‘x=’,x,z=’,z)
end:
Determine its output, if the parameters are passed to the procedure P by (i) value, (ii) reference and (iii) name.
(b) For the following pseudo-code, indicate the output, if
(i) static scope rules and (ii) dynamic scope rules are used
Var, a, b : integer;
Procedure P;
a:=5; b:=10
end {P};
procedure Q;
var a, b : integer;
P;
end {Q};
begin
a:=1; b:=2;
Q;
Write (‘a =’, a, ‘b=’,b)
end.
A | Theory Explanation. |
